Собственные векторы и собственные значения матрицы.

Характеристическим уравнением матрицы А = называется уравнение , т.е. .

Корни этого уравнения l₁, l₂, l₃ называются характеристическими числами матрицы А или собственными значениями матрицы А, эти числа действительные, если матрица является симметрической.Если элементы квадратной матрицы удовлетворяют условию а_ij = a_ji, то матрица называется симметрической.

Ненулевой вектор х называется собственным вектором квадратичной матрицы А, принадлежащим ее собственному значению l совпадает с множеством всех ненулевых решений системы однородных уравнений () х = 0, записанных в векторно-матричной форме.

в которой l имеет одно из значений l₁, l₂, l₃ и определитель которой в силу этого равен нулю, определяет тройку чисел соответствующую данному собственному значению который и является искомым собственным вектором.

Пример. Дана матрица 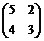. Найти собственные значения и собственные векторы.

Решение:

Составим характеристическое уравнение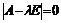

=0

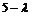()() – 8 = 0

l² - 8l + 7 = 0

l₁=7, l₂ = 1.

Находим собственный вектор, соответствующий первому собственному значению

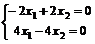; Þ х₁ = х₂ Þ - собственный вектор, соответствующий собственному числу l₁=7

Находим собственный вектор, соответствующий второму собственному значению

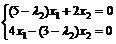; Þ 2 х₁ =- х₂ Þ х₁ = 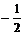х₂ Þ - собственный вектор, соответствующий собственному числу l₂ = 1

II. ВЕКТОРНАЯ АЛГЕБРА.

Различают два рода величин: скалярные и векторные.

Если некоторая величина определяется только ее число­вым значением, то ее называют скалярной. Если при определении некоторой величины для ее полной характеристики, кроме числового значения, надо знать и ее направление, то такая величина называется векторной, или век­тором. Длина вектора называется также его модулем, или абсолютной величиной. Вектор равен нулю, если его модуль равен нулю. Такой вектор называется нулевым.

Два вектора 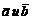называются равными, если равны их мо­дули, они параллельны и сонаправлены.

При умножении вектора на скаляр k получается вектор 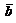модуль которого равен модулю вектора , умноженному на k. Направления векторов 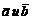совпадают, если k > 0, и они противоположны, если k < 0.

Два вектора, лежащие на параллельных прямых называются коллинеарными.

Не нашли, что искали? Воспользуйтесь поиском: