Если уравнения прямых заданы в общем виде. угол между ними определяется по формуле .

А₁х+В₁у+С₁=0,

А₂ x+В₁y+Сз=О,

угол между ними определяется по формуле .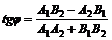

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями с угловым коэф­фициентом, то необходимое и достаточное условие их параллель­ности состоит в равенстве их угловых коэффициентов:

k₁ = k₂

б) Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

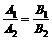
Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями с угло­вым коэффициентом, необходимое и достаточное условие их пер­пендикулярности заключается в том, что их угловые коэффициенты обратно пропорциональны

Это условие может быть записано также в виде k₁k₂ = -1

б) Если уравнения прямых заданы в общем виде, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ =0

Координаты точки пересечения двух прямых находят, решая систему уравнений

А₁х+В₁у+С₁=0,

А₂ x+В₁y+Сз=О.

Прямые пересекаются только в том случае, когда A₁A₂ - - B₁B₂ ¹ 0

Пример. Найти уравнение прямой, проходящей через две точки: (—1, 2) и (2, 1).

Решение:

По уравнению 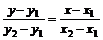, полагая в нем х₁ = - 1, y₂ = 2, x₂ = 2, y₂ =1, получим после упрощений получаем окончательно искомое уравнение в виде x + 3 y – 5 = 0

Пример. Стороны треугольника заданы уравнениями:

(AB) 2х+4у+ 1=0,

(AC) х- у+ 2=0,

(ВС) Зх+4у— 12=0.Найти координаты вершин треугольника.

Решение:

Координаты вершины А найдем, решая систему, составленную из уравнений сторон АВ и АС:

Решая систему двух линейных уравнений с двумя неизвестными, полу­чаем 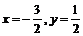. Значит, вершина А имеет координаты А= .

Координаты вершины В найдем, решая систему сторон АВ и ВС

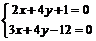
Получаем, что вершина В имеет координаты В=

Координаты вершины С найдем, решая систему сторон АС и ВС.

Получаем, что вершина С имеет координаты С=

Расстояние точки А (х₁, у₁) до прямой Ax + By + С = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

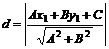
Правило. Чтобы определить расстояние от точки А (х₁, у₁) до прямой Ax + By + С = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние.

Пример. Найти расстояние от начала координат до прямой х + у —2=0.

Решение:

Не нашли, что искали? Воспользуйтесь поиском: