
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Схема текущего контроля усвоения учебного материала
Текущий контроль усвоения материала осуществляется в процессе проведения всех видов занятий. При чтении лекций усвоение материала проверяется путем постановки контрольных вопросов и проблемного изложения материала. При проведении практических работ усвоение материала контролируется проверкой знаний предусмотренных методическими указаниями по подготовке и проведению практических занятий, а также путем рейтингового контроля результатов выполнения расчетов и построений. Информация о посещении занятий и текущей успеваемости согласно графика выполнения практических работ отмечается на стенде текущей успеваемости и при проведении ежемесячной аттестации.
Итоговый контроль
1. Общие требования к вычислениям.
2. Приближенные числа, правила округления.
3. Абсолютные и относительные ошибки арифметических действий.
4. Единицы измерения дуг и углов.
5. Прямая и обратная интерполяция. Формулы Ньютона и Бесселя.
6. Точность определения натуральных значений и логарифмов тригонометрических функций.
7. Основные понятия и определения сферической геометрии и тригонометрии.
8. Сферические треугольники, их типы и свойства.
9. Основные теоремы и формулы сферической тригонометрии.
10. Дополнительные формулы для решения косоугольных сферических треугольников.
11. Решение косоугольных сферических треугольников.
12. Решение сферических треугольников при помощи таблиц.
13. Решение прямоугольных и четвертных сферических треугольников.
14. Вероятность и частота, сложение и умножение вероятностей.
15. Распределения случайных величин и их основные характеристики.
16. Классификация измерений и погрешностей.
17. Законы распределения случайных величин.
18. СКП величин подчиненных нормальному закону.
19. Случайные погрешности и их основные характеристики.
20. Методы расчета СКП, оценка точности наблюдений.
21. Систематические погрешности, их возникновение и меры по уменьшению влияния.
22. Погрешности функций измеряемых величин.
23. Математическая статистика, основные понятия.
24. Погрешности неравноточных измерений.
25. Оценка истинного значения измеряемой величины.
26. Вероятнейшее значение погрешности различных измерений и оценка его точности.
27. Доверительные интервалы и надежность.
28. Взаимозависимые погрешности и оценка корреляции между ними.
29. Расчеты коэффициента линейной корреляции и уравнения регрессии.
Типы задач
1. Преобразования угловых (дуговых) величин.
2. Работа с таблицами.
3. Решение косоугольного сферического треугольника.
4. Решение прямоугольного сферического треугольника с оценкой точности расчета одного из элементов.
5. Решение четвертного сферического треугольника с оценкой точности расчета одного из элементов.
6. Расчет СКП равноточных и неравноточных измерений с заданной точностью.
7. Расчет СКП с доверительным интервалом и заданной надёжностью.
8. Расчет коэффициента линейной корреляции и уравнения регрессии параметров.
9. Расчет коэффициента линейной корреляции и уравнения регрессии двух величин.
10. Расчет СКП высоты светила.
11. Расчет СКП навигационного параметра по его функции.
Глава 2. Математическая обработка результатов наблюдений
Работа с таблицами
Судоводители постоянно решают задачи с большим количеством расчётов для облегчения, которых используют различные вспомогательные таблицы. Поэтому штурман обязан знать принципы построения и приёмы работы с ними.
Как правило, таблица выражает определённую функциональную зависимость и содержит значения функции для ряда аргументов. Эти значения аргументов и соответствующие им значения функций называются табличными. Разность между смежными табличными значениями аргумента называются табличным шагом аргумента. Шаг аргумента выбирается таким образом, что бы изменение функции на этом промежутке, без существенных потерь в точности, можно было считать линейным. Совершенно не обязательно, что шаг аргумента во всей таблице будет постоянным.
Таблицы функций одного аргумента для большей компактности зачастую делают с двойным входом. К примеру, по вертикали (в столбце) идут целые значения аргумента, по горизонтали (в строке)– десятичные доли (возможны и другие варианты).
Таблицы функций двух аргументов имеют два входа – по строкам и столбцам. На пересечении соответствующих столбца и строки, находится табличное значение функции.
При совпадении расчётного аргумента с табличным, выборка значения функции не требует вычислений, в противном случае требуются дополнительные расчёты – интерполяция.
Интерполяцией называют отыскание промежуточных значений величины, по известным её значениям.
Разберём самый простой способ интерполяции – линейную интерполяцию. Пусть аргументу x0 соответствует значение функции y0, а ближайшему к x0 значению x1 соответствует y1. Тогда шаг таблицы h = x1 - x0, а разность соответствующих величин функции D = y1 - y0. Найдём значение функции y′ соответствующее аргументу x′, если x0<x′< x1. Найдём величину Δ x = x′ - x0, тогда 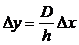 , соответственно y′ = y0 + Δ y.
, соответственно y′ = y0 + Δ y.
Стоит заметить, что величина Δ y может быть как положительной, так и отрицательной, что зависит от характера изменения функции при возрастании (убывании) аргумента.
Для примера возьмём фрагмент таблицы 5-а МТ-75(63) (Таблица 1.1).
Таблица 1.1

| D | 24о | sin | D | cosec | tg | D | ctg | sec | D | cos | |
| 8,63576 | 0’ | 9.60931 | 0.39069 | 9.64858 | 0.35142 | 0.03927 | 9.96037 | 60’ | ||||
| 1’ | 59’ | |||||||||||
| 2’ | 58’ | |||||||||||
| 3’ | 57’ | |||||||||||
| 4’ | 56’ |
В таблице приведены значения десятичных логарифмов (или их приращения до десяти) тригонометрических функций от 0о до 90о с шагом 1′. При входе сверху и слева значения от 0о до 45о, при входе снизу и справа от 45о до 90о. В первом случае обозначения функций берут в верхней строке, во втором – в нижней.
Пример 1.1
Найдём значение lg sin для 24о 2.3′.
1. Открываем таблицы на странице для целого числа градусов, в нашем случае 24о;
2. В колонке минут, расположенной под значением градусов, находим строку с ближайшим целым значением минут, в нашем случае 2′ (в случае если число градусов более 45°, вход справа и снизу, а колонка минут расположена над значением градусов в направлении снизу – вверх);
3. На пересечении найденной строки с колонкой необходимой функции, в нашем случае sin, находим значение функции – 9,60988.
4. Вычитаем найденное значение из следующего, т.е. для 3′,
9,61016-9,60988=0,000(28). Значащие цифры этой разности (пропорциональные части) приведены в колонке D. Следовательно, изменению на 0,3′ соответствует величина 0,3∙28=8,4≈(8).
5. Прибавляем к значению для 2′, 9,60988+0,0000(8)=9,60996.
Ответ: lg(sin (24о02,3′))=9.60996
Обратная интерполяция позволяет по известному значению функции получить значение аргумента. Производится в обратном порядке.
Пример 1.2
Дано: lg(tg(x)) =9,64975.
Найти x:
Путём длительных поисков в колонке функции находим её значение ближайшее к заданному 9,64960 и выбираем аргумент этого значения 24о3′.
1. Вычитаем из заданного значения найденное
9,64975-9,64960=0,000(15).
2. Делим полученную разность (последние значащие цифры) на пропорциональные части, приведённые в колонке D 15/34≈0,4 (если колонка D в Ваших таблицах почему-то отсутствует, то значение D рассчитываем сами).
3. Результат прибавляем (вычитаем) к аргументу 24о3′+0,4′=24о3,4′.
Ответ x =24о3,4′.
В некоторых случаях, например в таблицах 3-а и 3-б МТ-75, приходится интерполировать две последние значащие цифры аргумента, для этого в правой части листа приводятся таблицы пропорциональных частей.
Для примера возьмём фрагмент таблицы 3-а МТ-75 (Таблица 1.2).
Таблица 1.2
| lg a -lg b | Проп. части | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.50 | 0.11933 |
| |||||||||||||||||||||||||||||||||||||||||||||||||
Пример 1.3
Дано: lg a=9.98564, lg b=9.34407
Найти: lg (a+b)
1. Рассчитываем Аргумент Гаусса (А.Г.).
А.Г.= lg a – lg b = 9.86564 -9.34407 = 0,52157 (всегда из большего вычитаем меньший).
2. В таблице 3-а (Таблица 1.2)в первой колонке (lg a -lg b)находим первые значащие цифры 0,52.
3. В верхней строке находим следующую значащую цифру 1.
4. На пересечении найденных строки и столбца выбираем значение 0,11438 и следующее значение 0,11415.
5. Находим разность 0,11438 - 0,11415=0,000(23).
6. Берём предпоследнюю значащую цифру 5 и входим в таблицу проп. частей (строка 5, колонка 23), выбираем значение 11.5.
7. Последнюю значащую цифру 7 интерполируем в этой же таблице, как десятые предпоследней цифры. Получаем 11.5+1,6=13,1≈(13)
8. Вычитаем из значения для 0,521 (п.4) 0,11438-0,000(13)=0,11425
9. Полученное значение разности логарифмов прибавляем к большему логарифму 9,86564+0,11425=9,97989
Ответ: lg (a+b)=9,97989
Не нашли, что искали? Воспользуйтесь поиском: