Средняя квадратичная погрешность функции измеренных величин.

В практике часто бывают случаи, когда измеренные параметры входят в какую-либо расчётную формулу, причём зачастую сразу несколько параметров. Встаёт вопрос, каким образом определить СКП результата.

Предположим, что какая-либо величина z является функцией некоторого количества различных навигационных параметров x₁, x₂,…x_n,

z=f(x₁, x₂,…x_n);

каждый из которых имеет среднюю квадратичную погрешность m_xi, тогда формула для расчёта m_z будет иметь вид:

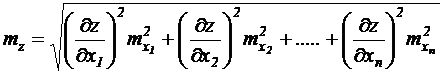(5.1)

Из общей формулы (5.1) можно вывести несколько частных имеющих более простой вид:

1) линейная функция z = Ax1 ± Bx2 ±….± Cxn, тогда

(5.2)

2) z=±Ax, тогда

(5.3)

3) линейная функция z = x1 ± x2 ±….± x, тогда

(5.4)

В общем случае по формуле (5.1) рекомендуется следующий порядок расчётов:

1. Рассчитывают по исходной формуле значение определяемой величины.

2. Рассчитывают частные производные по переменным (измеренным) величинам.

3. Преобразовывают общую формулу СКП для конкретного случая, что бы она имела рабочий вид, и в неё можно было подставлять числа.

4. В рабочую формулу подставляют исходные значения и рассчитывают СКП m_z.

Пример 5.1

Дано: Скорость судна на мерной миле определяется по формуле:

S=3кб, m_s=±0.1кб, t=2мин, m_t=±1сек

Найти: Скорость судна на и СКП скорости.

Решение:

Частные производные: и

Формула (5.1) примет вид:

Не нашли, что искали? Воспользуйтесь поиском: