Безопасность алгоритма RSA

Безопасность алгоритма RSA основана на трудоемкости разложения на множители больших чисел. Современное состояние технических средств разложения на множители таково, что число, содержащее 193 десятичных знака, факторизовано в 2005 г. Следовательно, выбираемое должно быть больше. Большинство общепринятых алгоритмов вычисления простых чисел и носят вероятностный характер.

Для работы алгоритма RSA нужны простые числа. Наиболее приемлемым является генерация случайных чисел и последующая проверка их на простоту. Существуют вероятностные тесты, определяющие с заданной степенью достоверности факт простоты числа. Возникает вопрос, что произойдет, если числа окажутся составными? Можно свести вероятность такого события до приемлемого минимума, используя тесты на простоту. Кроме того, если такое событие произойдет, это будет быстро обнаружено — шифрование и расшифрование не будут работать.

Кроме разрядности и , к ним предъявляются следующие дополнительные требования:

– числа не должны содержаться в списках известных больших простых чисел;

– они не должны быть близкими, так как иначе можно воспользоваться для факторизации N методом Ферма и решить уравнение ;

– в алгоритме RSA всегда есть эквивалентные по расшифрованию показатели степеней, например 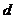и . При этом эквивалентных решений тем больше, чем больше . В лучшем случае ,
, где – нечетные числа с условием .

Чтобы исключить возможность применения методов факторизации накладывают следующее ограничение: числа не должны разлагаться в произведение маленьких простых множителей, должны содержать в качестве сомножителя хотя бы одно большое простое число. В 1978 г.

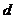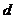Рассмотрим вопрос о выборе экспонент шифрования и рас­шифрования. Так как значения и определяют время зашифрования и расшифрования, то можно назвать ряд ситуаций, в которых желательно иметь малое значение и . Например, при использовании системы RSA при защите электронных платежей с применением кредитных карточек естественным является требование использования небольших значений экспоненты 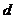у владельца карточки и большого значения экспоненты e у центрального компьютера.

Однако выбор малых параметров и 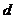представляется небезо­пасным по ряду соображений. Если малым является секретный параметр 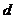, то можно применить метод перебора малых значений до получения искомого числа 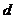. А если малым является параметр , то достаточно большое число от­крытых сообщений, удовлетворяющих неравенству будут зашиф­ровываться простым возведением в степень и поэтому их можно найти путем извлечения корня степени .

Другая аналогичная ситуация может сложиться, когда у нескольких абонентов используется одинаковая экспонента . Тогда становится возможна атака на основе Китайской теоремы об остатках (см. ниже).

Не нашли, что искали? Воспользуйтесь поиском: