Атака повторным шифрованием

Строим последовательность: . Итак, а так как , то существует такое натуральное число , что (следствие из расширенного алгоритма Эвклида). Но тогда (следствие из теоремы Эйлера), отсюда следует, что , значит, 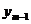– решение сравнения .

Пример 7. Пусть у нас имеется открытый ключ = 84517, = 397 и зашифрованное им сообщение = 8646. Необходимо найти исходный текст . Возведем в степень и получим = 37043. Будем повторять операцию до тех пор, пока не получим – искомое сообщение: =5569, =61833, 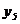= 83891, 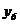= 16137, 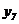= 8646. 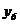является решением сравнения , а, следовательно, искомым сообщением .

Замечание. Анализ метода повторного шифрования хорошо показывает необходимость соблюдения требований на выбор и для обеспечения стойкости. В данном примере 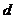= 82225. Неудачный выбор криптосистемы привел к тому, что атака методом повторного шифрования дала результат почти сразу, тогда как нахождение 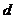потребовало бы на порядок больших вычислений.

Реализация атаки на алгоритм шифрования RSA методом повторного шифрования c помощью программы PS

Исходные данные: = 453819149023; = 1011817; = 442511634532.

1. Определить порядок экспоненты. Для этого необходимо ввести значение модуля в поле N, экспоненты в поле e, в поле Y записывается произвольное число, меньше чем N. После этого нужно нажать кнопку Запуск повторного шифрования и дождаться, пока в поле X появится значение, равное корню е степени от числа Y по модулю N, а в поле i – порядок e в конечном поле . В данном примере он составляет 435.

2. Дешифровать зашифрованный текст. Для этого нужно в область редактирования поля C поместить блоки зашифрованного текста, разделенные символом конца строки, значение модуля в поле N, экспоненты в поле e и порядка экспоненты в поле i. Затем нажать на кнопку Дешифрация и дождаться появления исходного текста в области редактирования M. Ответ – открытый текст – «null».

Не нашли, что искали? Воспользуйтесь поиском: