
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Атака на основе Китайской теоремы об остатках
Как отмечалось ранее, системы шифрования с открытыми ключами работают сравнительно медленно. Для повышения скорости шифрования RSA на практике используют малую экспоненту зашифрования.
Если выбрать число  небольшим или таким, чтобы в его двоичной записи было мало единиц, то процедуру шифрования можно значительно ускорить. Например, выбрав
небольшим или таким, чтобы в его двоичной записи было мало единиц, то процедуру шифрования можно значительно ускорить. Например, выбрав  = 3 (при этом ни
= 3 (при этом ни 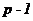 , ни
, ни  не должны делиться на 3), мы сможем реализовать шифрование с помощью одного возведения в квадрат по модулю
не должны делиться на 3), мы сможем реализовать шифрование с помощью одного возведения в квадрат по модулю  и одного перемножения. Выбрав
и одного перемножения. Выбрав 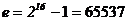 – число, двоичная запись которого содержит только две единицы, мы сможем реализовать шифрование с помощью 16 возведений в квадрат по модулю
– число, двоичная запись которого содержит только две единицы, мы сможем реализовать шифрование с помощью 16 возведений в квадрат по модулю  и одного перемножения. Если экспонента
и одного перемножения. Если экспонента  выбирается случайно, то реализация шифрования по алгоритму RSA потребует
выбирается случайно, то реализация шифрования по алгоритму RSA потребует 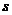 возведений в квадрат по модулю
возведений в квадрат по модулю  и в среднем
и в среднем  умножений по тому же модулю, где
умножений по тому же модулю, где 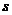 – длина двоичной записи числа
– длина двоичной записи числа  . Вместе с тем выбор небольшой экспоненты
. Вместе с тем выбор небольшой экспоненты  может привести к негативным последствиям. Дело в том, что у нескольких корреспондентов могут оказаться одинаковые экспоненты
может привести к негативным последствиям. Дело в том, что у нескольких корреспондентов могут оказаться одинаковые экспоненты  .
.
Пусть, например, три корреспондента имеют попарно взаимно простые модули  ,
,  ,
,  и общую экспоненту
и общую экспоненту  = 3. Если еще один пользователь посылает им некое циркулярное сообщение
= 3. Если еще один пользователь посылает им некое циркулярное сообщение  , то криптоаналитик противника может получить в свое распоряжение три шифрованных текста
, то криптоаналитик противника может получить в свое распоряжение три шифрованных текста 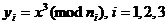 . Далее он может найти решение системы сравнений, лежащее в интервале
. Далее он может найти решение системы сравнений, лежащее в интервале  .
.

По китайской теореме об остатках такое решение единственно, а так как  , то
, то  . Значение
. Значение  можно найти, вычислив кубический корень
можно найти, вычислив кубический корень  .
.
Пример. Три пользователя имеют модули  =26549,
=26549,  =45901,
=45901,
 =25351. Все пользователи используют экспоненту
=25351. Все пользователи используют экспоненту  =3. Всем пользователям было послано некое сообщение
=3. Всем пользователям было послано некое сообщение  , причем пользователи получили сообщения
, причем пользователи получили сообщения  . Найдем
. Найдем  . Далее находим
. Далее находим


 = 84501028038745578 + 15301661957638980 + 121332116653000684 = 221134806649385242
= 84501028038745578 + 15301661957638980 + 121332116653000684 = 221134806649385242
 = 1000000000
= 1000000000
 = 1000 – исходное сообщение, отправленное пользователям.
= 1000 – исходное сообщение, отправленное пользователям.
Атака на алгоритм шифрования RSA, основанная на китайской теореме об остатках, c помощью программы «BCalc»
Исходные данные: n 1 = 363542076673; n 2 = 728740902979;
n 3 = 522993716719; y 1 = 246562834516; y 2 = 291375746601; y 3 = 222724269731.
Последовательно вычисляем следующие значения:

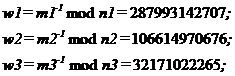
 =
=
=34867892796403337952181607384067689087012354329;
 = 67675640795094503562173784000;
= 67675640795094503562173784000;
M = (S mod M 0)^(1/ e) = 4075154940;
text(M) = «тень».
Ниже приведен снимок экрана с окном программы «BCalc».
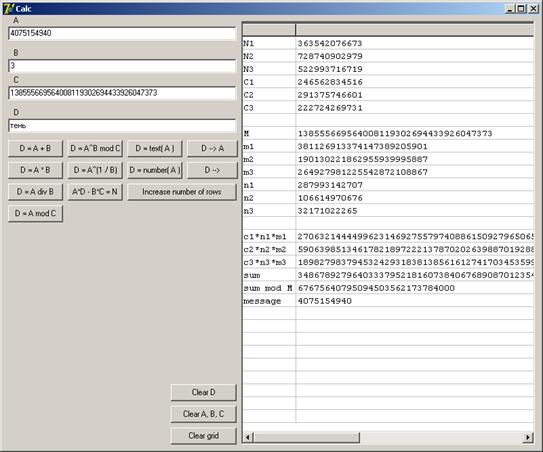
Бесключевое чтение
Пусть два пользователя выбрали одинаковый модуль  и разные экспоненты
и разные экспоненты 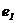 и
и  . Если один пользователь посылает им некое циркулярное сообщение
. Если один пользователь посылает им некое циркулярное сообщение  то криптоаналитик противника может получить в свое распоряжение два шифрованных текста
то криптоаналитик противника может получить в свое распоряжение два шифрованных текста  и
и  В таком случае криптоаналитик может получить исходное сообщение, используя расширенный алгоритм Евклида, находим
В таком случае криптоаналитик может получить исходное сообщение, используя расширенный алгоритм Евклида, находим  такие, что
такие, что  . Отсюда получаем:
. Отсюда получаем: 
Пример. Два пользователя применяют общий модуль  = 137759, но разные взаимно простые экспоненты
= 137759, но разные взаимно простые экспоненты 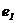 = 191 и
= 191 и  = 233. Пользователи получили шифртексты
= 233. Пользователи получили шифртексты  = 60197 и
= 60197 и  = 63656, которые содержат одно и то же сообщение. Найдем исходное сообщение методом бесключевого чтения. Так как
= 63656, которые содержат одно и то же сообщение. Найдем исходное сообщение методом бесключевого чтения. Так как 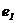 и
и  взаимно просты, то найдем такие
взаимно просты, то найдем такие  , что
, что  . С помощью расширенного алгоритма Евклида находим
. С помощью расширенного алгоритма Евклида находим  . Искомое сообщение
. Искомое сообщение 
Атака на алгоритм шифрования RSA методом бесключевого чтения c помощью программы «bcalc»
Исходные данные: n = 357114156277; e 1 = 1025537; e 2 = 722983;
C 1 = 68639736967; C 2 = 204258645263.
1. Решаем уравнение e 1∙ r – e 2∙ s = ±1. Для этого в поле A помещаем значение e 1, в поле B – значение e 2. Нажимаем кнопку «A∙D – B∙C = N», затем – кнопку C = s = 406030; D = r = 286243.
2. Производим дешифрацию: c 1 возводим в степень r, а c 2 – в степень – s по модулю N, тогда c 1^ r = 189703239311, c 2^(– s) = 104340380259.
После этого результаты перемножаем и получаем, что m ^(e 1∙ r – e 2∙ s) =
= 19793708126073817161549. Далее берем модуль от полученного значения: (m ^(e 1∙ r – e 2∙ s) mod N) = 1381187873 и преобразуем в текст «RSA!».
Ниже приведен снимок экрана с окном программы «BCalc».
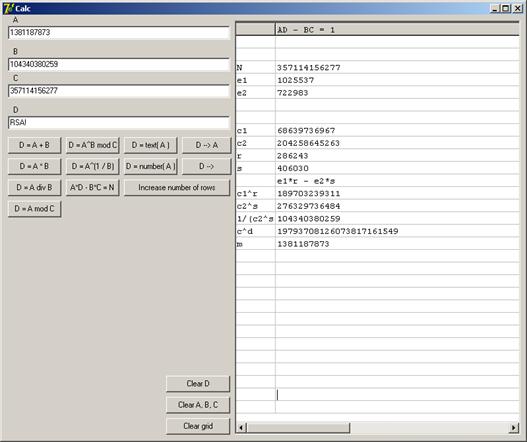
Как видно из приведенных выше примеров (а также из примеров выполнения заданий лабораторных работ) выбор параметров криптосистемы является ответственной задачей. Параметры необходимо выбирать в строгом соответствии с требованиями. Существующими в настоящими время методами (и при использовании существующих в настоящее время вычислительных мощностей) атака на алгоритм и/или криптосистему возможна лишь при неудачном выборе параметров. В процессе выполнения заданий лабораторной работы вы убедитесь в обоснованности перечисленных требований к параметрам криптосистемы. В частности, необходимо обеспечить каждому пользователю уникальные значения  ,
,  и уникальное значение
и уникальное значение  , удовлетворяющие требованиям, приведенным выше.
, удовлетворяющие требованиям, приведенным выше.
Описание программы «BCalc»
Программа «BCalc» предназначена для работы с целыми числами большой размерности и включает в себя возможность выполнения базовых и некоторых специальных операций над целыми числами. К специальным относятся следующие операции:
– преобразование числа в данные и обратно;
– возведение в степень по модулю;
– вычисление обратных значений по модулю;
– нахождение целых корней любых натуральных степеней;
– нахождение подходящих дробей для цепной дроби.
Описание интерфейса программы
В окне программы находятся следующие элементы интерфейса:
– поля ввода, помеченные латинскими буквами A, B, C, D;
– верхняя группа кнопок с обозначением выполняемых действий на них;
– нижняя группа кнопок, предназначенных для очистки полей и таблицы;
– таблица для хранения промежуточных результатов.
Поля ввода A, B, C хранят входные данные для вызываемых функций программы. Результаты работы этих функций помещаются в поле D. При нахождении подходящей дроби результат помещается в поле C и первую строку таблицы.
Для любого поля таблицы можно вызвать контекстное меню указателем мыши, нажав ее правую кнопку, в котором содержатся следующие пункты:
– «To [поле ввода]» – копирует значение ячейки таблицы в соответствующее поле ввода;
– «From [поле ввода]» – копирует значение соответствующего поля ввода в выбранную ячейку таблицы.
Кнопки «Clear D», «Clear A, B, C», «Clear grid» очищают соответственно поле D, поля A, B, C – таблицу.
Кнопка «Increase number of rows» увеличивает количество строк в таблице на пять.
Кнопка «D –> A» копирует значение, находящееся в данный момент в поле D, в поле A. Кнопка «D –>» копирует значение поля D в первую сверху пустую ячейку второй колонки таблицы.
Остальные кнопки запускают математические функции, описанные ниже.
Математические функции программы
«D = A + B» – значения A и B складываются, результат помещается
в поле D.
«D = A ∙ B» – значения A и B перемножаются, результат помещается
в поле D.
«D = A div B» – в D помещается результат целочисленного деления A на B.
«D = A mod B» – в D помещается остаток от целочисленного деления
A на B.
«D = A ^ B mod C» – в D помещается результат возведения A в степень B по модулю C. Экспонента может быть отрицательным числом. Если поле C = 0, то возведение в степень будет происходить не по правилам модульной арифметики. В таком случае не стоит задавать в качестве экспоненты большие числа, так как вычисления могут занять слишком много времени. Невозможно также вычислять обратные значения, если в качестве модуля задан ноль.
«D = A ^(1/ B)» – в поле D помещается корень B степени от A. Если в результате извлечения корня получилось нецелое число, то в D помещается ближайшее бόльшее целое число, а в первой строке таблицы появится надпись «[error]».
«A ∙ D – B ∙ C = N», где – A – числитель дроби; B – знаменатель подходящей дроби d n порядка. В поле C будет помещен числитель, а в D – знаменатель подходящей дроби d n -1 порядка. В первую строку таблицы будет помещено значение выражения A ∙ D – B ∙ C. Если после начала вычисления дроби поля C и D равны нулю, то это значит, что числа A и B не взаимно просты.
«D = text(A)» – число A интерпретируется как строка из символов в ANSI- кодировке. Строка помещается в поле D.
«D = number(A)» – строка A, состоящая из символов, интерпретируется как число и помещается в поле редактирования D.
В программе используется модернизированный модуль «BigNum v2.0»
(Jes R. Klinke).
Описание программы «PS»
Программа PS предназначена для нахождения порядка чисел в конечном поле  и дешифрации сообщений методом перешифрования.
и дешифрации сообщений методом перешифрования.
Нахождение порядка чисел
Для нахождения порядка числа методом перешифрования следует указать в поле редактирования N значение модуля, в поле e – экспоненты, а в поле Y – произвольное число, меньшее чем модуль. При нажатии кнопки Запуск повторного шифрования программа начнет возводить число Y в степень e (т. е.  ) до тех пор, пока Yi не будет равен Y. Значение
) до тех пор, пока Yi не будет равен Y. Значение  , а число шагов повторного шифрования является порядком числа
, а число шагов повторного шифрования является порядком числа  в конечном поле
в конечном поле  . При завершении работы алгоритма в поле
. При завершении работы алгоритма в поле  будет записано количество шагов повторного шифрования, а в поле
будет записано количество шагов повторного шифрования, а в поле 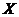 – значение
– значение  . Во время работы программы кнопка Pause приостанавливает работу алгоритма. Для продолжения работы следует нажать кнопку Pause еще раз. Флаг «Show results» указывает, будут ли отображаться результаты промежуточных вычислений. Его отключение увеличивает скорость работы приблизительно на 20 %.
. Во время работы программы кнопка Pause приостанавливает работу алгоритма. Для продолжения работы следует нажать кнопку Pause еще раз. Флаг «Show results» указывает, будут ли отображаться результаты промежуточных вычислений. Его отключение увеличивает скорость работы приблизительно на 20 %.
Дешифрация сообщений методом перешифрования
Для дешифрации сообщения необходимо указать в поле редактирования N значение модуля, в поле  – экспоненты, в поле
– экспоненты, в поле  – порядок экспоненты, а в область редактирования C поместить блоки зашифрованного текста (разделитель – символ конца строки). При нажатии кнопки Дешифрация начнется процесс вычисления исходного сообщения. Результат будет помещен в область редактирования
– порядок экспоненты, а в область редактирования C поместить блоки зашифрованного текста (разделитель – символ конца строки). При нажатии кнопки Дешифрация начнется процесс вычисления исходного сообщения. Результат будет помещен в область редактирования  .
.
В программе используется модернизированный модуль «BigNum v2.0» автор (Jes R. Klinke).
Варианты заданий для лабораторных работ
Таблица 1
Варианты исходных данных к заданию 2
| Вариант | Модуль, N | Экспонента, е | Блок зашифрованного текста, C |
Таблица 2
Варианты исходных данных к заданию 3
| Вариант | Модуль, N | Экспонента, e | Блок зашифрованного текста, С |
Таблица 3
Варианты исходных данных к заданию 4
| Вариант | Модуль, N | Экспоненты | Блок зашифрованного текста | ||
| e 1 | e 2 | C 1 | C2 | ||
Таблица 4
Варианты исходных данных к заданию 2
| Вариант | Модуль | Блок зашифрованного текста | ||||
| N 1 | N 2 | N 3 | C 1 | C 2 | C 3 | |
Не нашли, что искали? Воспользуйтесь поиском: