Атаки на алгоритм RSA

Взлом RSA при неудачном выборе параметров криптосистемы (Метод Ферма)

Само по себе использование RSA не обеспечивает безопасности. Дело еще в деталях реализации. Приведем ряд примеров. Для простоты вычислений будем работать с небольшими числами. Цель – показать особенности, не зависящие от размера.

Пример. Пусть пользователь выбрал = 2047, = 179, 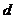= 411. Так как 2047 = 23×89, а 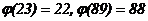имеют наименьшее общее кратное 88, то любой обратный к 179 по модулю 88, например 59, будет действовать как .

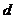Пример. Число = 536813567 является произведением простого числа Мерсенна 8191 и простого числа Ферма 65537. Это очень плохой выбор.

Пример. Число 23360947609 является очень плохим выбором для из-за того, что два его простых делителя слишком близки к друг другу. Пусть , тогда имеем 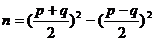. Обозначим: . Так как 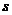мало, то – целое число, лишь немного большее причем является полным квадратом. Проверяем подряд целые числа 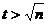. В нашем примере = 152843, = 152844, = 152845 и , тогда , . Таким образом, мы с третьей попытки нашли и . Количество попыток, необходимых для факторизации , можно при известных и вычислить по следующей формуле: , где – операция округления до ближайшего целого числа.

Релизация атаки на алгоритм шифрования RSA посредством метода Ферма c помощью программы BCalc

Исходные данные: N = 65815671868057; e = 7423489; C = 38932868535359. Найти

1. Вычисляем n = [sqrt(N)] + 1. В поле A помещаем N, в поле B – 2; нажимаем кнопку «D = A ^(1/ B)». В поле D заносится число 8112686, в первую строку таблицы – сообщение «[error]». Это свидетельствует, о том, что N не является квадратом целого числа.

2. t ₁ = n + 1. Возводим число t ₁ в квадрат: A: = 8112687, B: = 2, C: = 0 (возведение в квадрат будет производиться не по правилам модульной арифметики), нажимаем «D = A ^ B mod C» => D = t ₁^2 = 65815690359969.

Вычисляем w ₁ = t ₁^2 – N. Для этого A:= t ₁^2, B:= – N, затем нажимаем «D = A + B» => D= w ₁ = 18491912. Проверяем, является ли w ₁ квадратом целого числа: A:= w ₁,
B:= 2, нажимаем «D = A ^(1/ B)» => в первой строке таблицы появляется сообщение «[error]», следовательно проделываем п. 2 заново с t ₂ = n + 2 и так далее, пока не найдем, что некое w _i является квадратом целого числа.

3. При вычислении квадратного корня w ₅ первая строка таблицы остается пустой, а D = sqrt(w ₅) = 9132, что свидетельствует об успехе факторизации. t ₅ = 8112691.

4. Вычисляем p = t ₅ + sqrt(w ₅); A:= t ₅, B:= sqrt(w ₅), нажимаем «D = A + B» => D = p = 8121823; q = t ₅ – sqrt(w ₅) = 8103559.

Вычисляем Phi(N) = (p – 1)(q – 1), A:= 8121822, B:= 8103558, нажимаем «D = A ∙ B» => D= Phi(N) = 65815655642676.

Вычисляем d, как обратный к e: A:= e, B:= –1, C:= Phi(N), нажимаем «D = A ^ B mod C» => D = d = 12490789985101.

5. Производим дешифрацию шифрблока С: A:= C; B:= d; C:= N. Нажимаем «D = A ^ B mod C». В поле D находится исходное сообщение M = 3402418120. Переводим M в текстовый вид. Для этого A:= M, нажимаем «D = text(A)» => D = = «КМЗИ».

Снимок экрана с окном программы «BCalc» приведен ниже.

Не нашли, что искали? Воспользуйтесь поиском: