Механизм намагничивания веществ

В вакууме источником магнитного поля являются движущиеся заряды или токи в проводниках. В поле вещество способно намагничиваться, то есть приобретать магнитный момент, в результате чего создается поле . Поэтому результирующее поле в веществе:

Основные виды магнетиков:

Диамагнетики – несколько ослабляют внешнее магнитное поле (хотя идеальные диамагнетики полностью вытесняют магнитное поле из вещества – эффект Мейсснера в сверхпроводниках).

Парамагнетики – слабо усиливают внешнее магнитное поле.

Ферромагнетики – усиливают магнитное поле в тысячи раз благодаря доменной структуре (в веществе можно выделить области спонтанного намагничивания (домены) размером , каждая из которых намагничивается до насыщения). Ферромагнитные свойства проявляются только до определённой температуры (точка Кюри , , ). При циклическом намагничивании–размагничивании зависимость магнитной индукции поля от внешнего поля образует петлю гистерезиса.

Антиферромагнетики – магнитные моменты атомов тоже упорядочены, но противоположно для каждой пары соседних атомов и взаимно компенсируют друг друга. Свойства как у очень слабых парамагнетиков.

Ферримагнетики – противоположно ориентированные подрешетки имеют разные по величине магнитные моменты и они не компенсируют друг друга. Свойства отличаются от ферромагнетиков только другой зависимостью намагничивания от температуры и низкой точкой Кюри.

Полевые теоремы магнитного поля в веществе:

– интегральная форма теоремы о циркуляции вектора намагниченности .

Намагниченность – магнитный момент единицы объема вещества: .

– ток намагничивания (нескомпенсированный макроскопический ток на поверхности вещества, возникающий вследствие выхода на поверхность молекулярных токов).

– дифференциальная форма теоремы о циркуляции .

– плотность молекулярного тока намагничивания

– интегральная форма теоремы о циркуляции

– дифференциальная форма теоремы о циркуляции .

Напряженность магнитного поля .

Для изотропных неферромагнитных магнетиков, в слабых полях: ,

– магнитная восприимчивость вещества (безразмерная величина).

, откуда для изотропных неферромагнетиков: ,

– магнитная проницаемость вещества (безразмерная величина).

В вакууме , в веществе:

• в диамагнетиках
• в парамагнетиках
• в ферромагнетиках

При решении задач на расчет вектора используется теорема о циркуляции вектора , так как она определяется только токами проводимости, а затем находят .

Условия для и на границе раздела двух магнетиков (следствие т. Гаусса для и т. о циркуляции ):

Преломление линий векторов и на границе раздела: ;

.

Чем , тем > касательная составляющая (линии сгущаются в веществе с , например – в железной оболочке при осуществлении магнитной защиты).

– в среде с некоторые линии обрываются, так как в ней возникает большая плотность молекулярных токов. Некомпенсированные молекулярные токи являются источниками дополнительных линий .

Магнито-механические явления: намагничивание магнетика приводит к его вращению (опыт Эйнштейна и де Гааза), а вращение магнетика вызывает его намагничивание (опыт Барнетта).

Электромагнитная индукция

В неподвижном контуре со скользящей перемычкой длиной во внешнем однородном магнитном поле индукцией плоскости контура, при перемещении перемычки на под действием силы Ампера, эта сила совершает работу:

Закон электромагнитной индукции (закон Фарадея).

Электрические и магнитные поля связаны друг с другом. Кроме того, разделение электромагнитного поля на электрическую и магнитную составляющие относительно (связано с выбором системы отсчёта).

Явление электромагнитной индукции (1831г., М. Фарадей): в замкнутом проводящем контуре при изменении потока магнитной индукции, возникает электрический ток (индукционный ток): (изменяющееся магнитное поле порождает электрическое поле (вихревое, соленоидальное)).

Правило Ленца: индукционный ток направлен так, что созданное им поле препятствует изменению магнитного потока.

Раз возникает ток, значит при изменении магнитного потока, пронизывающего контур, возникает ЭДС – электродвижущая сила индукции , которая определяется не способом изменения магнитного потока через контур, а лишь скоростью его изменения: . Способы изменения потока через контур:

1. Взаимное перемещение контура (его части) и источника магнитного поля .

2. Изменение поля , созданного источником (переменное магнитное поле).

Максвелл предположил, что независимо от наличия проводника изменяющееся во времени магнитное поле вызывает возникновение вихревого электрического поля (одно из 4 уравнений Максвелла для неподвижных сред): – основной закон электромагнитной индукции (интегральная форма);

(дифференциальная форма).

В массивных проводниках индукционный ток называют током Фуко – используют для демпфирования (торможения) подвижных частей приборов, в индукционных печах – для нагрева. Но нагрев чаще нежелателен – потери энергии (в трансформаторах сердечник набирают из изолированных пластинок). Токи Фуко вытесняют переменные токи проводимости на поверхность проводника (скин-эффект не проявляется при промышленной частоте 50 Гц).

.

Самоиндукция – явление возникновение ЭДС индукции в контуре при изменении тока в этом же контуре . По принципу Ленца ЭДС самоиндукции стремится воспрепятствовать изменению силы тока в контуре, (явление самоиндукции приводит к инерционности тока).

Если в проводнике, где находится контур с током, нет ферромагнетиков, B ~ I, значит : ,

L – индуктивность (зависит от формы и размеров контура и от свойств окружающей среды).

L не зависит от I, если контур жесткий (форма не меняется) и в окружающей среде нет ферромагнетика.

.

Например, индуктивность соленоида с n витков на ед. длины, заполненного веществом с магнитной проницаемостью : через 1 виток:

Потокосцепление (полный магнитный поток через N витков): .

(индуктивность контура ~ квадрату плотности витков).

ЭДС самоиндукции: (если );

Если же , то .

Примеры проявления явления самоиндукции:

1. Убывание тока при размыкании цепи с индуктивностью: , – время релаксации, .

2. Нарастание тока при замыкании цепи с индуктивностью: .

Взаимная индукция

В 1 контуре течет ток , создавший во 2-м контуре поток : .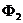

Если ток течет во втором контуре , то он создает в первом контуре поток: .

и – взаимные индуктивности контуров (зависят от формы, размеров, взаимного расположения контуров и от свойств окружающей среды).

Теорема взаимности: (если ток I в первом контуре вызывает во втором контуре поток , то такой же ток I, протекающий во втором контуре вызывает тоже поток в первом контуре, независимо от их размеров).

Магнитная связь между контурами: при изменении тока в первом контуре возникает ЭДС индукции во втором контуре – взаимная индукция.

.

С учетом самоиндукции и взаимной индукции закон Ома: .

Энергия магнитного поля: .

Энергия электромагнитного поля: .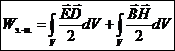

Ток смещения

Линии тока смещения замыкают в контуре с конденсатором линии переменного тока проводимости.

Максвелл (1865г.): плотность полного тока): .

Уравнение непрерывности в дифференциальной форме:

Ток смещения – условное название. Он, также как и ток проводимости создает магнитное поле, может проявляться везде, где есть переменное электрическое поле.

, .

Уравнения Максвелла в неподвижных средах

Уравнения Максвелла в интегральной форме:

а) в переменных полях:

1) (закон электромагнитной индукции – переменное во времени магнитное поле вызывает возникновение вихревого (соленоидального) электрического поля);

2) (в природе не существует магнитных зарядов);

3) (основано на теореме о непрерывности; источниками магнитного поля могут быть как токи проводимости, так и токи смещения);

4) (электрические заряды являются источником электрического поля).

Чтобы получить дифференциальную форму уравнений применяют:

· к (1) и (3) – теорему Стокса ;

· к (2) и (4) – теорему Остроградского–Гаусса .

Уравнения Максвелла в дифференциальной форме:

1) теорема о циркуляции: ;

2) теорема Гаусса: ;

3) теорема о циркуляции: ;

4) теорема Гаусса: .

Электрическое поле может создаваться электрическими зарядами и переменными магнитными полями.

Магнитное поле может возбуждаться движущимися электрическими зарядами и переменными электрическими полями.

б) Для стационарных полей уравнения для электрических и магнитных полей независимы:

1) ;

2) ;

3) ;

4) .

Уравнения Максвелла в дифференциальной форме предполагают непрерывность в изменении всех величин. Для общности их дополняют граничными условиями: .

Систему уравнений Максвелла дополняют материальными уравнениями, характеризующими свойства среды, в которой возбуждается электромагнитное поле: (слабые, медленно меняющиеся в пространстве и во времени поля; изотропные, не содержащие сегнетоэлектриков и ферромагнетиков среды).

Уравнения Максвелла релятивистски инвариантны

Из уравнений Максвелла можно получить волновые уравнения: и .

Электромагнитные волны

Из уравнений Максвелла следует возможность существования электромагнитных волн, то есть электромагнитных полей, распространяющихся в среде с фазовой скоростью .

Свойства плоских (т.е., имеющих плоский волновой фронт) электромагнитных волн:

1.

2. Связь между мгновенными значениями и : (колебания и в плоской электромагнитной волне синфазны).

3. Плотность энергии электромагнитного поля: ;

Поток энергии – количество энергии, переносимое волной через некоторую поверхность в единицу времени: (имеет размерность мощности).

Плотность потока энергии – поток энергии через единичную, перпендикулярную направлению переноса энергии, площадку. Для электромагнитной волны – вектор Пойнтинга:

Интенсивность – модуль среднего по времени значения плотности потока энергии, переносимой световой волной: .

Электромагнитные колебания (см. также механические колебания)

Закон Ома для замкнутой RLC–цепи, не содержащей внешнего источника тока (свободные () и затухающие () колебания): ,

где – напряжение на конденсаторе, – заряд конденсатора, – ток в цепи, – ЭДС самоиндукции катушки.

Иначе его можно записать: , где , – коэффициент затухания, – собственная частота колебаний контура. Частота затухающих колебаний: . При колебаний не будет (апериодический процесс).

При решение уравнения затухающих колебаний: , через напряжение на конденсаторе: , а через силу тока в цепи: , где , (сила тока опережает напряжение на конденсаторе при на , а при на ). При слабом затухании логарифмический декремент затухания: , а добротность: .

Закон Ома для замкнутой RLC–цепи, содержащей внешний источник тока (вынужденные колебания): или .

Решение этого уравнения для установившихся колебаний: , где , а ,

а через силу тока в цепи: , где – сдвиг фазы между током и приложенным напряжением, .

Напряжение на: – активном сопротивлении (совпадает по фазе с током);

– конденсаторе ;

– индуктивности .

Резонансная частота для заряда и напряжения: ; резонансная частота для тока: .

Переменный ток

, ; ;

– полное электрическое сопротивление (импеданс);

– реактивное индуктивное сопротивление;

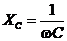– реактивное ёмкостное сопротивление;

– реактивное сопротивление.

Среднее по времени значение мощности: .

Такую же мощность имеет постоянный ток – действующее значение силы тока.

– действующее значение напряжения.

Среднее по времени значение мощности можно записать через действующие значения силы тока и напряжения: .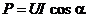

Аналогия между электромагнитными и механическими (например, упругими) колебаниями:

Электромагнитные колебания	Механические колебания
заряд конденсатора	координата
сила тока	скорость
индуктивность	масса
(ёмкость)-1	коэффициент упругости
напряжение на конденсаторе	сила упругости
электрическая энергия на конденсаторе	потенциальная энергия пружины
магнитная энергия катушки	кинетическая энергия груза
магнитный поток	импульс

Не нашли, что искали? Воспользуйтесь поиском: