Источник тока. Электродвижущая сила и напряжение

Для того, чтобы в проводнике мог существовать постоянный ток проводимости, необходимо выполнение следующих условий:

а) цепь постоянного тока проводимости должны быть замкнутой.

б) напряженность электрического поля в проводнике должна быть отлична от нуля и не должна изменяться со временем; то есть на свободные электрические заряды должны действовать силы, обеспечивающие их упорядоченное перемещение в течение конечного промежутка времени. Для этой цели в электрической цепи постоянного тока необходимо иметь специальное устройство, внутри которого происходило бы непрерывное разделение разноименных зарядов и перенос их к соответствующим проводникам – клеммам. Подобное устройство, называемое источником тока, должно действовать на электрические заряды силами неэлектростатического происхождения. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах (батареях) эти силы возникают за счет энергии химических реакций между электронами и электролитами; в генераторах постоянного тока – за счет энергии магнитного поля и механической энергии вращения якоря (разделение электрических зарядов происходит в результате действия на них силы Лоренца) и т.д. За счет создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах внешней цепи (цепи потребителя) поддерживается разность потенциалов и в цепи течет постоянный электрический ток.

Сторонние силы, перемещая заряды, совершают работу, поэтому электрические батареи в процессе эксплуатации истощаются. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (эдс) E, действующей в цепи:

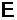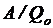= (2.1)

Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину E можно также называть электродвижущей силой источника тока, включенного в цепь. Эдс, как и потенциал, измеряется в вольтах (1 В = 1 Дж / 1 Кл).

Сторонняя сила F _стор, действующая на заряд 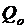может быть выражена как

F _стор = Е _стор 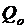, (2.2)

где Е _стор - напряженность поля сторонних сил. Работа же сторонних сил над зарядом 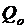на замкнутом участке цепи равна

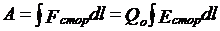(2.3)

Разделив (2.3) на 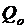, получим эдс, действующую в цепи.

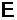
, (2.4)

т.е. эдс, действующая в цепи определяется как циркуляция вектора напряженности сторонних сил. Эдс, действующая на участке цепи 1-2, равна

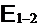
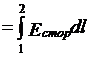. (2.5)

На заряд 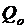помимо сторонних сил действуют также силы электростатического поля 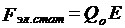. Таким образом, результирующая сила, действующая в цепи на заряд, равна

.

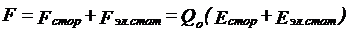Работа, совершаемая результирующей силой над зарядом 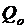на участке цепи 1-2, равна

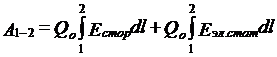. (2.6)

Используя формулы (2.4) и , можем записать

(2.7)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в данном случае .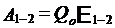

Напряжением U на участке 1-2 называется физическая величина, определяемая работой, совершаемой суммарным действием электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Таким образом, согласно (2.7),

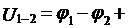
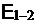. (2.8)

Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не приложена электродвижущая сила (т.е. нет источника тока и поэтому сторонние силы отсутствуют).

3. Закон Ома.

Немецкий физик Г.Ом (1787-1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

I = U / R, (3.1)

где R - электрическое сопротивление проводника. Уравнение (3.1) выражает закон Ома для участка цепи (не содержащего источника тока): сила тока I в проводнике прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника R. Формула (3.1) позволяет установить единицу сопротивления – Ом: 1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток силой 1 А. Для измерения больших сопротивлений употребляют более крупные единицы: 1 килоом (Ком)= 10³ Ом и 1 мегаом (Мом) = 10⁶ Ом.

Величина G = 1 / R называется электрической проводимостью. Единица проводимости - Сименс (См): 1 См – проводимость участка электрической цепи сопротивлением 1 Ом.

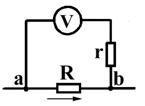
На использовании закона Ома основано измерение напряжений при помощи вольтметра. Вольтметр представляет собой гальванометр, последовательно с которым соединено большое сопротивление r. При подключении вольтметра к каким – либо точкам a и b участка цепи в вольтметр ответвляется часть тока; сила ответвленного тока i по закону Ома пропорциональна напряжению U между этими точками: i = U / R.

Поэтому, зная чувствительность вольтметра по току и его сопротивление r, можно определить и напряжение U. Это напряжение наносят непосредственно на шкалу прибора. Чтобы подключение вольтметра существенно не изменило силу тока и распределение напряжение в цепи, ток вольтметра должен быть мал по сравнению с током цепи, а для этого сопротивление вольтметра r должно быть велико по сравнению с сопротивлением R участка цепи ab.

Сопротивление (и электропроводимость) проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для цилиндрического проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

R = r l / S, (3.2)

где r - коэффициент пропорциональности, характеризующий материал проводника, называемым удельным электрическим сопротивлением. Единица удельного электрического сопротивления - ом^.метр (Ом^.м)

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (3.2) в закон Ома (3.1), получим

I / S = U / r l = g U / l (3.3)

где величина g = 1/ r, обратная удельному сопротивлению называется удельной электрической проводимостью вещества проводника. Ее единица измерения – сименс деленный на метр (См/м). Учитывая, что U / l = E - напряженность электрического поля в проводнике, I / S = j - плотность тока, формулу (3.3) можно записать в виде

j = g E. (3.4)

Так как носители заряда в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому формулу (3.4) можно записать в виде

j = g E. (3.4)

Выражение (3.4) – закон Ома в дифференциальной (векторной) форме, связывающий плотность тока в любой точке с напряженностью электрического поля в этой же точке. В отличие от (3.1) – интегральной формы закона Ома – оно содержит величины, характеризующие электрическое состояние среды в одной и той же точке. Соотношение (3.4) справедливо и для переменных полей.

Удельное сопротивление r зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:

a = dr / rdT, (3.5)

Температурный коэффициент сопротивления характеризует относительное приращение сопротивления при увеличении температуры на один градус.

Температурный коэффициент сопротивления a для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от нее более сложным образом. Однако для многих проводников, к которым относятся все металлы, изменение a с температурой не очень велико. Если еще интервал изменения температуры достаточно мал, то приближенно можно считать a постоянным, равным его среднему значению внутри рассматриваемой области температур. Так, например, если r_о есть удельное сопротивление при 0^оС, а r_t – его значение при t ^оС, то можно положить

r_t = r_o (1 + a t) (3.6)

или

R _t = R _o (1+ a t). (3.7)

Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов (проводники первого класса) сопротивление увеличивается с увеличением температуры, и следовательно для металлов a > 0. У всех электролитов (проводники второго класса) в отличие от металлов сопротивление при нагревании всегда уменьшается. Для всех чистых металлов температурный коэффициент сопротивления близок к 1/273 град ^-1, т.е. к величине температурного коэффициента расширения газов. Значит зависимость сопротивления R (t) (3.6) может быть представлена в виде

R _T = a R _o T, (3.8)

где Т – термодинамическая температура (в шкале Кельвина).

На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления, которые позволяют по градуированной взаимосвязи сопротивления от температуры измерять температуру с точностью до 10^-3К. Использование же в качестве рабочего вещества термометра сопротивления полупроводников, приготовленных по специальной технологии, - термисторов, - позволяет отмечать изменение температуры в миллионные доли кельвина и использовать термисторы для измерения температур очень малых объемов (ввиду малых габаритов полупроводниковых приборов).

Согласно (3.7), удельное сопротивление металлов должно уменьшаться при охлаждении, оставаясь при всех температурах конечным. Такая линейная зависимость сопротивления действительно наблюдается на опыте при сравнительно высоких температурах. Однако, в области низких температур удельное сопротивление перестает зависеть от температуры и достигает некоторого предельного значения. Оно различно для разных веществ и даже для разных образцов одного и того же вещества. Это остаточное удельное сопротивление тем меньше, чем чище металл и чем меньше структурных дефектов содержит исследуемый образец.

Если понижать температуру еще больше, то в некоторых веществах наблюдается сверхпроводимость – при некоторой критической температуре, (0,15 – 20 К) удельное сопротивление скачком уменьшается практически до нуля. Сверхпроводимость наблюдается не только у элементов, но и во многих химических соединениях и сплавах. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Примерами могут служить сплавы NiBi, Au₂Bi, PdTe, PtSb и другие.

Вещества в сверхпроводящем состоянии обладают исключительно необычными свойствами - в них однажды возбужденный электрический ток может длительно существовать без источника тока. Внутри вещества в сверхпроводящем состоянии нельзя создать магнитное поле, потому что при всяком изменении магнитного потока в сверхпроводниках возникают индукционные токи, которые в соответствии с законом Ленца компенсируют эти изменения. В обычном проводнике индукционные токи быстро затухают и остается лишь поток, обусловленный намагничивающими катушками. В случае же сверхпроводника индукционные токи не затухают и поэтому все время компенсируют изменения внешнего поля. Внешнее магнитное поле разрушает состояние сверхпроводимости. Чем сильнее охлажден образец ниже температуры перехода в сверхпроводящее состояние, тем больше и критическое магнитное поле, при котором исчезает сверхпроводимость. При температуре перехода в сверхпроводящее состояние критическое поле равно нулю.

В настоящее время интенсивно изучаются высокотемпературные сверхпроводники (керамика на основе окиси иттрия, легированная РЗЭ), для которых температура перехода в сверхпроводящее состояние составляет 100 – 150 К.

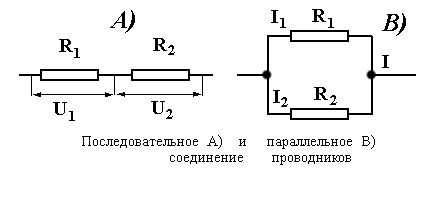
4. Последовательное и параллельное соединение проводников.

На практике электрические цепи никогда не состоят из однородных проводников постоянного сечения, а представляют собой совокупность различных проводников, определенным образом соединенных между собой. Как можно найти сопротивление сложной цепи, если известно сопротивление отдельных проводников, ее составляющих?

Рассмотрим случай двух проводников, включенных в цепь последовательно. Пусть сопротивления отдельных проводников равны R ₁ и R ₂. Сила тока I в обоих проводниках одинакова. Однако напряжения U ₁ и U ₂ между концами каждого из проводников различны. На основании закона Ома имеем U ₁= I R₁ и U ₂= I R₂, поэтому

U ₁ / U ₂ = R ₁ / R ₂ (4.1)

При последовательном соединении напряжение на каждом из проводников пропорционально его сопротивлению.

Полное сопротивление U между началом первого проводника и концом второго равна сумме этих напряжений. Поэтому U = U ₁ + U ₂ = I R ₁ + I R ₂ = I (R ₁ + R ₂). Если обозначить через R сопротивление всего участка цепи, состоящего из сопротивлений R ₁ и R ₂, то по закону Ома U = I R. Из сравнения двух последних формул следует, что R = R ₁ + R ₂. Проводя подобные рассуждения для трех, четырех и, вообще n проводников, получим, очевидно, следующий результат:

R = R ₁ + R ₂ + … + R_n . (4.2)

При последовательном соединении проводников их сопротивления складываются.

Рассмотрим параллельное соединение двух проводников с сопротивлениями R ₁и R ₂. Ток I, идущий по общей цепи, входя в группу проводников R ₁ и R ₂, разветвляется на два тока I ₁ и I ₂, при этом сумма токов в разветвленной частях цепи равна току в общей цепи:

I = I ₁ + I ₂. (4.3)

Соотношение сил токов I ₁ и I ₂ зависит от сопротивлений R ₁ и R ₂ Действительно, на основании закона Ома напряжение на концах первого проводника U ₁ = I ₁ R ₁, а на концах второго проводника U ₂ = I ₂ R ₂. Но обе эти величины равны друг другу, так как каждая из них есть напряжение между одними и теми же точками разветвленной цепи. Итак, U ₁ = U ₂, т.е.

I ₁ / I ₂ = R ₂ / R ₁. (4.4)

Не нашли, что искали? Воспользуйтесь поиском: