
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теорема Поста о полноте
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T 0, T 1, L, S, M.
Следствие. Всякий замкнутый класс функций из Р 2, не совпадающий с Р 2 содержится, по крайней мере, в одном из замкнутых классов T 0, T 1, L, S, M.
1. Покажем, что система функций { f 1 = x 1 x 2, f 2 =0, f 3 =1, f 4 = x 1Å x 2Å x 3} полна в Р 2. Составим таблицу, которая называется критериальной:
2.
| Т 0 | Т 1 | L | M | S | |
| x 1 x 2 | + | + | - | + | - |
| + | - | + | + | - | |
| - | + | + | + | - | |
| x 1Å x 2Å x 3 | + | + | + | - | + |
| x 1 x 2 x 3 | x 1Å x 2Å x 3 |
| 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Из таблицы видно, что какой бы класс мы ни взяли, всегда есть функция из данной системы, которая в этот класс не входит. Можно сформулировать следующее правило: для того чтобы система функций была полна, необходимо и достаточно, чтобы в каждом столбце критериальной таблицы был хотя бы один «минус».
Отметим еще одно обстоятельство, касающееся приведенной системы. Какую бы функцию из этой системы мы ни удалили, система станет неполной, действительно, { f 2, f 3, f 4}Î L, { f 1, f 3, f 4}Î T 1, { f 1, f 2, f 4}Î T 0, { f 1, f 2, f 3}Î M.
2 Мы знаем, что система { x 1| x 2} – полна в Р 2. Составим для нее критериальная таблица? x 1| x 2= 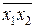 = x 1 x 2Å1.
= x 1 x 2Å1.
| Т 0 | Т 1 | L | M | S | |
| x 1| x 2 | - | - | - | - | - |
3. Составим критериальную таблицу для другой полной системы функций из Р2: из Р2: {0, 1, x 1 x 2, x 1Å x 2}.
| Т 0 | Т 1 | L | M | S | |
| + | - | + | + | - | |
| - | + | + | + | - | |
| x 1 x 2 | + | + | - | + | - |
| x 1Å x 2 | + | - | + | - | - |
Согласно критериальной таблице, полной является и система {0, 1, x 1 x 2, x 1Å x 2}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а 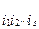 равны 0, если члены х
равны 0, если члены х  х
х  ... х
... х  , в полиноме отсутствуют.
, в полиноме отсутствуют.
4. Выясним, полна ли система  . Составим критериальную таблицу, очевидно
. Составим критериальную таблицу, очевидно  . Чтобы показать, что
. Чтобы показать, что  , достаточно найти одну функцию
, достаточно найти одну функцию  и
и  . Возьмем
. Возьмем 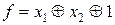 , удовлетворяющую требуемым условиям. Если f
, удовлетворяющую требуемым условиям. Если f 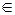 S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f
S \ T 0, то f (0,..., 0) = 1, f (1,..., 1)=0, следовательно, f 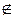 M, f
M, f 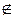 T 1. Рассмотрим функцию h = x 1 x 2
T 1. Рассмотрим функцию h = x 1 x 2  x 2 x 3
x 2 x 3  x 1 x 3=1, набор ее значений (11101000), h
x 1 x 3=1, набор ее значений (11101000), h 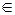 S \ T 0, но h
S \ T 0, но h 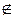 L. Следовательно, критериальная таблица имеет вид:
L. Следовательно, критериальная таблица имеет вид:
| Т 0 | Т 1 | L | M | S | |
L  T 1 T 1
| - | + | + | - | - |
| S \ T 0 | - | - | - | + | - |
и А – полная система функций.
Определение. Система функций { f 1,..., fs,...} называется базисом в Р 2,если она полна в Р 2, но любая ее подсистема не будет полной. Например, система функций { x 1& x 2, 0, 1, x 1  x 2
x 2  x 3} – базис.
x 3} – базис.
Рассмотрим набор функций f, g и h, представленный в следующей таблице:
| Функции f, g и h | |||||
| X1 | X2 | X3 | f | g | h |
Таблица 1
Функция f, очевидно, не сохраняет 0 и 1, но является самодвойственной. Функция g(X1,X2,X3)= 1+X1+X2 + X1 * X3 + X1 * X2 * X3 является несамодвойственной, немонотонной и нелинейной. По лемме 5.1 получаем, что  , функция
, функция 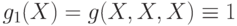 , а функция
, а функция  . Подставив X2=0 в g получим g3(X1,X3)= g(X1,0,X3)= 1 + X1 + X1 * X3. Тогда
. Подставив X2=0 в g получим g3(X1,X3)= g(X1,0,X3)= 1 + X1 + X1 * X3. Тогда  . Таким образом, мы с помощью f и g сумели выразить обе функции полной системы
. Таким образом, мы с помощью f и g сумели выразить обе функции полной системы  и, следовательно, система функций {f, g } полная.
и, следовательно, система функций {f, g } полная.
Не нашли, что искали? Воспользуйтесь поиском: