Практические задания. 1. Доказать несправедливость утверждений:

1. Доказать несправедливость утверждений:

а) «Если дифференцируемая функция у= f(x) имеет в точке х₀ вторую производную, равную нулю, то точка х₀ – точка перегиба графика функции».

б) «Если числовая последовательность ограничена, то она имеет предел».

в) «Если функция непрерывна в точке х₀, то она имеет производную в этой точке».

2. Для каждого из условий выясните, является ли оно необходимым и является ли оно достаточным, чтобы выполнялось неравенство х² – 3х – 18 £ 0: а) х=1, б) -2£ х £5, в) х³ -3, г) х> -3, д) -1£ х £ 10, е) –3 £ х £ 6.

3. Запишите на языке логики предикатов определение: «Функция f(x) называется ограниченной на множестве М, если существует такое неотрицательное число L, что для всех х ÎМ, справедливо неравенство |f(x)|£ M.»

4. В предложениях вместо многоточия поставьте слова «необходимо, но не достаточно», «достаточно, но не необходимо», «не необходимо и недостаточно», «необходимо и достаточно»:

а) Для того, чтобы четырехугольник был прямоугольным…, чтобы длины его диагоналей были равны;

б) Для того, чтобы х2 – 5х + 6 = 0…, чтобы х=3;

в) Для того, чтобы сумма четного числа натуральных чисел была четным числом, чтобы каждое слагаемое было четным;

г) Для того, чтобы окружность можно было вписать в четырехугольник, чтобы сумма длин суммы длин его противоположных сторон были равны;

д) Для того, чтобы множество было счетным, чтобы его элементы можно было записать в виде занумерованной последовательности;

е) Для того, чтобы числовая последовательность имела предел, чтобы она была ограниченной.

5.Сформулируйте:

а) Необходимый, но недостаточный признак параллелограмма;

б) Необходимый и достаточный признак параллелограмма;

в) Достаточное, но не необходимое условие, чтобы уравнение sinx = a имело решение.

г) Необходимое, но не достаточное условие, чтобы уравнение sinx = a имело решение.

Контрольные вопросы

1. Записать в виде формулы логики предикатов определение: а) непрерывности функции в точке; б) предела числовой последовательности; в) ограниченной функции.

2. Как выполняется построение противоположного утверждения к утверждению, заданному в виде формулы логики предикатов? Постройте противоположные утверждения для утверждений из первого пункта контрольных вопросов.

3. Приведите четыре вида теорем и объясните смысл каждой из них.

4. Какие из теорем являются равносильными?

5. Каким должно быть отношение между областями истинности предикатов Р(х) и Q(x), чтобы теорема 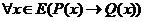была истинной? Какой в этом случае из предикатов необходимое и какой достаточное условие?

6. Какое отношение должно быть между областями истинности предикатов Р(х) и Q(x), чтобы для теоремы 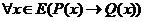была справедлива и обратная теорема? Какой теоремой можно заменить в этом случае прямую и обратную?

7. Докажите равносильность формул 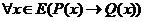и .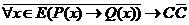

Список литературы

Не нашли, что искали? Воспользуйтесь поиском: