ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Практические задания. Задача 1. Докажите полноту системы , включающей только стрелку Пирса, непосредственно выразив через нее отрицание
Вариант 1
Задача 1. Докажите полноту системы 
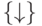, включающей только стрелку Пирса, непосредственно выразив через нее отрицание, дизъюнкцию и конъюнкцию.
Задача 2. Проверьте полноту системы функций {g, h}, представленных в таблице 1 Если она полна, выразите с помощью этих функций обе константы, отрицание 
и импликацию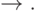 
Задача 3 Докажите, что система 
не является полной. Можно ли ее сделать полной, добавив некоторую константу?
Вариант 2
Задача 1. Определите принадлежность каждой из функций f1, f2, f3, f4 и f5, представленных в таблице 1, каждому из классов 
и 
.
Задача 2 Используя результаты задачи 1, определите, какие из троек функций, представленных в таблице 5.1, являются полными системами. Имеются ли среди них полные системы из двух функций? Из одной функции?
Задача 3. Выразите функции 
с помощью формул, построенных из функций полной системы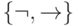 
Контрольные вопросы
1. Полнота системы функций и критерий Поста?
2. Теорема Поста (практическое применение)?
3.Базис системы функций?
Список литературы
| 1.Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с. |
| 2.Варпаховский Ф.Л. Элементы теории алгоритмов. - М., Просвещение, 1970. - 25 с. (МГЗПИ) |
| 3.Гуц А.К. Математическая лоrика и теория алrоритмов. - Омск: Издательство Наследие. Диалог-Сибирь, 2003. - 108 с. |
| 4.Босс В. Лекции по математике. Т. 6: От Диофанта до Тьюринга. - М.: КомКнига, 2006. - 208 с. |
| 5.Босс В. Лекции по математике. Т. 10: Перебор и эффективные алгоритмы: Учебное пособие. — М.: Издательство ЛКИ, 2008. - 216 с. |
Не нашли, что искали? Воспользуйтесь поиском: