Необходимые и достаточные условия.

Рассмотрим теорему

Множество истинности предиката Р(х) ® Q(x) есть множество CIp U Iq. Но тогда множеством ложности этого предиката будет C(С1р U Iq)= Iр Ç CI_Q. Последнее множество будет пустым лишь в случае, когда Iр Ì Iq.

Итак, предикат Р(х) ® Q(x) является истинным для всех х Î Е в том и только в том случае, когда множество истинности предиката Р(х) содержится в множестве истинности предиката Q(x). При этом говорят, что предикат Q(x) логически следует из предиката Р(х), и предикат называют необходимым условием для предиката Р(х), а предикат Р(х) - достаточным условием для Q(x). Так, в теореме «Если х - число натуральное, то оно целое» предикат Q(x):«х - число целое» логически следует из пре­диката Р(х): «х – число натуральное», а предикат «х - число натуральное» является достаточным условием для предиката «х - число целое».

Часто встречается ситуация, при которой истинные взаимно обратные теоремы:

Это возможно при условии, что Ip = Iq, т.к. одновременно выполняются два условия: I_PÌI_Q и I_QÌI_P. В таком случае из теоремы(1) следует, что условие Р(х) является достаточным для Q(x), а из теоремы(2) следует, что условие Р(х) является необходимым для Q(x).

Таким образом, если истинны теоремы (1) и (2), то условие Р(х) является и необходимым, и достаточным для Q(x). Аналогично в этом случае условие Q(x) является необходимым и достаточным для Р(х).

Иногда вместо логической связки «необходимо и достаточно» употребляют логическую связку «тогда и только тогда».

Так как здесь истинны высказывания(1) и (2), то истинно высказывание:

Рассмотрим примеры.

1) Теорема «Если число l делится на 12, то оно делится на 3» истинна. Поэтому здесь делимость числа l на 12 является достаточным условием для делимости числа l на 3, а делимость числа l на 3 является необходимым условием для делимости числа l на 12. В то же время обратная теорема «Если число l делится на 3, то оно делится на 12» не верна. Поэтому делимость числа l на 3 не является достаточным условием делимости числа l на 12, а делимость числа l на 12 не является необходимым условием делимости числа l на 3.

2) Теоремы «В описанном четырехугольнике суммы длин противоположных сторон равны между собой» и «Если в четырехугольнике суммы длин противоположных сторон равны между собой, то в этот четыреху­гольник можно вписать окружность» взаимно обратны. Обе они истинны, и, следовательно, здесь можно употребить логическую связку «необходимо и достаточно»:

«Для того, чтобы в четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы длин его противоположных сторон были равны между собой».

3) Для каждого из условий выясните, является ли оно необходимым и является ли оно достаточным, чтобы выполнялось неравенство х² – 2х – 8 £ 0: а) х=0, б) -1£ х £3, в) х³ -3, г) х> -2, д) -1£ х £ 10, е) –2 £ х £ 4.

Неравенство перепишем в виде (х+2)(х-4)£ 0, его решением являются хÎ[-2, 4].

а) х=0 – достаточное условие для выполнения неравенства, т.к. 0Î[-2, 4].

б) [-1, 3]Ì [-2, 4]. Значит -1£ х £3 – достаточное условие.

в) [-3, +¥)É[-2, 4], следовательно, является необходимым условием.

г) (-2, +¥)Ë[-2, 4] и [-2, 4]Ë(2, +¥), значит, не является ни необходимым, ни достаточным условием.

д) [-1, 10] Ë[-2, 4] и [-2, 4]Ë [-1, 10], значит, не является ни необходимым, ни достаточным условием.

е) [-2, 4]=[-2, 4], следовательно, является и необходимым и достаточным условием.

5. Доказательство методом от противного.

не верна, то есть существует такой объект х, что условие Р(х) истинно, а заключение Q(x) - ложно. Если из этих предположений путем логических рассуждений приходят к противоречивому утверждению, то делают вывод о том, что исходное предположение не верно, и верна теорема(1).Покажем, что такой подход дает доказательство ис­тинности теоремы(1).

Действительно, предположение о том, что теорема (1) не справедлива, означает истинность формулы

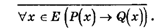
Противоречивое утверждение, которое получается из допущенного предположения, есть конъюнкция С& , где С — некоторое высказывание. Таким образом, схема доказательства от противного сводится к доказательству истинности формулы

Легко видеть, что эта формула равносильна фор­муле(1).

Действительно,

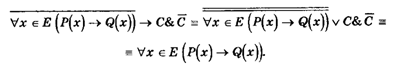
Не нашли, что искали? Воспользуйтесь поиском: