
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Поперечно-строгального станка
1.2 Звено – это деталь или несколько деталей, жестко связанных между собой и движущихся в механизме как одно целое.
Подвижные звенья обозначены на рис. 1.1 цифрами 1…5, неподвижное звено (стойка) цифрой 0. Подвижные звенья: 1 - кривошип, совершающий вращение вокруг точки О1 с постоянной частотой n1; 2 – кулиса, совершающая плоскопараллельное движение; 3 – камень, вращающийся вокруг точки О3; 4 – камень, движущийся поступательно; 5 – ползун, движущийся возвратно-поступательно. Входным звеном является кривошип 1, соединенный с приводом. Выходным звеном – ползун 5, с которым связан режущий инструмент поперечно-строгального станка. Механизм предназначен для преобразования вращательного движения кривошипа в возвратно-поступательное перемещение ползуна.
1.3 Кинематическая пара – это соединение двух соприкасающихся звеньев, допускающее их относительное движение. В данном механизме 7 кинематических пар. Все они являются низшими (их элементы – поверхности), высшие КП отсутствуют.
В данном механизме это кинематические пары:
| Обозначение | О1 | А | В | О3 | С | С′ | D |
| Соединяемые звенья | 0-1 | 1-2 | 2-3 | 3-0 | 2-4 | 4-5 | 5-0 |
| Класс | |||||||
| Вид | Вращ. | Вращ. | Пост. | Вращ. | Вращ. | Пост. | Пост. |
1.4 Число степеней свободы плоского механизма определим по формуле Чебышева

где 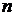 – число подвижных звеньев,
– число подвижных звеньев, 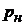 – число низших кинематических пар,
– число низших кинематических пар,  – число высших кинематических пар.
– число высших кинематических пар.
В нашем механизме  =0, поэтому
=0, поэтому  3∙5 – 2∙7 = 1, то есть одна обобщенная координата определяет положение всех звеньев механизма. Следовательно, должно быть одно входное звено.
3∙5 – 2∙7 = 1, то есть одна обобщенная координата определяет положение всех звеньев механизма. Следовательно, должно быть одно входное звено.
1.5 Любой механизм может быть образован путем последовательного присоединения к одному или нескольким начальным звеньям и стойке кинематических групп (групп Ассура) с нулевой сетью подвижности относительно тех звеньев, к которым группа присоединяется. Начальное звено – это звено, которому приписывается обобщенная координата. Это звено, образующее со стойкой кинематическую пару 5-го класса.

| 
| 
|
| Рис. 1.2. Группа 4-5 W = 3×2 – 2×3=0. Класс 2-ой, порядок 2-ой. | Рис. 1.3. Группа 2-3 W = 3×1 – 2×1=1 Класс 2-ой, порядок 2-ой. | Рис.1.4. Начальное звено Класс 1-ый, порядок 1-ый |
Структурная группа не изменяет числа степеней свободы механизма, к которому она присоединяется, то есть  , откуда
, откуда  . Последнее условие выполняется, если
. Последнее условие выполняется, если 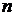 = 2,4,6…, а
= 2,4,6…, а  …. Самая простая структурная группа состоит из двух звеньев и трех кинематических пар (
…. Самая простая структурная группа состоит из двух звеньев и трех кинематических пар (
 ). Это группа называется группой II класса, 2-го порядка. Порядок группы определяется числом свободных кинематических пар, которыми она может присоединяться к механизму.
). Это группа называется группой II класса, 2-го порядка. Порядок группы определяется числом свободных кинематических пар, которыми она может присоединяться к механизму.
Выделим группы Ассура согласно приведенному соотношению 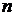 и
и 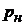 , начиная с наиболее удаленных звеньев от начального звена. Изобразим группы Ассура и начальное звено.
, начиная с наиболее удаленных звеньев от начального звена. Изобразим группы Ассура и начальное звено.
1.6. Предложенный механизм является плоским шарнирно-рычажным механизмом, имеет одну степень свободы, состоит из двух структурных групп и начального звена. Класс механизма определяется наивысшим классом, входящих в него структурных групп. Рассматриваемый механизм – 2-го класса.
1.7. Число избыточных связей определяем по формуле 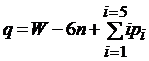 , где
, где  =1…5, или для заданного механизма
=1…5, или для заданного механизма  .
.
1.8. Устраним избыточные связи, понизив классы кинематических пар. Чтобы обеспечить  , необходимо иметь для плоского механизма соотношение
, необходимо иметь для плоского механизма соотношение
0=1 – 6 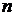 +5
+5  +4
+4  +3
+3  , откуда 6
, откуда 6 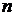 – 1 = 5
– 1 = 5  +4
+4  +3
+3  . При
. При 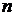 =5 имеем
=5 имеем
5  +4
+4  +3
+3  =29.
=29.
Вторым уравнением является условие неизменности числа кинематических пар:  +
+  +
+  =7.
=7.
Первое равенство должно быть выполнено в механизме без избыточных связей, что обеспечивается  =3,
=3,  =2,
=2,  =2 и 5×3 + 4×2 + 3 + 2 = 29 или
=2 и 5×3 + 4×2 + 3 + 2 = 29 или  = 4,
= 4,  = 0,
= 0,  = 3 и 5×4 + 4×0 + 3×3 = 29. В обоих случаях число кинематических пар 3 + 2 + 2 = 7 и 4 + 3 = 7.
= 3 и 5×4 + 4×0 + 3×3 = 29. В обоих случаях число кинематических пар 3 + 2 + 2 = 7 и 4 + 3 = 7.
Более рациональным служит первое соотношение  = 3,
= 3,  = 2,
= 2,  = 2.
= 2.
При понижении класса кинематических пар следует иметь в виду: как правило не понижается класс кинематических пар, образованных подвижными звеньями со стойкой ( ,
,  ) и поступательных пар.
) и поступательных пар.
Понизим класс кинематических пар. Схема соответствующего механизма показана на рис. 1.5.
Примечание. Формальное устранение избыточных связей по уравнениям не всегда гарантирует их конструктивное исполнение. Так, невозможность применения пары 4-го класса в соединении звеньев 4-5 приводит к тому, что в контуре 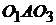 имеется лишняя степень свободы, тогда в контуре
имеется лишняя степень свободы, тогда в контуре  появляется одна избыточная связь.
появляется одна избыточная связь.

Рис. 1.5. Схема механизма поперечно-строгального
станка без избыточных связей
Пример 2
1.1. Рассмотрим схему кулисного механизма брикетировочного автомата. Изобразим структурную схему (рис.1.6).
1.2. Подвижные звенья: 1 – кривошип (вращение вокруг точки  ); 2 – камень (плоскопараллельное движение); 3 – кулиса (возвратно - вращательное движение); шатун (плоскопараллельное движение); 5 – ползун (возвратно-поступательное движение).
); 2 – камень (плоскопараллельное движение); 3 – кулиса (возвратно - вращательное движение); шатун (плоскопараллельное движение); 5 – ползун (возвратно-поступательное движение).
Подвижных звеньев 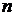 = 5.
= 5.
Входное звено 1 – кривошип, выходное – ползун 5.
1.3 Кинематические пары.
| Обозначение | О1 | A | B | О3 | C | D | D΄ |
| Соединение звеньев | 0-1 | 1-2 | 2-3 | 3-0 | 3-4 | 4-5 | 5-0 |
| Класс | |||||||
| Вид | Вращ. | Вращ. | Пост. | Вращ. | Вращ. | Вращ. | Пост. |
Всего кинематических пар 7, все низшие.
1.4. 

Рис. 1.6. Структурная схема механизма брикетировочного автомата
1.5. Группы Ассура и начальное звено.

| 
| 
|
Рис. 1.7. Группа 4-5
W =3 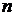 –2 –2 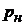 =3×2–2×3=0.
Класс 2-ой,
порядок – 2-ой. =3×2–2×3=0.
Класс 2-ой,
порядок – 2-ой.
| Рис. 1.8. Группа 2-3
W =3 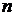 –2 –2 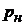 =3×2–2×3=0.
Класс 2-ой,
порядок – 2-ой. =3×2–2×3=0.
Класс 2-ой,
порядок – 2-ой.
| Рис.1.9 Начальное звено
W =3 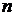 -2 -2 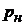 =3×2-2×1=1
Класс 1-ый,
порядок 1-ый. =3×2-2×1=1
Класс 1-ый,
порядок 1-ый.
|
1.6. Механизм шарнирно-рычажный, плоский, 2-го класса. Имеет одну степень свободы. Состоит из двух структурных групп и начального звена.
1.7. Избыточные связи:  , где
, где  =1…5, или для
=1…5, или для
заданного механизма  .
.
Принимаем соотношение 5  +4
+4  +3
+3  =29, получаемое при
=29, получаемое при  =3,
=3,  =2,
=2,  =3.
=3.
1.8. Понижаем класс кинематических пар соединений звеньев 0-3, 4-5 до 3-его; 1-2, 2-4 до 4-го. Схема механизма при  =0 показана на
=0 показана на
рис. 1.10.

Рис. 1.10. Схема механизма брикетирования без избыточных связей
Пример 3
1.1 Схема механизма компрессора (рис.1.11).
1.2. Подвижные звенья:
1 – кривошип (вращение вокруг точки О1); 2 – шатун (плоскопараллельное движение); 3 – коромысло (возвратно-вращательное движение); 4 – шатун (плоскопараллельное движение); 5 – ползун (возвратно-поступательное движение).
Подвижных звеньев n = 5.
Входное звено 1 – кривошип, выходное – ползун 5.
Механизм предназначен для преобразования вращательного
движения кривошипа в возвратно-поступательное движение ползуна.
1.3. Кинематические пары.
| Обозначение | О1 | A | B | О3 | C | D | D΄ |
| Соединение звеньев | 0-1 | 1-2 | 2-3 | 3-0 | 3-4 | 4-5 | 5-0 |
| Класс | |||||||
| Вид | Вращ. | Вращ. | Вращ. | Вращ. | Вращ. | Вращ. | Пост. |
Всего кинематических пар 7, все низшие.
1.4. 

 ,
,  Тогда W = 1.
Тогда W = 1.
В механизме одно ведущее звено (кривошип 1).

Рис. 1.11. Структурная схема механизма компрессора
1.5. Группы Асура и начальное звено.

| 
| 
|
Рис. 1.12. Группа 4-5
 Класс 2-ой,
порядок – 2-ой.
Класс 2-ой,
порядок – 2-ой.
| Рис. 1.13. Группа 2-3
 Класс 2-ой,
порядок – 2-ой.
Класс 2-ой,
порядок – 2-ой.
| Рис. 1.14 Начальное звено
 Класс 1-ый,
порядок 1-ый
Класс 1-ый,
порядок 1-ый
|
1.5. Механизм шарнирно-рычажный, плоский, 2-го класса.
1.6. Избыточные связи q = W -6 n +5 p5 =1-6×5+5×7=6.
1.7. Принимаем соотношение 5р5+4р4+3р3=29, получаемое при р5 =3, р4 =2, р3 =2. Понижаем класс кинематических пар, например, соединений звеньев 4-5, 2-3 до 3-его, 1-2, 3-4 – до 4-го. Получаем схему механизма (рис. 1.15).

Рис. 1.15. Схема механизма компрессора без избыточных связей
Не нашли, что искали? Воспользуйтесь поиском: