Первая и вторая теорема Шеннона для источников без памяти

Первая теорема Шеннона

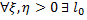такое, что при l>l₀ все реализации длины l источника [A, p(S)] могут быть разбиты на 2 класса

таких, что для последовательности 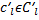имеет место неравенство

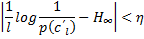
Где 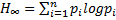– энтропия источника.

Суммарная вероятность последовательностей из 2-го класса <ε

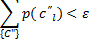
Следствие 1) Оценивается:

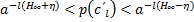, а – основание логарифма

Следствие 2) Суммарная вероятность последней из первого класса не менее 1-ε:

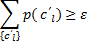
Упорядочим все последовательности длины l, полученные из источника без памяти, по убыванию их вероятностей. Пусть 0<α<1. Будем отбирать наиболее вероятные последовательности, пока их суммарная вероятность, оставаясь меньше заданного α, не будет обладать следующим свойством: добавление у этой сумме вероятности реализации следующей последовательности делает её больше α. Множество отобранных последовательностей обозначим M_I(α).

Вторая теорема Шеннона.

Для класса M_I(α) высоковероятных последовательностей, реализуемых на источнике без памяти [A, p(S)], определяемого заданным уровнем α: 0<α<1 имеет место следующее равенство:

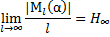
Не нашли, что искали? Воспользуйтесь поиском: