Теоремы Шеннона для Марковских источников.

1 теорема Шеннона для Марковских источников.

m=1.

Для любых и существует такое, что при 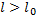все реализации длины источника могут быть разбиты на 2 класса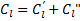

Энтропия источника: причем

2 теорема Шеннона для Марковских источников

Для любых и существует такое, что при 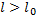все реализации длины источника могут быть разбиты на 2 класса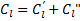

Энтропия источника:

Марковский источник обладает свойством информационной устойчивости, что позволяет оценить число последних вошедших в 1-ый класс.

Эргодические источники

(*)

Дискретный стационарный источник [A,p(s)] называется эргодическим, если любое измеримое относительно вероятностной меры p(s), заданной на Fs, инвариантное по сдвигу множество последовательностей, порождённых источником, имеет вероятность либо единица, либо нуль.

Эргодические источники являются наиболее близкими с вероятностной точки зрения моделями осмысленных сообщений. Поэтому формулу (*) можно рассматривать как оценку числа литературных текстов длины l, в алфавите А, где H∞ понимается как энтропия текста на один знак.

Не нашли, что искали? Воспользуйтесь поиском: