Теоремы Мак-Милана.

Пусть последовательность C _l порождена дискретным стационарным эргодическим источником [A,P (S)]. Тогда для произвольных ε>0, δ>0 существует целое число l₀( ε, δ ) такое, что при l> l₀( ε, δ )

(1)

Где p(c _l) – вероятность реализации последовательности

c _l =a_i1,…, a_{i l ,} а H∞- энтропия источника.

Доказательство:

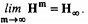
для любого ε > 0 и соответствующего δ’ > 0 для m > m₀(ε) и l > m будет выполняться:

на любителя:

Полагая δ’= δ/3 получаем, что для достаточно больших l будет выполняться неравенство (1), что и доказывает теорему Мак-Миллана.

Имеет место свойство информационной устойчивости. Собственная информация последовательности, порождённой эргодическим стационарным источником, удовлетворяет соотношению:

Используем эту вероятностную трактовку соотношения. Последовательности, порождённые стационарным эргодическим источником, обладают свойством равнораспределённости

Свойство равнораспределённости позволяет оценить количество последовательностей, порождённых источником такого типа:

(*)

Оптимальное кодирование. Основные понятия и определения.

Рассмотрим схему передачи информации от источников сообщений:

Чтобы эффективнее и экономичнее использовать канал связи, следует так преобразовывать порожденную информацию, чтобы на ее передачу по каналу затрачивалось минимально возможное время. Такое преобразование информации называется кодированием источников сообщений.

В настоящее время эта задача решена для источников без памяти.

Источник: [А; p(S)], A=(a₁…a_n). Кодер [В; p(S)] для источника обладает алфавитом B=(b₁…b_D), |B|=D - мощность.

Кодирование – отображение φ: a_i→ =(b_j1…b_jk), где – кодовое слово.

При этом, если a_i≠a_j, то ≠ .

Совокупность всех кодовых слов { }– код.

Код равномерный (блоковый), если длины всех кодовых слов равны, и неравномерный в противном случае.

Код однозначно декодируемый (разделимый), если существует метод однозначного разделения на отдельные кодовые слова последовательности букв алфавита В, полученные на входе декодера.

Рассмотрим кодовое слово =(b_j1…b_jl), начальная часть этого слова b_j1…b_ji, где i= – префикс.

Говорят, что код является префиксным, если никакое кодовое слово не совпадает с началом другого кодового слова. Всякий префиксный код однозначно декодируемый.

Преимущество: декодирование осуществляется без задержек в ходе поступления букв алфавита в декодер.

Не нашли, что искали? Воспользуйтесь поиском: