Свойства оптимального кода.

Свойства оптимального кода: Рассмотрим источник кодирования, с вероятностями 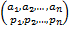, причем .Необходимо построить двоичный код с минимальной средней длиной.

Рассмотрим свойства оптимального кода для вероятностных распределений на алфавите А, отличного от равномерного.

Свойства:

1. В оптимальном коде длины кодовых слов не убывают.

2. Существует оптимальный префиксный код, в котором двум, наименее вероятным буквам 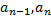, соответствуют кодовые слова, имеющие одинаковую длину и различающиеся лишь в последнем разряде.

Построим новый источник A’, полученный из исходного источника A склеиванием наименее вероятных букв в букву a’ в источнике A’. Буквы порождаются с вероятностями совпадающими с вероятностями этих букв в источнике A, а буква a’ имеет вероятность равную сумме вероятностей (). Новый источник называется редуцированным, а операцию его получения редуцированием, эту операцию можно проводить конечное число раз, до тех пор, пока алфавит источника не будет состоять из 1 буквы, порождаемой с вероятностью 1. Имея код, отвечающий редуцированному источнику A’ можно построить код, отвечающий исходному источнику А.

Пусть буквам алфавита A’ сопоставлены кодовые слова тогда для алфавита A построим код следующим образом: для букв сохраним кодовые слова , а в качестве 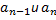кодовых слов возьмём слова, полученные в результате дописывания к кодовому слову символов 0 и 1 соответственно.

3. Если префиксный код, для редуцированного источника A’, является оптимальным, то и код, для исходного источника A, построенного указанным способом, также будет оптимальным.

Алгоритм Хаффмана.

Алгоритм Хаффмана для двоичной системы исчисления ( ): Этот алгоритм приводит к построению оптимального множества кодовых слов, в том смысле, Что никакое другое множество не имеет меньшего среднего числа символов на букву алфавита А. Для любого источника все наборы кодовых слов, удовлетворяющие свойствам 1-3, дают одну и ту же среднюю длину кодового слова. Этот алгоритм позволяет построить, по крайней мере, один из таких наборов. Последовательная реализация свойств 1-3 и есть суть метода Хаффмана.

Алгоритм Хаффмана сводится к выполнению 2-х частей алгоритма:

1. Построение последовательностей редуцированных источников сходящихся к вырожденному источнику.

1) Буквы источника располагают в порядке убывания вероятностей.

2) Две наименее вероятные буквы склеиваются в 1 букву редуцированного источника и приписывают этой букве суммарную вероятность склеенных букв.

3) Переходят к 1-у пункту, если алфавит редуцированного источника состоит из 2-х или более букв, в противном случае переходят ко 2-ой части.

2. Построение кодового дерева и соответствующего оптимального кода.

Проводят ребра, соединяющие буквы в алфавитах последовательных редуцированных источников и получаем граф дерева, в котором буквы исходного источника являются концевыми вершинами дерева, а единственная буква последнего вырожденного источника соответствует корню дерева. Помечают построенные ребра метками из алфавита и прослеживают эти метки при движении от корня дерева к концевой вершине. В итоге получают кодовое слово, соответствующее букве исходного алфавита. Полученный код является префиксным.

Приведенный алгоритм приводит к оптимальному множеству кодовых слов, за исключением, когда в исходном источнике или последующих редуцированных источниках имеется более 2-х букв с равными и минимальными вероятностями. Располагая в другом порядке буквы редуцированных алфавитов можно получить оптимальные префиксные коды с наборами кодовых слов тех же длин, что и в рассмотренном примере, коды будут отличаться лишь кодовыми словами.

Не нашли, что искали? Воспользуйтесь поиском: