Двоичный симплексный код к коду Хэмминга.

Является методом построения двоичного кода исправляющего 1 ошибку. Синдром, принятого вектора равен линейной комбинации тех столбцов проверочной матрицы () номера которых совпадают с номерами искаженных компонент, а коэффициенты линейной комбинации равны величинам ошибок, поэтому проверочная матрица кода исправляющего ошибку должна удовлетворять 2-м ограничениям:

1. Матрица H не должна иметь 0 столбцов.

2. Все столбцы матрицы должны быть различными.

В противном случае ошибки не будут выявляться.

Пусть число строк проверочной матрицы 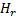. Чтобы построить код с максимально возможной скоростью передачи данных () возьмем все допустимые не нулевые двоичные векторы столбцы из векторного пространства , для построения матрицы будем выписывать их в порядке возрастания чисел.

Двоичный код с длиной блока проверочной матрицы образованный всеми не нулевыми векторами из векторного пространства , расположенными в порядке возрастания чисел, двоичные разложения которых совпадают с рассматриваемыми столбцами называется двоичным кодом Хемминга. Обозначается .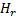

Длина кодового слова ; количество информационных символов .

Процедура декодирования для кодов Хемминга имеет вид: пусть произошла ошибка в символе кодового слова , подсчитаем синдром полученного вектора . Тогда синдром будет иметь вид . Если произошла 1 ошибка, то синдром в двоичной записи указывает номер столбца, в котором произошла ошибка. Из свойств кода исправлять ошибку следует, что кодовое расстояние .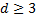

Теорема: коды Хемминга являются совершенными.

Коды Хемминга распространяются на любую систему счисления. Длина кода характеризуется числом , где - число строк проверочной матрицы и , -простое число.

Двоичным симплексным кодом () называют код, двойственных коду Хемминга. По определению двойственного кода порождающая матрица кода Хемминга является проверочной для двоичного симплексного кода, проверочная матрица кода Хемминга 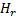является порождающей для двоичного симплексного кода. Для построения двоичного симплексного кода используют индуктивный метод.

Каждая пара кодовых слов симплексного кода находится друг от друга на одинаковом расстоянии, такие коды называются эквидистантными. Все слова симплексного кода, за исключением нулевого, имеют одинаковый вес, т.е. симплексный код является равновесным. Симплексные коды распространяются на все системы счисления. Параметры кода:

– число проверочных символов

– кодовое расстояние

Методы построения новых кодов. Методы: добавление общей проверки на четность; выкалывание кодовых координат.

1. Добавление общей проверки на четность.

Пусть линейный код с кодовым расстоянием , в котором имеются кодовые слова нечетного веса. Для каждого вектора из этого кода с координатами вычисляем .

Рассмотрим новый код

Проверочная матрица имеет вид:

Свойства синдрома :

1. Если ошибок при передаче нет, то синдром равен 0 ();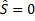

2. Если 1 ошибка, то синдром имеет первую компоненту 1, а остальные r компонент задают двоичное разложение номера искаженной позиции.

3. Если ошибок 2, то общая проверка на четность равна 0, некоторые компоненты будут отличны от 0 и необходима повторная передача.

2. Выкалывание новых координат.

Из всех кодовых векторов, одновременно, удаляется 1 или более одноименных координат. Например: при удалении 1 координаты

Методы построения новых кодов. Методы: построение кода выбрасыванием слов, пополнение кода путем добавления новых слов, удлинение кода добавлением информационных символов, усечение кода.

3. Построение кода выбрасыванием слов.

Пусть исходный код G содержит векторы четного и нечетного веса. Слова нечетного веса образуют класс смежности по множеству векторов четного веса. Удалим из G все векторы нечетного веса, получим код со следующими характеристиками:

4. Добавление новых кодовых слов.

Пусть единичный вектор не принадлежит коду G. Добавляя к коду G множество , получим:

-наибольший вес

5. Удлинение добавлением информационных символов.

6. Последовательно получаем . Параметры: .Укорачивание кода. Выбираются все векторы, первая координата которых равна 0. Код G’ составляется из этих векторов после удаления первой координаты, его характеристики:

Методы построения новых кодов. Методы: построение кода с помощью прямой суммы, построение кода с помощью полупрямой суммы, произведение кодов.

7. Построение кода с помощью прямой суммы.

Пусть параметры:

8. Построение кодов с помощью полупрямой суммы.

Пусть 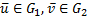, тогда характеризуется

9. Произведение кодов.

Пусть - систематический код Запишем в виде матрицы.

троки этой матрицы закодируем кодом , в результате в каждой строке матрицы будет добавлено проверочных символов, удовлетворяющих проверочным символам.

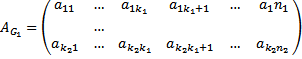
ждый столбец закодируем с помощью линейного систематического кода .

Выписывая элементы этой матрицы по строчкам получим кодовый вектор, соответствующий исходному информационному вектору, эту процедуру повторяем для каждого информационного вектора. В итоге получается код: , с характеристиками:

ОПРЕДЕЛЕНИЯ

1. Дискретный источник сообщений.

Под ДИС понимают устройство, порождающее последовательности, составленные из букв конечного алфавита А, мощностью n<∞. При этом буквы последовательности порождаются в дискретные моменты времени.

2. Стационарный источник сообщений.

Если вероятность того, что источник [A, p(S)] порождает некоторую последовательность ai1, …, ail, составленную из букв алфавита A в моменты времени 1, 2, …, l равна вероятности того, что попрождается точно такая же последовательность в моменты времени j+1, …, j+l для любых j, l, последовательности букв (ai1,…, ail), то источник называется стационарным.

3. Источник без памяти.

Если вероятность того, что источник [A, p(S)] порождает некоторую последовательность ai1, …, ail, составленную из букв алфавита A в моменты времени 1, 2, …, l равна вероятности того, что попрождается точно такая же последовательность в моменты времени j+1, …, j+l для любых j, l, последовательности букв (ai1,…, ail), то источник называется стационарным.

4. Марковский источник

Дискретный стационарный источник называется Марковским порядка m, если для любого и любой последовательности выполняется, что вероятность появления .

5. Энтропия марковского источника

Энтропией Марковского источника называется величина:

Энтропия Марковского источника всегда существует в силу теоремы Вейер-Штрасса.

6. Эргодический источник

(*)

Дискретный стационарный источник [A,p(s)] называется эргодическим, если любое измеримое относительно вероятностной меры p(s), заданной на Fs, инвариантное по сдвигу множество последовательностей, порождённых источником, имеет вероятность либо единица, либо нуль.

Эргодические источники являются наиболее близкими с вероятностной точки зрения моделями осмысленных сообщений. Поэтому формулу (*) можно рассматривать как оценку числа литературных текстов длины l, в алфавите А, где H∞ понимается как энтропия текста на один знак.

7. Кодирование.

Рассмотрим схему передачи информации от источников сообщений:

Чтобы эффективнее и экономичнее использовать канал связи, следует так преобразовывать порожденную информацию, чтобы на ее передачу по каналу затрачивалось минимально возможное время. Такое преобразование информации называется кодированием источников сообщений

8. Код

правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов). Кодом также называется отдельная комбинация таких символов (знаков) — слово. Для различия этих терминов, код в последнем значении ещё называется кодовым словом.

9. Равномерный (блоковый) код

Код равномерный (блоковый), если длины всех кодовых слов равны, и неравномерный в противном случае.

10. Однозначно декодируемый код однозначно декодируемый (разделимый), если существует метод однозначного разделения на отдельные кодовые слова последовательности букв алфавита В, полученные на входе декодера.

Префикс

Рассмотрим кодовое слово =(b_j1…b_jl), начальная часть этого слова b_j1…b_ji, где i= – префикс.

12.Префикс

Говорят, что код является префиксным, если никакое кодовое слово не совпадает с началом другого кодового слова. Всякий префиксный код однозначно декодируемый.

Преимущество: декодирование осуществляется без задержек в ходе поступления букв алфавита в декодер.

12. Кодовое дерево

Не нашли, что искали? Воспользуйтесь поиском: