Статическая проводимость

Имея в распоряжении выражение (7.3.12) нетрудно рассчитать плотность тока в металлах и полупроводниках в постоянном электрическом поле E.

Металлы

Плотность тока J определяется выражением

.(7.4.1)

Сила F в (6.3.12), действующая на электрон в электрическом поле равна . Тогда для стационарной плотности тока, получаем

. (7.4.2)

В этом случае проводимость, характеризующая отклик электрона на внешнее поле определяется тензором статической проводимости и определяется соотношением

,

и имеет следующий вид

. (7.4.3)

Наличие производной по энергии от функции распределеиия в этом интеграле удобнее перейти к интегрированию по поверхности постоянной энергии с помощью замены

, (7.4.4)

где dS – элемент поверхности постоянной энергии E, перпендикулярный к нормали этой поверхности (см. рис)

Такая замена связана с тем, что производная от функции распределения ведёт себя как – функция с центром при энергии Ферми , симметричную относительно 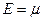, и имеющего ширину , как показано на рис.

Тогда тензор электропроводности можно представить в виде

, (7.4.5)

где интеграл берётся по изоэнергетической поверхности с энергией Ферми.

Как уже отмечали в изотропных материалах, например, с кубической симметрией, выражения для плотности тока не зависят от направления поля и, следовательно, не меняется при усреднении по всем направлениям поля относительно кристаллических осей. Усреднение выражения плотности тока добавляет множитель 1/3. Тогда

(7.4.6)

Отсюда следует, что тензор статической электропроводности становится скаляром

, (7.4.7)

где – площадь поверхности Ферми, – среднее время релаксации, 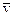– средняя скорость на поверхности Ферми, – усреднённое по поверхности Ферми значение длины свободного пробега. Формула (7.4.7) представляет стандартное выражение для статической проводимости в изотропных материалах, справедливое при любой форме поверхности Ферми. Из него также следует, что материалы, у которых поверхность Ферми отсутствует – её площадь равна нулю, их проводимость также равна нулю. Как мы знаем, таким свойством обладают полупроводники и диэлектрики.

Полупроводники

Электронный газ в полупроводниках является невырожденной системой и поэтому функция распределения мала, т. е. . В этом случае удобнее начать вычисление электропроводности с интеграла столкновений, что приводит нас к выражению

. (7.4.8)

Учитывая, что функции распределения удовлетворяет условию и соотношение для среднего значения тепловой энергии

Для проводимости можно написать

, (7.4.9)

где

(7.4.10)

Есть усреднённое по энергетическому распределению время релаксации. Выражение (6.4.9) часто записывают в виде

, (7.4.11)

где – подвижность электронов (дрейфовая скорость в единичном поле). Если проводимости тока участвуют электроны и дырки одновременно, их электропроводность суммируется, так как оба вклада пропорциональны квадрату заряда

. (7.4.12)

Это соотношение справедливо, если оба типа носителей имеют одинаковое время релаксации. Заметим, что проводимость всегда имеет положительный знак, не зависящий от знака носителей тока. Для полупроводников с собственной проводимостью выражение (6.4.12) можно упростить. Поскольку – то

Температурная зависимость величины для полупроводников с собственной проводимостью определяется, следовательно, двумя факторами: температурной зависимостью числа электронов проводимости, переброшенных через запрещённую зону, и характером изменения подвижностей носителей тока с температурой.

В общем случае подвижность (иэлектропроводность ) в полупроводниковых кристаллахявляется тензором. Но так как в кристаллах типа кремния и германия имеются симметричные эквивалентные долины в энергетическом спектре, то подвижность (и электропроводность) усредняется и оказывается изотропной

,

где – подвижность (проводимость) электронов по одному из направлений.

Не нашли, что искали? Воспользуйтесь поиском: