Краткие теоретические сведения. Переменная величина, принимающая в результате испытания то или иное (но при этом только одно) возможное значения в зависимости от случая

Переменная величина, принимающая в результате испытания то или иное (но при этом только одно) возможное значения в зависимости от случая, называется случайной величиной (СВ).

Различают дискретные (ДСВ) и непрерывные (НСВ) случайные величины.

Значения дискретной случайной величины изолированы друг от друга, в то время как непрерывная случайная величина принимает любые значения из некоторого интервала.

СВ обозначаются заглавными буквами X, Y, Z,… Значения случайных величин обозначают соответственно буквами x, y, z,…

Например, стрелок стреляет по мишени. Рассмотрим случайные величины:

X - число выбитых очков, и У - отклонение от центра мишени.

Здесь X - ДСВ, принимающая одно из одиннадцати возможных значений: 0, 1, 2, 3,..., 10.

У - НСВ, принимающая значения в интервале [0;+∞).

Для задания СВ недостаточно перечислить все ее возможные значения или записать интервал возможных значений, необходимо также указать как часто эти значения встречаются.

Полную информацию о ДСВ дает ее закон распределения. Для ДСВ, чаще всего, используют таблицу, где в верхней строке записываются в возрастающем порядке все возможные значения СВ, а в нижней строке - вероятности, с которыми эти значения встречаются:

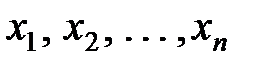- значения случайной величины X, причем х ₁ < х ₂ <... < х_n; , т.е. - вероятность того, что случайная величина X приняла значение , i = 1, 2,..., п.

Закон распределения дискретной случайной величины иначе называют рядом распределения.

Если закон распределения дискретной случайной величины составлен правильно, то должно выполняться равенство: .

Для задания НСВ чаще всего применяют функцию плотности распределения , которая обладает следующими свойствами:

1^о. , т.е. кривая функции плотности расположена либо выше оси абсцисс, либо на ней.

2^о. , геометрически это означает, что площадь, ограниченная кривой плотности распределения и осью абсцисс равна единице.

3^о. Вероятность того, что НСВ заключенное в интервале 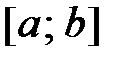, равна определенному интегралу от функции плотности на этом интервале, т.е. .

Закон распределения содержит полную информацию о случайной величине, однако для практического использования эта полная информация часто не обязательна, достаточно знать некоторые числовые характеристики, отражающие основные свойства распределения данной случайной величины.

К основным числовым характеристикам случайной величины X относятся математическое ожиданиеМ(Х), дисперсияD(Х) и среднее квадратическое отклонениеσ(Х).

Математическое ожидание М(Х) определяется формулой:

для ДСВ – , (2.1)

для НСВ – . (2.2)

Математическое ожидание характеризует центр распределения, около которого сосредоточены все возможные значения СВ, т.е. определяет среднее значение.

Дисперсией D(Х) называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.:

. (2.3)

Если преобразовать правую часть формулы (2.3), используя свойства математического ожидания, то получим следующую формулу:

, (2.4)

которую удобнее использовать при вычислении дисперсии. Здесь – случайная величина, значения которой равны квадратам значений самой случайной величины X, а соответствующие вероятности - те же самые.

Итак, для определения дисперсии можно использовать следующие формулы:

для ДСВ

(2.5)

или

(2.6)

для НСВ

(2.7)

или

. (2.8)

Дисперсия вычисляет среднее значение квадратов отклонений , т.е. характеризует разброс значений случайной величины вокруг ее среднего значения, но измеряется в квадратных единицах измерения СВ. Использование квадратов в определении дисперсии является вынужденной мерой, т.к. если убрать символ квадрата, то при достаточно больших отклонениях положительные и отрицательные по знаку отклонения могут аннулироваться и среднее отклонение окажется близким к нулю. Чтобы компенсировать эту вынужденную меру, вводят среднее квадратическое отклонение ,которое определяется по формуле:

. (2.9)

Среднее квадратическое отклонение , как и дисперсия , характеризует разброс значений случайной величины вокруг ее среднего значения и измеряется в тех же единицах, в каких измеряется изучаемая случайная величина.

Вопросы для самоконтроля

1. Дайте определение дискретной и непрерывной случайной величины.

2. Какие случайные величины являются непрерывными?

3. Каким условиям должна удовлетворять функция плотности распределения непрерывной случайной величины?

4. Что представляет собой ряд распределения дискретной случайной величины?

5. Перечислите числовые характеристики случайных величин.

6. Для какой характеристики случайной величины используется дисперсия и среднее квадратическое отклонение?

Пример 2.1

Дискретная случайная величина задана законом распределения. Найти числовые характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение. Указать их смысловое значение.

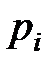
	0,3	0,1	0,2	0,4

Решение:

Проверим, что закон распределения задан правильно:

.

Найдем числовые характеристики.

Математическое ожидание вычислим по формуле (2.1):

.

Используя формулу (2.6), определим дисперсию :

.

Cреднее квадратическое отклонение по формуле (2.9) равно:

.

Итак, среднее значение ДСВ, определяемое . Разброс значений вокруг ее математического ожидания характеризуется и .

Для определения числовых характеристик НСВ в формулах (2.2), (2.7), (2.8) используется функция плотности распределения , которая задает закон распределения НСВ. Эти законы могут быть весьма разнообразными, но на практике в большинстве случаев встречаются законы определенных типов. Важнейшим из них является нормальный закон распределения, которому подчиняется большинство НСВ.

Не нашли, что искали? Воспользуйтесь поиском: