Краткие теоретические сведения. Получив случайную выборку, и изучив ее, мы должны сделать выводы о числовых параметрах распределения г.с

Получив случайную выборку, и изучив ее, мы должны сделать выводы о числовых параметрах распределения г.с. или определить закон распределения, т.е. его параметры. Найти точные значения указанных параметров нет возможности, следовательно, необходимо найти подходящие статистические оценки этих величин, т.е. такие выборочные характеристики, которые бы позволили получить по возможности более точные их значения. Для этого необходимо по имеющейся выборке провести первичную обработку собранных статистических данных. Значения, которые принял в результате исследования или наблюдения интересующий нас признак называют вариантами. Первичную обработку статистических данных проводят с помощью рабочих таблиц. Для заполнения таблицы необходимо расположить варианты в возрастающем или убывающем порядке. Эту операцию называют ранжированием.

Вариационным рядом называется ранжированный ряд вариантов с соответствующими частотами , причем – есть объем выборки. В зависимости от объема выборки и от того, какие значения может принимать признак, вариационные ряды делятся на дискретные и непрерывные (интервальные).

Вариационный ряд называется дискретным, если значения признака отличаются друг от друга на некоторую величину, и непрерывным, если значения признака могут отличаться на сколь угодно малую величину.

В случае, если изучаемый показатель принимает немного различных числовых значений, в частности для выборок малого ( 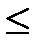30) объема строят дискретный вариационный ряд (таблицу). В первом столбце которой, перечисляют все значения признака (статистики) в возрастающем порядке, во втором соответствующие частоты . Если все значения признака встречаются по одному разу, т.е. все , то второй столбец можно опустить. Далее заполняют таблицу, в зависимости от того, какие формулы будут применяться для нахождения выборочных характеристик, а именно:

Выборочная средняя.

Характеризует центр выборочного распределения и находится по формулам:

, (5.1)

где - число различных значений.

Если ввести понятие и обозначение относительной частоты

, (5.2)

то формула примет вид:

. (5.3)

Выборочная дисперсия.

Выборочная дисперсия показывает абсолютный разброс и вычисляется для выборок большого объема по одной из формул:

, (5.4)

, (5.5)

, (5.6)

. (5.7)

Выборочное исправленное стандартное отклонение в квадрате

Для выборок малого объема применяется эта выборочная статистика, которая тоже характеризует абсолютный разброс и , поэтому вычисляется по формуле:

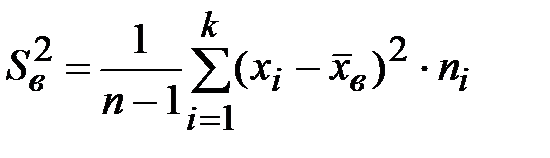. (5.8)

Выборочное стандартное отклонение.

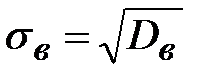. (5.9)

Выборочное исправленное стандартное отклонение.

. (5.10)

Интервальный (непрерывный) вариационный ряд строят для непрерывно варьирующего признака, а также для выборок большого объема ( >30), где в первом столбце таблицы записывают непересекающиеся интервалы. Во втором столбце таблицы записывают количество значений, попавших в каждый интервал. Далее осуществляют переход от интервального ряда к дискретному, заменяя интервалы их серединами 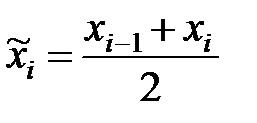и записывают эти значения в следующем столбце таблицы.

Для вычисления выборочных характеристик применяют формулы указанные выше, в которых 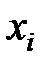заменяют на .

Например, формула (5.1) для выборочной средней будет иметь вид:

, (5.11)

а формула (5.4) для выборочной дисперсии:

. (5.12)

Все описанные выше выборочные характеристики носят названия точечных оценок, поскольку определяются одним числом (точкой).

Для оценки относительного разброса значений относительно среднего значения используют коэффициент вариации 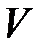, который измеряется в % и для выборок большого и малого объемов находится по формулам соответственно:

. (5.13)

. (5.14)

Точечная оценка параметра генеральной совокупности, особенно при вы­борке малого объема, может существенно отличаться от оцениваемого параметра и приводить к грубым ошибкам. По этой причине используют интервальные оценки.

Интервальная оценка неизвестного параметра распределения представляет собой доверительный интервал, в который с заданной надежностью (доверительной вероятностью) попадает оцениваемый параметр.

Границы доверительного интервала вычисляются по выборке.

Доверительный интервал для оценки генеральной средней или, что одно и тоже, параметра а нормального распределения имеет вид:

-∆ < a < +∆, (5.15)

где - среднее выборочное, а ∆ - точность оценки.

Точность оценки ∆ находится следующим образом:

а) для малых выборок ( 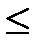30)

, (5.16)

где Т (n, γ) - коэффициент доверия, значения которого для выборки объема n и заданной надежности 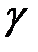находятся по таблице (приложение 3).

б) для больших выборок ( >30)

, (5.17)

- коэффициент, значения которого для заданной надежности 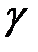находятся по таблице значений функции Лапласа (приложение 2), а именно: является решением уравнения

Графическое изображение вариационных рядов.

Для изображения дискретных вариационных рядов служит полигон. Для его построения в прямоугольной системе координат наносят точки с координатам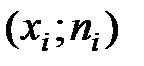и или , которые соединяют отрезками прямых. Полученная ломаная линия называется соответственно полигон частот или полигон относительных частот.

Гистограмма служит для изображения интервального вариационного ряда. Для ее построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, соответствующие интервалам варьирования, и на них, как на основаниях, строят прямоугольники с высотами равными или частотам 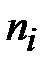, или относительным частотам , или плотностям относительных частот ( –длина интервала). Полученная фигура, состоящая из примыкающих друг к другу прямоугольников, называется соответственно: или гистограммой частот или гистограммой относительных частот или гистограммой плотностей относительных частот.

Замечание. При построении полигона или гистограммы можно выбирать разный масштаб на осях координат.

Средние величины и их применение к оценке качества

В статистических исследованиях активно используется средняя величина, которая представляет собой обобщенную характеристику и применяется для сравнения различных совокупностей по некоторому количественному признаку, что позволяет делать из этого сравнения необходимые выводы. Различают несколько видов средних величин: среднюю арифметическую, среднюю геометрическую, среднюю гармоническую, среднюю квадратическую и др. Исчисляются как простые, так и взвешенные средние. Вид каждой средней отличается особыми свойствами, поэтому при ее выборе в каждом конкретном случае необходимо принимать во внимание характер статистических данных и задачи, поставленные в связи с расчетом средней величины. Чаще всего используют арифметическую средневзвешенную:

(5.18)

где – весовые коэффициенты, причем, как правило, .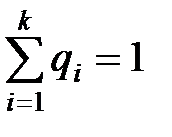

При сравнительном анализе (оценке качества) однотипных объектов вычисляют обобщенную оценку, как некоторую среднюю относительных показателей 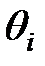. Относительные показатели рассчитываются как отношение единичных к базовым показателям.

Например, для расчета обобщенной по всем турам оценки работников, можно использовать формулу:

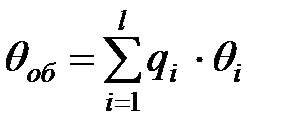, (5.19)

где – число туров, 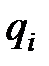– весовые коэффициенты для каждого тура, а 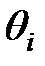– относительные показатели, рассчитываемые для каждого 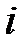– го тура как отношение среднего числа баллов к максимальному в 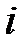– ом туре.

Для определения индивидуальной средневзвешенной оценки конкретного работника в формуле (5.19) относительные показатели 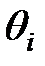для каждого тура определяются как отношение числа набранных баллов данного работника к максимальному числу баллов.

Вопросы для самоконтроля

1. Какой ряд наблюдений называют вариационным рядом?

2. Чем отличаются дискретные и интервальные вариационные ряды и методы их обработки?

3. Как графически можно представить дискретный вариационный ряд?

4. Для чего служит гистограмма и как ее построить?

5. Перечислите основные числовые характеристики вариационного ряда.

6. Какие формулы используют для расчета средней арифметической?

7. Какие числовые характеристики используют для оценки разброса значений изучаемого признака около средней?

8. Какие величины называются модой и медианой?

9. Что означает доверительная вероятность?

10. Как определяется интервальная оценка генеральной средней?

11. Как заданная точность влияет на величину доверительного интервала?

Пример 5.1

Аттестация работников предприятия проводилась в три этапа. Количество работников, проходивших аттестацию равно =48. Оценки экспертами выставлялись в баллах. Распределение количества баллов первого тура, из максимальных 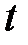=23 по всем участникам, приведено в таблице.

Необходимо:

1) Провести первичную обработку результатов, а именно: построить гистограмму частот; определить среднее количество баллов в первом туре по всем участникам; оценить их абсолютный и относительный разброс.

2) Полагая, что количество баллов есть случайная величина, имеющая нормальное распределение, найти доверительный интервал, в котором с вероятностью 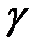=0,9524 заключено среднее количество баллов.

3) В результате обработки данных второго тура, в котором максимально можно было набрать 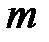=17 баллов, среднее число баллов по всем участникам составило =10,11. Для третьего тура с максимумом 12 баллов, среднее число получилось равным =5,21. Определить средневзвешенную по трем турам оценку для всех участников, учитывая, что весовые коэффициенты для каждого из трех туров соответственно равны: =0,45, =0,30, 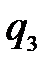=0,25.

4) Работник набрал следующее количество баллов в каждом туре: в первом – 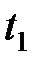=14; во втором – =8; в третьем – =7 баллов. Вычислить индивидуальную средневзвешенную оценку по трем турам для этого работника и сравнить ее со средневзвешенной группы аттестуемых.

Решение:

1) В рассматриваемом примере в аттестации участвовало 48 человек, т.е. объем выборки =48. Вся область наблюдаемых значений (количество набранных баллов) разбита на =6 непересекающихся интервалов. Первая строка частичные интервалы, вторая – частоты из условия задачи.

Построим гистограмму частот (рис. 5.1). Для этого по оси абсцисс отложим интервалы, в которые попадают наблюдаемые значения, а затем на этих интервалах как на основаниях построим прямоугольники, высоты которых равны соответствующим частотам .

Рисунок 5.1.

Для вычисления выборочных характеристик применим формулы (5.11) и (5.12). Результаты вычислений оформим в виде расчетной таблицы. В первом столбце укажем частичные интервалы, во втором – частоты , в третьем столбце запишем середины интервалов.

Интервалы по количеству верных ответов
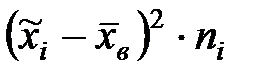
(0;4] (4;8] (8;12] (12;16] (16;20] (20;24]				108,58 247,30 87,85 44,94 155,68 275,33
				919,68

Суммируя результаты четвертого столбца, получим . Разделив эту сумму на объем выборки найдем значение выборочной средней (среднее число баллов): 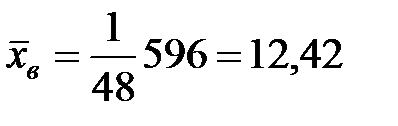. Сумму результатов последнего столбца, разделив на объем выборки, получим по формуле (5.12) значение выборочной дисперсии: . Тогда выборочное стандартное отклонение по формуле (5.9) будет равно: .

Коэффициент вариации определим по формуле (5.13), в результате получим:

2) Судя по гистограмме можно сделать предположение, что количество набираемых участниками баллов, есть случайная величина, имеющая распределение близкое к нормальному. Чтобы найти доверительный интервал, в котором с вероятностью 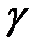=0,9524 заключено среднее число баллов, необходимо определить точность Δ интервальной оценки. Воспользуемся формулой (5.17) для выборок большого объема: где - корень уравнения . При заданной надежности интервальной оценки 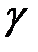= 0,9524 или , получаем, что значение функции Лапласа 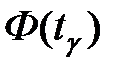= 0,4762, следовательно, ее аргумент по таблице значений функции Лапласа (см. приложе­ние 2) должен быть равен =1,98. Итак, найдено, тогда . Вычислим границы доверительного интервала: 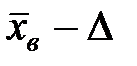=12,42-1,25=11,17; =12,42+1,25=13,67. Доверительный интервал имеет вид: (11,17;13,67). Таким образом, с вероятностью 0,9524 среднее число правильных ответов заключено между 11,17 и 13, 67.

3) Для определения общей по всем турам средневзвешенной оценки работников, участвующих в аттестации, используем формулу (5.19), где =3 туров, весовые коэффициенты =0,45, =0,30, 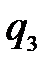=0,25. Вычислим относительные показатели для каждого тура:

; ; .

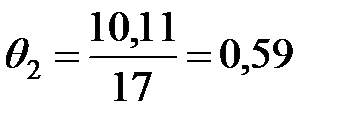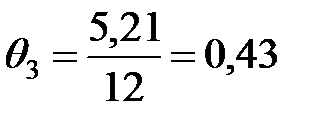Итак,

.

4) Для определения индивидуальной средневзвешенной оценки конкретного работника в формуле (5.19) весовые коэффициенты остаются прежними, а относительные показатели для каждого этапа будут следующими:

; ; .

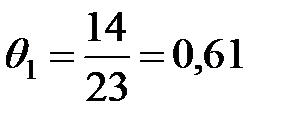Тогда,

.

Итак, индивидуальная средневзвешенная оценка данного работника выше общей средневзвешенной для всей группы атестуемых.

Не нашли, что искали? Воспользуйтесь поиском: