Краткие теоретические сведения. Нормальный закон распределения случайной величины является самым распространенным видом распределения непрерывных случайных величин

Нормальный закон распределения случайной величины является самым распространенным видом распределения непрерывных случайных величин. Нормальному закону подчинены случайные ошибки всевозможных измерений, с ним приходится сталкиваться при анализе и прогнозировании различных явлений в технике, экономике, социологии и других областях знаний.

Говорят, что случайная величина X распределена нормально, если ее функция плотности распределения имеет вид:

(3.1)

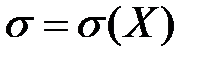где и – параметры распределения, а именно: а = М (Х) - математическое ожидание, или среднее значение, случайной величины X; - её дисперсия; - среднее квадратическое отклонение.

График функции (3.1) называется нормальной кривой (рис. 3.1) и имеет колоколообразный, симметричный относительно прямой вид. Как и для функции плотности любого вида, имеет место равенство: , т.е. площадь, ограниченная нормальной кривой и осью абсцисс равна единице.

Рисунок 3.1

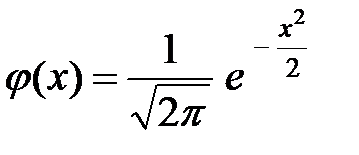. (3.2)

Эта функция называется функцией Гаусса. Таблица значений функции для неотрицательных значений аргумента приведена в таблице (приложение 1). При значения функции принимают =0. Для отрицательных значений аргумента х используют свойство четности: .

Вероятность попадания нормально распределенной случайной величины в интервал (α; β) вычисляется по формуле:

, (3.3)

где - функция Лапласа. Таблица значений функции для неотрицательных значений аргумента приведена в таблице (приложение 2). При значения функции принимают =0,5. Для отрицательных значений аргумента х используют свойство нечетности: .

Вычислим вероятность того, что нормально распределенная СВ отклонится от своего математического ожидания не более чем на .

= .

Поскольку эта вероятность близка к единице, то в статистике принято считать достоверным такое событие. Таким образом, имеет место так называемое правило «трех сигм»: отклонение СВ от ее математического ожидания практически не превышает , т.е. практически достоверно, что все значения СВ, распределенной по нормальному закону принадлежат интервалу .

Вопросы для самоконтроля

1. Какая случайная величина называется величиной, распределенной по нормальному закону?

2. Назовите параметры нормального распределения.

3. Какая формула используется для расчета вероятности попадания нормально распределенной случайной величины в заданный интервал?

4. Сформулируйте правило трех сигм для нормально распределенной случайной величины.

Пример 3.1

Функция плотности распределения вероятностей случайной величины 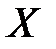имеет вид: 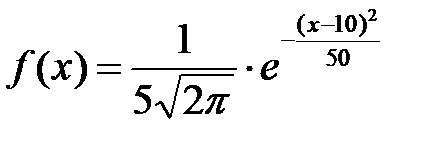. Найти математическое ожидание , среднее квадратическое отклонение , дисперсию случайной величины 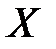и вероятность ее попадания в интервал (4; 15).

Решение:

Поскольку функция плотности задана, то сравнивая ее с общим видом (3.1) нормального закона распределения вероятностей, ясно, что параметрами этого закона являются: а = 10 и σ = 5, следовательно, - математическое ожидание; - среднее квадратическое отклонение; - дисперсия случайной величины .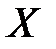

Чтобы найти вероятность попадания случайной величины в интервал (4;15), воспользуемся формулой (3.3) при а = 10, σ = 5, α = 4, β= 15. Получим:

где Ф (1) = 0,3413; Ф (- 1,2) = - Ф (1,2) = - 0,3849 (см. приложение 2).

Окончательно получим:

Р (4< X < 15) = 0,3413 - (- 0,3849)= 0,7262 ≈ 0,73.

Пример 3.2

Предполагается, что вес готового блюда - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием =220 гр. и средним квадратическим отклонением 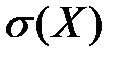=5 гр. Определить вероятность того, что случайно выбранное блюдо будет иметь вес:

a) больше =216 гр.;

b) менее =227 гр.;

c) определить число блюд из =11, отобранных для контрольного взвешивания, у которых вес будет не менее =212 и не более =230 гр.

Решение:

По условию случайная величина 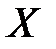– вес блюда имеет нормальное распределение с параметрами =220 и =5.

a) вероятность того, что случайно выбранное блюдо будет иметь вес больше 216 гр., можно рассматривать как вероятность того, что его вес заключен в интервале от 216 до .

Замечание. Учитывая правило трех сигм, можно заменить на величину =220+3 5=235.

Используя формулу (3.3), получим:

= 0,4987+0,3849=0,8836.

b) вероятность того, что случайно выбранное блюдо весит менее 227 гр.– это, то же самое, что вероятность того, что его вес окажется в интервале от 0 до 227. Следовательно, по формуле (3.3), будем иметь:

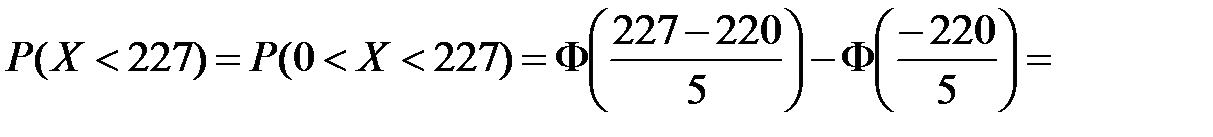
= 0,4192–(–0,5)=0,5+0,2486=0,7486,

поскольку (при значения =0,5).

c) Для определения числа блюд, которые будут иметь вес не менее 212 и не более 230 гр. из 14 взвешенных, сначала найдем вероятность того, что случайно выбранное блюдо будет иметь вес в этих пределах:

= 0,4772–(–0,4452)=0,4772+0,4452=0,9224.

Следовательно, 92,24% блюд от общего их числа имеют указанный вес. Из 11 блюд этот процент составит: 0,9224 11=10,15 10 (блюд).

Не нашли, что искали? Воспользуйтесь поиском: