Частотные характеристики типовых звеньев.

К простейшим типовым звеньям относятся:

· усилительное,

· инерционное (апериодическое 1-го порядка),

· интегрирующие (реальное и идеальное),

· дифференцирующие (реальное и идеальное),

· апериодическое 2-го порядка,

· колебательное,

· запаздывающее.

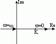
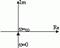
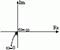
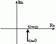
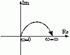
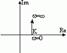
Частотная передаточная функция	Амплитудная и фазовая характеристики	Амплитудно-фазовая частотная характеристика

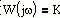
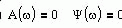
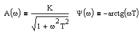
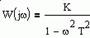
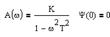
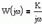
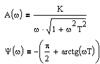
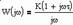
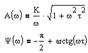
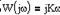
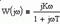
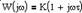
Частотные характеристики звена определяют его реакцию на гармонический входной сигнал в установившемся режиме (т.е. после завершения переходных процессов). Частотной характеристикой динамического звена называют функцию комплексного аргумента jw, полученную путем формальной замены s на jw в выражении передаточной функции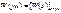

Получим связь частотной характеристики с известными понятиями. Для этого рассмотрим динамическое звено с передаточной функцией W(s) и сигналами, 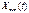. Пусть,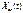 – абсолютно интегрируемые функции и равны нулю при t<0. Тогда частотные спектры этих сигналов (преобразование Фурье) этих функций можно определить следующим образом – .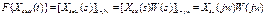

Получим отношение спектров -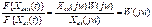

Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала.

Знание частотной характеристики звена позволяет определить выходной спектр по входному

.

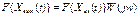Рассмотрим динамическое звено –

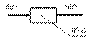
Получим спектр выходного сигнала – импульсной характеристики 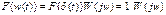Тогда имеем , то есть преобразование Фурье от импульсной характеристики равно частотной характеристике динамического звена.

Рассмотрим передаточную функцию, состоящую из n-го количества элементов.

Последовательность выражений позволяет найти амплитуду и фазу колебаний на выходе системы при гармоническом воздействии на ее входе.

Модуль этого выражения показывает, во сколько раз увеличивается или уменьшается амплитуда колебаний на выходе системы по сравнению с амплитудой колебаний на входе.

Аргумент вектора F(jω) описывает фазовый угол колебаний по отношению колебаниям на входе => (*) определяет частотную характеристику, называемую амплитудно-фазовой частотной характеристикой (АФЧХ).

АФЧХ строится на комплексной плоскости 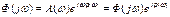j – мнимая единица.

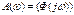- коэффициент, характеризующий изменение амплитуды при изменении частоты, при изменяющейся частоте, называется амплитудно-частотной характеристикой (АЧХ).

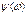дает представление о фазовом сдвиге выходных колебаний и он называется фазово-частотной характеристикой (ФЧХ)

АФЧХ:

Вещественные или мнимые частотные характеристики связаны с АЧХ и ФЧХ следующим образом:

При анализе САР на устойчивость и качества процесса регулирования, а также при решении других задач, часто обращаются к ЛЧХ

Усиление L(ω) = 20lg|Ф(jω)| = 20lgA(ω) [дБ] – является единицей логарифмической относительно величины. Изменения относительно двух величин в 10 раз соответствует изменению усиления на 20 дБ.

Известно, что АЧХ представляет собой отношение 2-х амплитуд: входного и выходного сигналов.

Версия по Петрову:

К простейшим типовым звеньям относятся:

· усилительное,

· инерционное (апериодическое 1-го порядка),

· интегрирующие (реальное и идеальное),

· дифференцирующие (реальное и идеальное),

· апериодическое 2-го порядка,

· колебательное,

· запаздывающее.

Частотные характеристики усилительного звена можно получить по его передаточной функции, при этом АФХ, АЧХ и ФЧХ определяются следующими соотношениями:

.

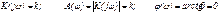Частотные характеристики интегрирующего звена определяются соотношениями:

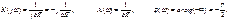
Не нашли, что искали? Воспользуйтесь поиском: