
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Исследование устойчивости линеаризованной системы
Главное требование к системе управления − обеспечение ее устойчивости. Схема объекта, приведенная на рисунке 15, является линейной нестационарной (передаточные функции W1(s), W2(s), W3(s) зависят от коэффициента K, т.е. изменяются с течением времени). Необходимо провести анализ устойчивости системы при различных значениях коэффициента K или определить такие значения K, при которых линеаризованная система устойчива, что позволит судить об устойчивости системы с нелинейным объектом.
Объект имеет три входа: два управления (u1 и ũ2) и возмущение (Mтр). Система будет устойчивой в том случае, когда выполняются условия устойчивости по каждому из входов, поэтому необходимо рассмотреть три случая с одним из входных воздействий, когда два других равны нулю или их нет.
Предположим, что входом является момент Mтр, u1 = 0 и u2 = 0. Тогда структурную схему линеаризованного объекта (рисунок 15) можно представить в виде, представленном на рисунке 16, а. Блоки сравнения (вычитания) заменены коэффициентами передачи (−1). Далее осуществляются эквивалентные структурные преобразования, показанные на рисунках 16, б, в.
Рисунок 16 – Эквивалентные преобразования структурной схемы системы
Для преобразованной схемы запишем передаточную функцию объекта:

| (46) |
С учетом обозначений передаточных функций (42) – (45) выражение (46) представим в виде:

| (47) |
В результате элементарных преобразований получим:

| (48) |
В рассматриваемом случае система по входу Mтр разомкнутая, поэтому динамика будет определяться характеристическим полиномом:

| (49) |
Выполним обратную подстановку передаточных функций (42) – (45) в выражение (49) и запишем полином в виде:

| (50) |
Раскрывая скобки и выполняя группировку слагаемых, получим:

| (51) |
Введем следующие обозначения:

| (52) |

| (53) |

| (54) |

| (55) |
и запишем характеристическое уравнение в виде:

| (56) |
Для исследования устойчивости системы необходимо определить корни λ1, λ 2 и λ 3 уравнения (56), их действительные и мнимые части как функции от коэффициента K. Из условия устойчивости

| (57) |
определяется допустимый диапазон изменения K.
Можно применить средства пакета Matlab для определения корней уравнения (56) при различных значениях коэффициента K, изменяющегося в определенных пределах. С учетом формулы (40) можно допустить, что K изменяется от −2 Iн до 2 Iн, а для вычисления корней уравнения (56) можно применить команду Matlab вида
lambda = roots ([a3 a2 a1 a0])
По корням характеристического уравнения можно оценить не только устойчивость, но и качество (быстроту затухания переходных процессов). Степени устойчивости η и колебательности μ можно определить по соответствующим формулам:

| (58) |

| (59) |
Листинг программы m-файла построения зависимости степени устойчивости и колебательности от тока 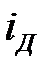 :
:
Un=1500; %V
Pn=586*10^3; %W
Wn=600*2*pi/60; %rad/sec
KPD=0.94;
Ry=0.056; %Om
Rv=0.048; %Om
p=6;
In=Pn/Un/KPD
Imax=1.2*In
cE=(Un-In*(Ry+Rv))/In/Wn
cM=Pn/(Wn*In^2)
L=2*Un/(5*p*Wn*In)
J=(6*L*Pn^2)/(Ry^2*Wn^2*In^2)
Mn=Pn/Wn
beta=0.004*Mn
R1=2*Rv+Ry
R2=Ry
T1=3*L/(2*Rv+Ry)
T2=L/Ry
In=415.6;
K=-2*In:100:2*In
a3=R1*R2*T1*T2*J
a2=R1*R2*(T1*T2*beta+T1*J+T2*J)
i=1
while(i<18)
a1(i)=R1*R2*(T1*beta+T2*beta+J)+K(i)^2*cM*cE*(R1*T1+R2*T2)
a0(i)=R1*R2*beta+K(i)^2*cM*cE*(R1+R2)
lambda=roots([a3 a2 a1(i) a0(i)])
eta(i)=abs(max(real(lambda)))
mu(i)=max(abs(imag(lambda)./real(lambda)))
i=i+1
end
plot(K,eta)
hold on
plot(K,mu)
По результатам вычислений строим зависимости  и
и  от коэффициента
от коэффициента  , а следовательно, и от тока двигателя
, а следовательно, и от тока двигателя 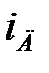 . Графики функций
. Графики функций  и
и  приведены на рисунке 18, из которого видно, что степень устойчивости отрицательна при любых токах, т. е. объект по входному воздействию
приведены на рисунке 18, из которого видно, что степень устойчивости отрицательна при любых токах, т. е. объект по входному воздействию  устойчив. Колебательный характер динамических процессов проявляется только при значительных токах, когда степень устойчивости
устойчив. Колебательный характер динамических процессов проявляется только при значительных токах, когда степень устойчивости  увеличивается и достигает значения 7,1.
увеличивается и достигает значения 7,1.
| η |
| μ |

Рисунок 17 – Графики зависимости степени устойчивости и колебательности от тока iд
| Ω |
| u1 |
а
| Ω |
| u1 |
б
| u1 |
| Ω |
в
Рисунок 18 – Эквивалентные преобразования структурной схемы системы
Запишем передаточную функцию для преобразованной схемы объекта:

| (60) |

| (61) |
С учетом обозначений передаточных функций (42) – (45) выражение (61) представим в виде:

| (62) |
В результате элементарных преобразований получим:

| (63) |
Очевидно, характеристический полином передаточной функции совпадает с характеристическим полиномом передаточной функции системы, когда входным воздействием является момент трения Mтр (49), следовательно динамика системы в обоих случаях одинакова, и графики зависимости степени устойчивости η и колебательности μ от тока двигателя iд в рассматриваемом случае такие же, как на рисунке 17.
Третий случай, при котором входным воздействием является ũ2, рассмотрим при синтезе регулятора, поскольку с определением корней характеристического уравнения связана одна из методик синтеза регулятора.
Не нашли, что искали? Воспользуйтесь поиском: