ЛАБОРАТОРНАЯ РАБОТА № 8. Цель работы:экспериментальное изучение распределения магнитного поля соленоида.

ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА

Цель работы: экспериментальное изучение распределения магнитного поля соленоида.

Приборы и оборудование: лабораторный стенд, имеющий соленоид, датчик индукционный на рейтере, плату объектов; генератор сигналов; осциллограф; прибор для изменения силы тока; набор соединительных проводов.

Введение

Рис. 1.

Магнитное поле соленоида представляет собой результат сложения полей создаваемых круговыми токами, расположенными вплотную и имеющими общую ось. Сечение соленоида схематично показано на рисунке 2.

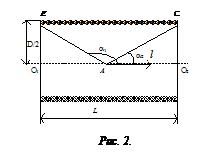Распределение магнитной индукции по длине соленоида вдоль его оси О₁О₂ описывается выражением 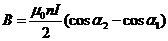(1):

, (1)

где 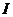– сила тока, протекающего по соленоиду; – магнитная постоянная; – число витков на единице длины; и 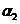– углы между осью соленоида (по направлению вектора ) и прямыми от исследуемой точки А до концов соленоида (точки Е и С соответственно).

Для бесконечно длинного соленоида магнитная индукция 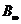вычисляется по формуле:

(2)

Индукция магнитного поля в любой точке на оси соленоида конечной длины всегда меньше индукции магнитного поля бесконечно длинного соленоида в 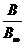раз, или с учетом (1) и (2):

,

откуда

. (3)

Зная геометрические параметры соленоида (длину 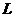и диаметр 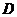), можно рассчитать и 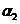, а следовательно, и индукцию магнитного поля для любой точки оси соленоида. Для центра соленоида выражение для индукции имеет наиболее простой вид (в этом случае ).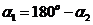

Обозначив 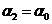, а 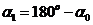и подставив в (3) получим выражение для индукции магнитного поля в центре соленоида, :

,

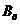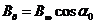из геометрических соображений:

,

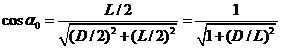тогда

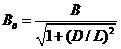
или

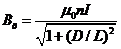. (4)

Постановка задачи

В данной работе для изучения магнитного поля соленоида используется индукционный датчик, который необходимо проградуировать. Для этого необходимо найти зависимость э.д.с. индукционного датчика 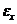от величины индукции магнитного поля . С этой целью индукционный датчик устанавливается в центре соленоида, где неоднородность магнитного поля наименьшая. Меняя ток соленоида 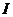(соответственно ), измеряют 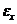. Рассчитав по формуле (4) индукцию магнитного поля в центре соленоида 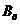, строят градуировочный график зависимости э.д.с. датчика 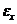от индукции . Из него определяют постоянную индукционного датчика.

Затем установив в соленоиде некоторое значение тока и перемещая индукционный датчик вдоль оси соленоида фиксируют его положение 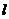на рейторе, измеряют 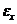(). Далее по градуировочному графику каждому значению 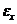ставят в соответствие значение и строят график зависимости (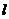). Таким образом получают кривую распределения индукции магнитного поля вдоль оси соленоида.

Не нашли, что искали? Воспользуйтесь поиском: