ЛАБОРАТОРНАЯ РАБОТА № 9. Цель работы: изучение процессов в колебательном контуре, имеющем электроемкость, индуктивность и сопротивление; определение периода

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ В КОНТУРЕ

Цель работы: изучение процессов в колебательном контуре, имеющем электроемкость, индуктивность и сопротивление; определение периода, частоты и логарифмического декремента колебаний.

Приборы и принадлежности: лабораторный стенд, имеющий набор объектов на плате; генератор сигналов ГСФ-1 или ГСЭ-1; осциллограф С1-137 или С1-112А; набор соединительных проводов.

Введение

Причиной возникновения колебаний является чаще всего вывод (отклонение) системы, обладающей инертностью, из положения равновесия и предоставления ее самой себе. Тогда она начнет совершать колебания около положения равновесия. Такие колебания называются собственными (свободными) колебаниями системы.

Вследствие неизбежных потерь энергии колебательного движения (трения в механических системах, нагревания проводника, диэлектрика в конденсаторе, излучение электромагнитных волн в электрических колебательных системах и т.п.), колебания в системе постепенно затухают, и она возвращается в исходное состояние. Поэтому собственные колебания всегда являются затухающими. Затухание напряжения в контуре графически изображено на рисунке 1.

Затухающие колебания не являются периодическими. Условным периодом (чаще говорят просто – периодом) затухающих колебаний называется промежуток времени между двумя последовательными максимальными или минимальными значениями колеблющейся величины. На рисунке 2 представлены затухающие колебания электрического тока и указаны условные периоды затухания.

По своей природе колебания могут быть механическими, электромагнитными, электромеханическими и т.п. Электрические колебания могут возникать в цепи, содержащей индуктивность и емкость. Такую цепь называют колебательным контуром.

Понять процессы, происходящие в колебательном контуре, поможет рисунок 3.

На рисунке 4 изображен колебательный контур с параллельным соединением индуктивности L и емкости С. Сопротивлением R здесь учитывается тот факт, что во всяком реальном контуре есть потери энергии и, простоты ради, будем полагать, что они происходят только в этом сопротивлении. Возбуждение колебаний в данном контуре производится путем подачи на него коротких импульсов напряжения, равных по длительности времени обратного хода луча осциллографа.

За время длительности импульса конденсатор заряжается до напряжения . При разряде конденсатора через и 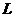в катушке возникает ЭДС самоиндукции . В паузах между импульсами внешнее напряжение к контуру не приложено и по второму правилу Кирхгофа сумма падений напряжений на , , 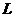должна быть равна нулю:

(1)

Учитывая, что 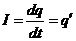, и поделив обе части уравнения на 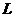, получаем дифференциальное уравнение затухающих колебаний:

. (2)

Решение уравнения (2) при < имеет вид:

, (3)

где – заряд на конденсаторе в момент времени , 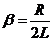– коэффициент затухания, 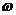– циклическая частота.

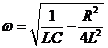. (4)

При малых затуханиях, т.е. при << :

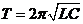. (5)

В соответствии с (3) напряжение на конденсаторе будет изменяться по закону:

. (6)

Энергия, запасенная в контуре за время длительности импульса, постепенно убывает по экспоненциальному закону:

.

Затухание колебаний при этом принято характеризовать логарифмическим декрементом колебаний , равным логарифму отношения амплитуд двух последовательных колебаний (рис. 5, где – амплитуды):

. (7)

		Рис. 5.

При малом затухании:

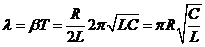. (8)

Часто вместо логарифмического декремента для характеристики контура используют добротность :

. (9)

При больших затуханиях, таких, что >> , вместо колебаний происходит апериодический разряд конденсатора (рис. 6).

Значение сопротивления, при котором колебательный процесс переходит в апериодический, называют критическим сопротивлением контура. Оно определяется из выражения (4) при или :

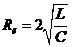. (10)

Постановка задачи

В данной работе изучаются затухающие колебания, возбуждаемые в колебательном контуре, содержащем сопротивление , конденсатор и катушку индуктивности .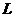

На экране осциллографа получают устойчивую картину затухших колебаний. Затем, используя изображение колебаний на экране, определяют период и частоту колебаний. Логарифмический декремент колебаний определяют по следующей методике.

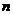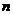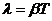Прологарифмируем выражение, описывающее убывание амплитуды колебаний , где – амплитуда после совершения «» полных колебаний. Имеем: , где – количество полных колебаний за время . Согласно формуле (8) . Поэтому:

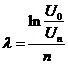. (11)

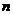Измерив по экрану осциллографа амплитуду , число колебаний и амплитуду после совершения «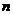» полных колебаний , по формуле (11) рассчитывают логарифмический декремент колебаний.

Не нашли, что искали? Воспользуйтесь поиском: