Теоретическое введение. Емкостью конденсатора называется величина, определяемая отношением заряда на обкладках конденсатора к разности потенциалов (напряжению) между ними.

Емкостью конденсатора называется величина, определяемая отношением заряда на обкладках конденсатора к разности потенциалов (напряжению) между ними.

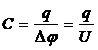(1)

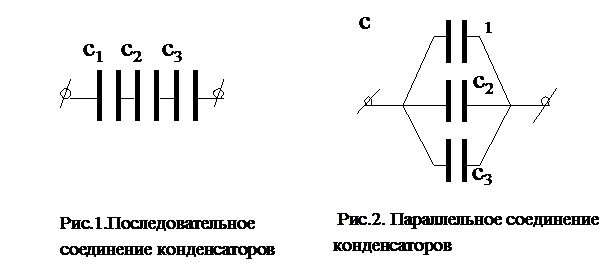
Конденсаторы могут быть соединены в батареи. При последовательном соединении n конденсаторов (см. рис.1) емкость батареи С' определяется из соотношения:

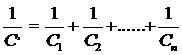(2)

При параллельном соединении (см.рис.2) общая емкость С" равна сумме емкостей конденсаторов

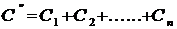(3)

Единицей измерения электроемкости в системе СИ является Фарад (Ф). На практике широко используются:

1 микроФарад ( 1 мкФ=10^-6 Ф) и

1 пикоФарад ( 1 пФ=10^-12 Ф).

Иногда емкость конденсатора может быть рассчитана по формуле. Например, известны формулы для емкости плоского и сферического конденсаторов:

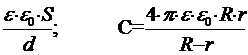С= (4)

Однако чаще емкость конденсатора определяют из электрических измерений. Существует несколько способов измерения емкости. Один из них основан на измерениях, так называемого, емкостного сопротивления конденсатора R_c в цепи переменного тока (см. рис. 3). Из теории переменного тока известно:

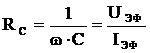, (5)

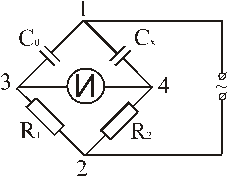где w - циклическая частота тока (w = 2pn), U _эф, I _эф -эффективные значения напряжения и тока.

Используя выражение (5), получим формулу для расчета емкости:

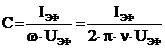(6)

Другой метод измерения емкости основан на сравнении двух емкостей, включенных в схему моста переменного тока. Такая схема показана на рис.4. Здесь С_о - конденсатор с известной емкостью, С_х - конденсатор с искомой емкостью. R₁ , R₂ - омические сопротивления переменной величины, И - индикатор тока. Изменяя соотношение между сопротивлениями R₁ и R₂, можно добиться равенства потенциалов точек 3 и 4, что соответствует условию равновесия моста переменного тока, т.е. j₃=j₄. Это равенство можно преобразовать так:

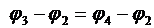(7)

(8)

Пусть в состоянии равновесия по плечам 1-3-2 моста течет ток с эффективным значением I₁, а по плечам 1-4-2 - ток I₂.

Тогда в соответствии с законом Ома для плеч 2-3 и 2-4 можно записать:

,

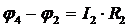
с учетом соотношения (7)

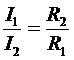(9)

Аналогично:

,

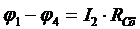
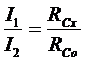
и с учетом уравнения (5)

(10)

Из сравнения (9) и (10) вытекает

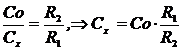(11)

Таким образом, неизвестная емкость легко может быть найдена по эталонной емкости и отношению сопротивлений.

Не нашли, что искали? Воспользуйтесь поиском: