ПОСЛЕДОВАТЕЛЬНАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА СО СМЕШАННОЙ НАГРУЗКОЙ.

Рассмотрим участок цепи, состоящий из последовательно соединенных активного сопротивления, конденсатора емкостью С и катушки с индуктивностью L (рис.139), по которому течет ток .

В случае квазистационарного тока, согласно закону сохранения энергии, общее мгновенное напряжение на этом участке будет складываться из мгновенных напряжений на каждом из последовательно включенных элементов:

.

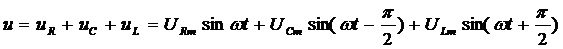Так как складываемые напряжения представляют собой гармонические колебания одной частоты, то и мгновенное напряжение также будет изменяться с такой же частотой.

Рассчитать амплитудное значение этого напряжения и сдвиг фаз по отношению к силе тока можно двумя способами: используя тригонометрические формулы для суммы и разности или методом векторных диаграмм (рис.140). Воспользуемся методом векторных диаграмм.

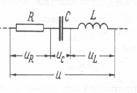
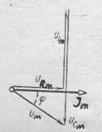
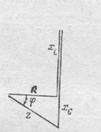
РИС.139 РИС.140 РИС.141 РИС.142 РИС.143

Построив вектор-амплитуду результирующего напряжения как векторную сумму амплитуд напряжений на всех элементах, получим: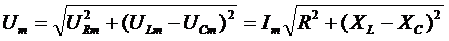

Следовательно, и в случае смешанного последовательного соединения различных нагрузок, амплитудные значения силы тока и общего напряжения связывает соотношение аналогичное закону Ома: , где 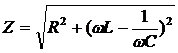представляет собой полное сопротивление (импеданс) данного участка цепи.

Как видно из рис.140, суммарное мгновенное напряжение сдвинуто по фазе относительно силы тока и изменяется соответственно по закону . Сдвиг фаз можно определить с помощью векторной диаграммы:

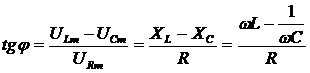. Из этой формулы следует, что в зависимости от соотношения индуктивного и емкостного сопротивлений участка цепи общее мгновенное напряжение может как опережать, так и отставать по фазе от мгновенной силы тока.

Важно отметить, что, хотя мгновенные значения напряжений складываются, полное сопротивление цепи не является арифметической суммой активного, емкостного и индуктивного сопротивлений.

Разность индуктивного и емкостного сопротивлений называется реактивным сопротивлением цепи: .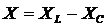

Эта величина может быть положительной или отрицательной, что по физическому смыслу будет определять опережение или отставание по фазе напряжение от силы тока в цепи. Следствием последовательного соединения элементов цепи и векторной диаграммы напряжений является «треугольник» сопротивлений.

Полное сопротивление в этом прямоугольном треугольнике представляет собой гипотенузу, а катеты – это активное и реактивное сопротивления.

На рис. 141 треугольник сопротивлений в цепи с положительным реактивным сопротивлением. На рис.142 и рис.143 показаны векторная диаграмма и треугольник сопротивления для цепи «емкостного» характера, т.е. реактивное сопротивление в этом случае отрицательно.

На рис.144 представлен один из многочисленных вариантов общего случая последовательного соединения различных элементов.

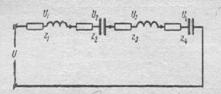
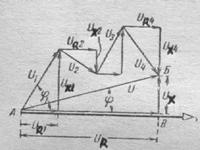
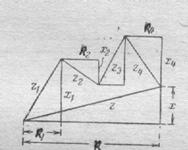
РИС.144 РИС.145 РИС.146

На рис.145 показано построение векторной диаграммы напряжений для данной цепи, которая позволяет рассчитать амплитуду общего напряжения цепи и сдвиг фаз между током и напряжением 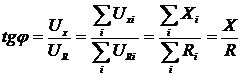. На рис. 146 представлено построение общего треугольника сопротивлений, который позволяет рассчитать общий импеданс цепи и также сдвиг фаз между током и напряжением: .

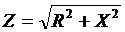Активное сопротивление всей цепи R является арифметической суммой активных сопротивлений на всех участках, а реактивное сопротивление всей цепи X – алгебраическая сумма всех реактивных сопротивлений.

Не нашли, что искали? Воспользуйтесь поиском: