РАЗВЕТВЛЕННАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА. МЕТОД ПРОВОДИМОСТЕЙ.

На практике часто используются разветвленные цепи, в которых необходимо рассчитать токи во всех ветвях и ток всей цепи, а также активную, реактивную и полную мощность цепи.

ЦЕПЬ ИЗ ДВУХ ПАРАЛЛЕЛЬНЫХ ВЕТВЕЙ.

Рассмотрим простейшую цепь переменного тока, состоящую из двух параллельных ветвей с последовательно включенными активными сопротивлениями и катушками индуктивности и подключенную к источнику синусоидального напряжения 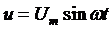(рис.151). В соответствии с законом сохранения заряда сила мгновенного тока в неразветвленной части цепи будет равна сумме токов в параллельных ветвях .

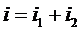В каждой ветви ток будет отставать от напряжения на ветви (см. § 52), а напряжение на ветвях общее. Поэтому построим векторную диаграмму токов, считая, что мгновенные значения токов в первой и второй ветвях отстают от напряжения соответственно на 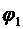и 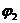(рис.152).

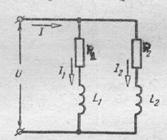
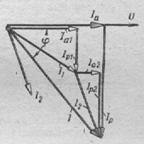
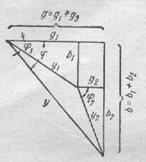
РИС.151 РИС.152 РИС.153 РИС.154

Амплитудные и действующие значения силы токов в ветвях можно найти, используя следующие соотношения:

, , , , .

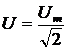Используя векторную диаграмму и эти соотношения, можно найти действующее значение силы тока и сдвиг фаз между током и напряжением:

,

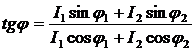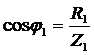, где и .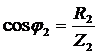

Соответственно можно рассчитать активные, реактивные и полные мощности ветвей: , , ,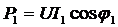

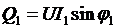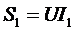, , , а также активную, реактивную и полную мощность всей цепи:

, , .

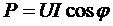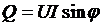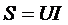Если в одной из ветвей будет включена емкостная нагрузка, то вектор силы тока в этой ветви будет опережать вектор напряжения на некоторый угол, а величина суммарного тока и сдвиг фаз будут определяться соотношением реактивных сопротивлений ветвей.

МЕТОД ПРОВОДИМОСТЕЙ.

Если в цепи больше двух параллельных ветвей, то для рационального расчета используется метод проводимостей, который основан на следующем.

1)Ток в каждой цепи является векторной суммой активной и реактивной составляющих (рис.153). Например, для рассмотренной выше цепи действующие значения токов в ветвях можно рассчитать по следующим формулам: ,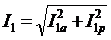

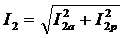
2)Активные составляющие совпадают по фазе с напряжением и равны: , ,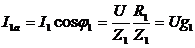

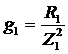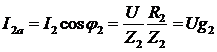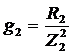, , где g₁ и g₂- активные проводимости первой и второй ветвей.

3) Реактивные составляющие токов отличаются по фазе от напряжения на 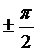и рассчитываются по формулам:

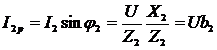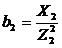, , , , где b₁ и b₂ – реактивные проводимости первой и второй ветвей.

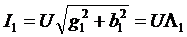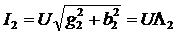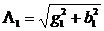Тогда: , , где и 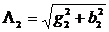- полные проводимости обоих ветвей.

Проводимость всей цепи может быть рассчитана по формуле:

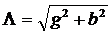, где g=g₁+g₂ и b=b₁+b₂ и представлена треугольником проводимостей (рис.154), который является следствием векторной диаграммы токов.

4)Общая сила тока в цепи может быть рассчитана как модуль векторной суммы активной и реактивной составляющих 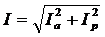, где и .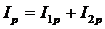

5)Сдвиг фаз между током и напряжением: 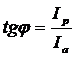или .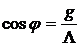

6)Активную, реактивную и полную мощность цепи можно рассчитать по формулам: , , ,

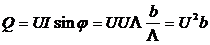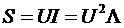В общем случае разветвленной цепи применяют метод эквивалентных (равнозначных) схем, т.е. цепь последовательно упрощают, заменяя сопротивление разветвленных участков эквивалентными сопротивлениями. Для этого рассчитывают активные и реактивные проводимости параллельных ветвей, а затем полную проводимость и сопротивление разветвленного участка. В результате разветвленная цепь заменяется неразветвленной – эквивалентной. Затем рассчитывается ток, сдвиг фаз между током и напряжением, активная, реактивная и полная мощность цепи.

Не нашли, что искали? Воспользуйтесь поиском: