ВЫНУЖДЕННЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. РЕЗОНАНС НАПРЯЖЕНИЙ.

Как уже обсуждалось в § 50, рассмотренная цепь из последовательно соединенных индуктивности, емкости и активного сопротивления может рассматриваться как колебательная система, так как в ней возможно возникновение электромагнитных колебаний с собственной частотой

при .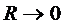

Эти колебания являются затухающими, так как энергия, сосредоточенная в контуре в момент возникновения колебаний выделяется в виде тепла на активном сопротивлении во время колебательного процесса.

Тогда, при включении в контур источника переменной ЭДС, его можно рассматривать как элемент, инициирующий в контуре вынужденные колебания с частотой . Следовательно, уравнение

представляет собой уравнение вынужденных электромагнитных колебаний под действием внешней периодически изменяющейся ЭДС.

Используя введенные в § 50 физические величины: собственную частоту и коэффициент затухания это уравнение можно представить и в виде .

Как известно, для вынужденных колебаний характерно явление резонанса, которое заключается в возрастании амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к резонансной частоте, зависящей от параметров колебательной системы.

В рассматриваемой цепи - колебательном контуре вынужденные колебания совершают сила тока, заряд и напряжение на конденсаторе, а также напряжение на катушке индуктивности.

Резонансными кривыми называются зависимости амплитудных значений, совершающих вынужденные колебания физических величин, от частоты внешнего воздействия, т.е., в нашем случае, от частоты источника ЭДС.

Закон Ома для рассматриваемой цепи – колебательного контура позволяет проанализировать зависимость амплитуды силы тока от частоты источника ЭДС: .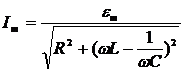

Если амплитудное значение ЭДС, а также величины активного сопротивления, емкости и индуктивности постоянны, то амплитудное значение силы тока зависит только от частоты.

Максимальная амплитуда силы тока: при . В этом случае частота источника ЭДС совпадает с собственной частотой колебательного контура: ,

т.е. для вынужденных колебаний силы тока наблюдается резонанс.

На рис.155 показаны резонансные кривые для амплитуды силы тока в зависимости от частоты источника при различном активном сопротивлении колебательного контура. Резонанс выражен тем отчетливее, чем меньше активное сопротивление, т.е. чем меньше коэффициент затухания .

Колебания заряда и напряжения на конденсаторе совпадают по фазе. Найдем зависимость амплитуды колебаний заряда от частоты. Как показано в § 51 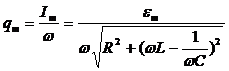. Если использовать выражения для собственной частоты и коэффициента затухания, то это выражение преобразуется к виду:

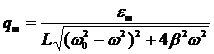. Максимальное значение амплитуды заряда достигается при минимальном значении подкоренного выражения. Возьмем производную от подкоренного выражения по частоте и приравняем ее нулю: или . Подставив это значение в выражение для амплитудного значения заряда, получим: .

Так как , то максимальная амплитуда напряжения на конденсаторе достигается при том же значении частоты источника ЭДС: .

На рис.156 и рис.157 показаны резонансные кривые для амплитудных значений заряда и напряжения на конденсаторе при различных активных сопротивлениях контура.

Резонансная частота для заряда и напряжения всегда меньше, чем резонансная частота для тока, а резонанс выражен тем больше, чем меньше активное сопротивление контура.

РИС.155 РИС.156 РИС.157 РИС.158

Максимальное значение напряжения на катушке индуктивности (см.§ 51) преобразуем также, используя понятия собственной частоты и коэффициента затухания:

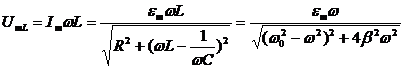. Резонансную частоту можно найти, взяв производную по частоте от этого выражения и приравняв ее к нулю. Резонансная частота для напряжения на катушке индуктивности равна: .

Если преобразовать и сравнить выражения для резонансных частот на конденсаторе и на катушке индуктивности с резонансной частотой тока: , , , то можно сделать вывод, что, общем случае, резонансная частота для напряжения на конденсаторе всегда меньше, а для напряжения на катушке индуктивности всегда больше, чем резонансная частота для силы тока (и напряжения на активном сопротивлении). Резонансные кривые для напряжений на активном сопротивлении, катушке индуктивности и емкости показаны на рис.158.

Для представляющих практический интерес контуров с малым затуханием, 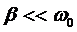, членом 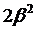можно пренебречь. В этом случае резонанс для всех переменных электрических величин: силы тока, заряда и напряжения на конденсаторе, напряжения на катушке индуктивности наступает практически одновременно при частоте источника, равной частоте свободных колебаний в контуре:

. При резонансе сдвиг фаз между током и напряжением равен нулю (рис.159).

Для контуров с большим затуханием, если активное сопротивление так велико, что , подкоренное выражение становится мнимым и резонансная кривая не имеет максимума, т.е. резонанс отсутствует. В этом случае, зависимость, например, напряжения на конденсаторе от частоты источника представлена на рис.157 для сопротивления R₃.

Рассмотренное явление резонанса при последовательном соединении источника с элементами контура называется резонансом напряжений. При этом - называется волновым или характеристическим сопротивлением, а максимальные напряжения на катушке индуктивности и конденсаторе равны и противоположны по фазе.

Для контуров с малым затуханием характерен «острый» резонанс и высокая добротность , которая (см.§ 50) характеризует относительную убыль энергии контура за период при свободных колебаниях.

Физический смысл добротности для контуров с малым затуханием при резонансе.

1)Добротность показывает во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней ЭДС (рис.158). .

Следовательно, необходимо учитывать, что при резонансе, даже при небольшой внешней ЭДС, напряжения на индуктивности и емкости могут достигать большой величины, опасной для жизни человека:

2)Можно показать, что добротность характеризует относительную ширину резонансной кривой: . Шириной резонансной кривой, или полосой пропускания называется интервал частот , ограниченный частотам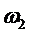и и , на которых амплитуда в меньше амплитуды при резонансе (рис.160).

Следовательно, добротность – величина обратная относительной ширине пропускания или относительной ширине резонансной кривой.

Резонанс используется для выделения из сложного «сигнала» (зарегистрированного напряжения) нужной составляющей. Это имеет практическое значение в радиотехнике при приеме и настойке на определенную частоту радиосигнала. Чем выше добротность контура, тем уже резонансная кривая и тем легче «отстраиваться» от передач, ведущихся на соседних частотах.

На практике добротность контура подбирается и с учетов необходимого качества приема сигнала, так как с уменьшение ширины резонансной кривой уменьшается информация (диапазон частот) «пропускаемый» контуром.

РИС.159 РИС.160 РИС.161

РЕЗОНАНС ТОКОВ.

Рассмотрим простейшую цепь переменного тока из двух параллельных ветвей, как систему, в которой возникают вынужденные электромагнитные колебания под действием источника внешнего напряжения (рис.161).

Рассчитать силу тока и сдвиг фаз между током в цепи и напряжением источника можно по формулам: , ,

, , .

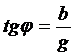Анализ этих формул показывает, что так как активная и реактивная проводимости зависят от частоты, то и сила тока во всей цепи также зависит от частоты. при b=0. Найдем частоту, при которой амплитуда тока минимальна:

, .

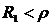Это выражение имеет действительное значение при: 1) и или 2) и 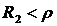. Если , то амплитуда силы тока минимальна при .

В этом случае активные и реактивные проводимости равны, сдвиг фаз между током и напряжением равен нулю (рис.162). Кроме того равны активные и реактивные составляющие токов и токи в ветвях (рис.163). Поэтому это соотношение параметров в ветвях цепи называют «резонанс токов».

РИС.162 РИС.163 РИС.164 РИС.165

При резонансе токов суммарная реактивная мощность цепи равна нулю: , реактивные мощности и . В этом случае цепь обладает только активным сопротивлением и в цепи выделяется только активная мощность.

Резонанс токов возникает и в цепи, содержащей несколько ветвей с активным сопротивлением, емкостями и индуктивностями при том же условии – реактивная проводимость всей цепи равна 0.

ТРЕХФАЗНЫЙ ТОК.

Переменный ток, рассмотренный ранее, называется однофазным. Трехфазным называется ток, представляющий собой совокупность трех однофазных токов, сдвинутых друг относительно друга по фазе.

Простейший генератор трехфазного тока отличается от генератора однофазного тока тем, что имеет три обмотки. При вращении либо этих обмоток в поле постоянного магнита (рис.164), либо самого магнита (рис.165) в обмотках возникают переменные ЭДС одинаковой частоты, сдвинутые друг относительно друга по фазе так, что сумма трех фазных углов составляет .

Если амплитуды ЭДС равны, а сдвиг фаз между двумя любыми смежными ЭДС равен , то трехфазная система называется симметричной. В этом случае на обмотках возникают

одинаковые по величине, но сдвинутые по фазе напряжения: , , .

Использование несвязанных между собой обмоток эквивалентно трем отдельным генераторам и требует для передачи электроэнергии потребителю три пары проводов.

Соединение обмоток между собой позволяет уменьшить количество проводов при передаче энергии и поэтому широко используется в технике.

При соединении обмоток звездой (рис.166) они имеют одну общую точку. Напряжение на каждой обмотке называется фазным. Проводник, соединенный с точкой общего потенциала, называется нулевым проводом. Проводники, соединенные со свободными концами обмоток, называются фазными проводами.

Фазные напряжения, в этом случае, это напряжения между фазными проводами и нулевым проводом. Напряжение между фазными проводами называется линейным. Ток, текущий через обмотки, называется фазным током, а ток текущий в линии, - током линии.

Из векторной диаграммы, при соединении звездой, следует, что . Кроме того при этом фазные токи равны токам в линии.

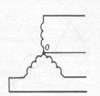
РИС.166 РИС.167 РИС.168 РИС.169 РИС.170

Если каждую обмотку замкнуть на одинаковую нагрузку R, то суммарная сила тока по нулевому проводу , так как из векторной диаграммы .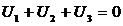

Соединение обмоток генератора звездой позволяет использовать при передаче энергии четыре провода вместо шести.

При соединении обмоток треугольником (рис.168) они образуют замкнутый контур с весьма малым сопротивлением. Линейный провод отходит от общих точек начала одной фазы и конца другой и, поэтому фазные напряжения равны линейным (рис.169).

Из векторной диаграммы токов (рис.170) следует, что

,

На практике используется не только соединение обмоток генератора, но и соединение между собой нагрузок звездой или треугольником. Таких комбинаций возможного соединения генератора и нагрузок – четыре.

РИС.171 РИС.172 РИС.173 РИС.174

При соединении звезда – звезда (рис.171) на всех нагрузках разное напряжение, но если сопротивление нагрузок приблизительно равно, то ток по нулевому проводу практически равен нулю.

Тем не менее, нулевой провод нельзя убирать или ставить в него предохранители потому, что без него на каждую из пар нагрузок действует линейное напряжение, причем оно распределяется в соответствии с сопротивлением нагрузок. Получается, что напряжение, подаваемое на нагрузку, зависит от ее сопротивления, что неэффективно и опасно.

Если генератор и нагрузки соединены звезда – треугольник (рис.172), то на каждой нагрузке, независимо от ее сопротивления, одинаковое напряжение, равное линейному.

При соединении треугольник – треугольник (рис.173) на всех нагрузках фазное напряжение, независимо от их сопротивления.

Если генератор и нагрузки соединены треугольник – звезда (рис.174), то на каждой нагрузке напряжение равно .

Трехфазный ток используется для получения вращающегося магнитного поля. В этом случае трехфазный ток подводится к трем обмоткам, расположенным на неподвижной станине – статоре. Внутри статора помещен стальной барабан – ротор, вдоль образующих которого в пазах уложены провода, соединенные между собой на обоих торцах кольцами.

Обмотки статора создают магнитный поток одинаковой величины, но сдвинутый по фазе, т.е. он как бы вращается относительно ротора. В обмотках ротора возникают индукционные потоки, которые, в свою очередь, взаимодействуют с вращающимся магнитным потоком, что приводит ротор во вращение, т.е. получается электродвигатель достаточно простого устройства.

При увеличении скорости ротора уменьшается относительная скорость движения его проводников относительно магнитного поля. Если бы он достиг той же скорости вращения, что и магнитный поток статора, то индукционный ток равнялся бы нулю и, соответственно, вращающий момент стал бы равным нулю.

Следовательно, при наличии тормозного момента магнитный поток и ротор не могут вращаться с той же скоростью, что и поток статора (синхронно), - скорость вращения ротора всегда несколько меньше. Поэтому двигатели такого типа называются асихронными (несинхронными).

Трехфазная система, изобретенная русским инженером М.О.Доливо-Добровольским в XIX, применяется во всем мире для передачи и распределения энергии. Доливо-Добровольский первым получил вращающееся магнитное поле с помощью трехфазного тока и построил первый асинхронный двигатель. Трехфазная система обеспечивает наиболее экономичную передачу энергии и позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы.

На практике, например, электрические лампы изготавливаются на номинальные напряжения 127 и 220В. Способ их включения в цепь трехфазного тока зависит от величины линейного напряжения трехфазной сети.

Лампы с номинальным напряжением 127 В включаются звездой с нейтральным проводом при линейном напряжении сети 220 В или треугольником при линейном напряжении сети 127 В.

Лампы с номинальным напряжением 220 В соответственно включаются звездой в сеть с линейным напряжением 380 В и треугольником в сеть с напряжением 220 В.

Обмотки трехфазных двигателей изготавливаются на номинальные фазные напряжения 127, 220 и 380 В. Каждый трехфазный двигатель может быть включен или звездой в трехфазную сеть с линейным напряжением, превышающим его фазное в раз, или треугольником, если линейное напряжение сети равно фазному напряжению его обмотки. Обычно на паспорте двигателя указано, например: треугольник -220В, звезда – 380В.

ТЕМА X. МАГНЕТИКИ

Не нашли, что искали? Воспользуйтесь поиском: