Методы измерения сопротивлений

Цель – познакомиться с различными методами измерения сопротивлений.

Приборы и принадлежности: амперметр и вольтметр постоянного тока, источник постоянного тока, реохорд, магазин сопротивлений, гальванометр, проводники, ключ, измеритель сопротивления М 416, измеряемые сопротивления.

Измерение сопротивлений методом амперметра и вольтметра.

Метод основан на использовании закона Ома для участка цепи

(2.8)

Этот способ может быть применён для измерения различных по величине сопротивлений. Достоинством этого метода является возможность пропускать по измеряемому сопротивлению такой же ток, как и в условиях его работы, что важно при измерении сопротивлений.

Измерения можно производить по двум схемам, показанным на рис. 2.5

R_A R_x

A

R_V

V

схема 1

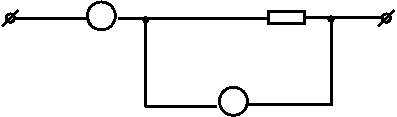R_A R_x

А

R_V схема 2

V

Рис.2.5. Два способа включения вольтметра

В схеме 1 вольтметр показывает напряжение на последовательно соединённых резисторе и амперметре. Поэтому напряжение на сопротивлении будет

U_R = U – IR_A, U, I, R_A – соответственно показания вольтметра, амперметра и сопротивление амперметра.

Из закона Ома найдём

(2.9)

В схеме 2 амперметр измеряет не только ток I_R, проходящий через измеряемое сопротивление, но ток I_V, проходящий через вольтметр. Поэтому ток, идущий через резистор, связан с током, идущим через амперметр, соотношением

(2.10)

где R_V – сопротивление вольтметра.

Из (2.8) и (2.10) найдём

R = . (2.11)

Выбор схемы измерения

В практике измерений сопротивлений этим методом подсчет сопротивления часто производят по приближённой формуле

, (2.12)

где R^| – приближенное значение измеряемого сопротивления.

Считая амперметр и вольтметр идеальными, то есть R_A→ 0, R_V → ∞. В этом случае нужно знать, какую схему следует выбирать для того, чтобы величина погрешности была невелика. Оценим выражения погрешностей для обеих схем.

Систематическая относительная погрешность схемы 1

(2.13)

Не нашли, что искали? Воспользуйтесь поиском: