СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ

Газовые смеси подчиняются закону Дальтона, согласно которо­му давление Р_см смеси идеальных газов равно сумме парциальных давлений Р_i.

Парциальным давлением называется давление, создаваемое от­дельным компонентом в полном объеме при температуре смеси. Если объем смеси V_см давление Р_см, то парциальное давление от­дельного компонента

. (2.8)

где V_i - приведенный объем отдельного компонента при парамет­рах смеси.

Состав смеси может быть задан одним из следующих способов.

I Массовый состав смеси:

а) в абсолютных единицах массы

, (2.9)

где G₁,G₂,G₃ и т.д, - массы отдельных компонентов смеси;

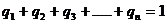или

. (2.10)

где q_i - массовая доля отдельного компонента смеси.

2.Объемный состав смеси:

а) в абсолютных единицах объема

, (2.11)

где V₁,V₂,V₃ и т.д - приведенные объемы отдельных компонентов смеси, м³;

б) в относительных долях (объёмных)

или , (2.12)

где r_i - объемная доля отдельного компонента .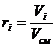

Смесь может быть задана числом молей М как сумма чисел молей n отдельных компонентов. Мольная доля отдельного компо­нента равна объемной доле:n_i = r_i,

Кажущаяся молекулярная масса смеси

, (2.13)

где m_i- молекулярная масса отдельных компонентов смеси.

Газовая постоянная смеси

. (2.14)

Соотношение между массовыми и объемными долями

. (2.15)

ЗАДАЧИ

2.1 Процентный массовый состав дымового газа следующий: = 15 %, = 6 %; = 79 %. Найти молекулярный вес газа, газовую постоянную, плотность и удельный объем при нормальных условиях. Найти парциальное давление каждого газа, входящего в смесь, считая давление смеси р = 740 мм рт.ст.

Ответ: m_см= 29,8;v_см = 0.751 м³/кг; r = 1,33 кг/м³;

= 9997,5 Па

2.2 Найти давление смеси по манометру, если масса ее М = 20 кг; V = 4 м³; t = 100 °С, причем состав смеси по объему = 0,4; = 0,6.

Ответ: 0,297 Мпа.

2.3 Анализом определен объемный состав газовой смеси: =0,12; =0,05; = 0,03; = 0,80. Определить плотность и удельный объем смеси при нормальных условиях, молеку­лярный вес, газовую постоянную и относительный массовый состав ее.

Ответ: m_см = 29,8; v_см = 0.752 м³/кг; r_см = 1,33 кг/м³; = 0.177 и т.д.

2.4 Смесь состоит из 50 кг дымовых газов, массовый состав которых: СО₂₌ 14 %; О₂ = 6 %; Н₂О = 5 %; N₂ = 75 % и 75 кг воздуха. Определить массовый и объемный составы смеси, если массо­вый состав воздуха: О₂ = 23,2 %; N₂ = 76,8 %.

Ответ: = 0,761 и т.д.; = 0,78 и т.д.

2.5 Состав горючего газа по массе: Н₂ = 1,5 %; СО = 28 %;СО₂ = 10,0 %; N₂ = 60,5 %. Определить объемный состав, плотность и удельный объем при Р = 0,2 МПа и t = 100 ^oС, а также количест­во киломолей в 1 т смеси. Ответ: = 0,525 и т.д.;

v_см = 0.655 м³/кг;r_см = 1,53 кг/м³; К_см= 41,4 кмоля.

2.6 До какого давления по манометру нужно довести смесь газов, состоящую из = 0,14; = 0,25 и = 0,61, чтобы парциальное давление в ней составляло = 0,12 МПа? Какое дав­ление при этом будет иметь СО? Принять В = 780 мм рт. ст.

Ответ: 0,73 МПа, 0,513 МПа.

2.7. Для светильного газа анализ дал следующий состав в объемных долях: 50 % Н₂; 30 % СН₄; 15 % СО; 3 % CO_2; 2 % N₂. Чему равны газовая постоянная и средний молекулярный вес этого газа? Каков состав в весовых долях и чему равна плотность газа при 25^оС и давлении 750 мм рт.ст. Ответ: R_см= 0,698 кДж/кг К; r_см = 0,461 кг/м³.

2.8 Определить объем 3 кг смеси, относительный массовый состав которой следующий: = 0,4; =0,2; = 0,4. Температура смеси t = 50^oС, давление по манометру Р = 600 мм рт.ст. Давление атмосферы нормальное.

Ответ: V = 2,38 м³.

2.9 Определить массу 4 м³ смеси, относительный объемный состав которой следующий: 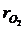= 0,4; = 0,2; = 0,4. Температура смеси t = 50 ^oС; давление по манометру Р = 0,04 МПа В = 700 мм рт. ст. (93,325 кПа). Ответ: 7,07 кг.

2.10 Дымовые газы поступают в первый ход котла при t₁ = 1200 ^oС, а выходят при t₂ = 800 ^oС. Состав газов по объему: = 12 %; 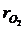= 5 %; = 8 %, остальное азот. Вычислить ко­личество теплоты, теряемое 1 м³ (при нормальных условиях) газовой смеси, считая зависимость нелинейной.

Ответ: 160 ккал/м³ (670,4 кДж/м³),

ТЕПЛОЕМКОСТЬ ГАЗОВ

Теплоемкостью называют количество тепла, которое необходимо сообщить телу (газу), чтобы повысить температуру какой-либо коли­чественной единицы его на I ^ОC.

В зависимости от выбранной количественной единицы различают весовую теплоемкость (С - кДж/кг К), объемную теплоемкость ( - кДж/нм³ К) и мольную теплоемкость (mС - кДж/моль К).

Для определения значений этих теплоемкостей достаточно знать значение одной какой-либо из них. Удобнее всего иметь значение мольной теплоемкости.

Весовая теплоемкость тогда определяется из выражения

, кДж/кг К, (3.1)

а объемная теплоемкость получается равной

, кД./нм³К. (3.2)

Объемная и весовая теплоемкости связаны между собой следую­щей зависимостью.

. кДж/нм³ К, (3.3)

где r - плотность газа при нормальных условиях.

Теплоемкость газа зависит от его температуры. По этому приз­наку различают среднюю и истинную теплоемкость.

Если q - количество тепла, сообщаемое единице количества газа (или отнимаемое от него) при изменении температуры газа от t₁ до t₂ (или, что то же, от T₁ до Т₂), то величина

, (3.4)

представляет собой среднюю теплоемкость в пределах от t₁ до t₂.Предел этого отношения, когда разность температур стремится к нулю, называется истинной теплоемкостью. Аналитически последняя определяется как,

.

Теплоемкость идеальных газов зависит не только от их темпе­ратуры, но и от их атомности и характера процесса. Теплоемкость реальных газов зависит от их природных свойств, характера процес­са, температуры и давления.

Для газов особо важное значение имеют следующие два случая нагрева (охлаждения):

1) изменение состояния при постоянном объеме;

2) изменение состояния при постоянном давлении;

Обоим этим случаям соответствуют различные значения теплоемкостей.

Таким образом, различают истинную и среднюю теплоемкость:

а) весовую - при постоянном объеме ( и 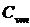) и постоян­ном давлении (С_р и С_pm);

б) объемную - при постоянном объеме ( и ) и постоянном давлении ( и );

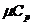в) мольную - при постоянном объеме ( и ) и постоянном давлении ( и ).

Между мольными теплоемкостями при постоянном давлении и при постоянном объеме существует зависимость:

. (3.5)

Отношение теплоемкостей , обозначаемое буквой К, называется показателем адиабаты:

. (3.6)

Этот показатель играет в термодинамике большую роль. Показатель адиабаты зави­сит от атомности газа. Для одноатомных газов К = 1,6, двух­атомных - К = 1,4, трехатомных - К = 1,3.

ЗАДАЧИ

3.1 Определить значение объемной теплоемкости кислорода при постоянном объеме и постоянном давлении, при t = 200 ^oС.

3.2. Определить значение весовой теплоемкости кислорода при постоянном объеме и постоянном давлении при t = 500 ^oС.

Ответ: С_p = 0,92 кДж/кг К; С_v= 0,6536 кДж/кг К.

3.3 Определить среднюю весовую теплоемкость углекислого газа при постоянном давлении в пределах от 0 до 825 ^oС, считая зависимость от температуры криволинейной.

Ответ: С_рm = 1,1 кДж/кг К.

3.4 Вычислить среднюю теплоемкость C_pm для воздуха при постоянном давлении в пределах от 200 до 800 ^oС, считая зависи­мость теплоемкости от температуры криволинейной.

Ответ; С_vm = 1,09 кДж/кг К,

3.5 Найти среднюю теплоемкость C_pm и углекислого газа в пределах от 400 до 1000 ^oС, считая зависимость теплоем­кости от температуры криволинейной.

Ответ: C_pm = 1,24 кДж/кг К;

= 2,4 кДж/нм³ К.

3.6 Определить среднюю весовую теплоемкость при постоян­ном объеме для азота в пределах от 200 до 800 ^oС, считая зави­симость теплоемкости от температуры криволинейной.

Ответ: С_vm= 0,82 кДж/кг К.

3.7 Найти количество тепла, необходимое для нагрева 1 нм³ воздуха от 400 до 1000 ^oС при Р = const, считая зависимость теплоемкости от температуры криволинейной.

Ответ: q_р = 878,6 кДж/нм³.

3.8 В закрытом сосуде объемом V = 300 л находится воз­дух при давлении Р₁ = 3 ата и температуре t₁ = 20 ^oС.

Какое количество тепла необходимо подвести для того, чтобы температура воздуха поднялась до t₂ = 120 ^oС? Задачу решить, принимая теплоемкость воздуха постоянной.

Ответ: Q_v= 76 кДж.

3.9 Найти количество тепла, необходимое для нагрева 1 нм³ смеси газов от 200 до 1200 ^oС при Р = const, если состав сме­си по объему следующий: СО₂ = 14,5 %; 0₂ = 6,5 %; N₂= 79,0 %. Ответ: q_p = 558 кДж/нм³.

3.10 В калориметре с идеальной тепловой изоляцией находит­ся вода в количестве G_в = 0,8 кг при температуре = 15 ^oС. Калориметр изготовлен из серебра, теплоемкость которого С_c = 0,24 кДж/кг К.

Вес калориметра G_к = 0,25 кг, В калориметр опускают 200 г алюминия при температуре t_к= 100 ^oС. В результате этого темпе­ратура воды повышается до 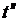= 19,24 ^oС.Определить теплоемкость алюминия. Ответ: С_a = 0,9 кДж/кг К.

4 ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

Первый закон термодинамики является частным случаем закона сохранения и превращения энергии.

Для конечных тепловых процессов, в которых рабочее тело не изменяет своей внешней кинетической энергии, уравнение 1-го за­кона термодинамики для 1 кг газа имеет вид в системе СИ

(4.1)

где q - теплота процесса, Дж/кг;

DU - изменение внутренней энергии, Дж/кг;

l- работа расширения, Дж/кг.

В технической термодинамике учитывают только внутреннюю кинети­ческую энергию газа, зависящую от скорости движения его частиц и их массы, и внутреннюю потенциальную энергию, зависящую от сил взаимодействия атомов и молекул и их взаимного расположения.

Нужно усвоить, что внутренняя энергия есть однозначная фун­кция термодинамического состояния рабочего тела, и поэтому изме­нение внутренней энергии не зависит от характера протекания про­цесса, а зависит только от начального и конечного состояния ра­бочего тела.

Изменение внутренней энергии идеального газа зависит только от температуры и для 1 кг газа определяется по формуле:

(4.2)

Работа расширения l - есть функция процесса: графически в ко­ординатах P-V она изображается площадью под кривой процесса, ограниченной осью абсцисс и ординатами, опущенными на эту ось из точек, характеризующих начало и конец процесса. Математическое выражение работы расширения имеет вид , из которого получаются необходимые формулы для каждого конкретного процесса.

ЗАДАЧИ

4.1 В цилиндре диаметром 0,2 м под поршнем находится газ. При сообщении теплоты поршень приподнялся на 0,4 м. Масса груза с поршнем составляет 200 кг. Определить работу, совершенную газом, количество подведенной теплоты и изменение внутренней энер­гии газа, если = 1,4.

Ответ: L = 80 кгм = 0,785 кДж;

= 0,468 ккал = 1,96 кДж;

Q = 0,655 ккал = 2,745 кДж.

4.2 В процессе расширения 1 кг кислорода подводится 200 кДж теплоты. Какую работу совершит при этом газ, если в резуль­тате процесса температура его понизится на 95^oС. Зависимость теплоемкости от температуры не учитывать (C_v = 0,654 кДж/кг К).

Ответ: 262 кДж/кг.

4.3 Определить изменение температуры 10 кг нефтяного масла при его нагревании и перемешивании, если известно, что количество подводимой теплоты Q = 200 кДж и работа перемешивания L = 36 кДж. Теплоемкость масла 2 кДж/ кг К.

Ответ: = 11,6 ^оС.

4.4 Сколько килограммов свинца можно нагреть от температу­ры 15^оС до температуры его плавления t_пл = 327 ^оС посредст­вом удара молота массой 200 кг при падении его с высоты 2 м? Предполагается, что вся энергия падения молота превращается в теплоту, целиком поглощаемую свинцом. Теплоемкость свинца С_р = 0,1256 кДж/кг К.

Ответ: 0,0969 кг.

4.5 Свинцовый шар падает с высоты 80 м на твердую повер­хность. При этом кинетическая энергия шара переходит в теплоту, 80 % которой им усваивается. На сколько градусов нагревается при падении шар? Теплоемкость свинца С_р = 0,1256 кДж/кг К.

Ответ: на 5 К.

4.6 Испытание двигателя ведется при помощи присоединенного к нему генератора. Напряжение на клеммах генератора постоянного тока U = 220 В, сила тока I = 50 А, к.п.д. генератора z = 0,98. Определить мощность двигателя на валу.

Ответ: N = 11,2 кВт.

4.7. Газ, состояние которого определяется на Р,v- диаграмме рисунок 4.1 точкой I, переводится в состояние 2 по пути 1 с 2. При этом к газу подводится 80 кДж энергии в виде теплоты и от газа получается 30 кДж работы. Затем этот же газ возвращается в исходное состояние в процессе, который описывается кривой 2а1. Сколько энергии в виде теплоты нужно подвести в некотором другом процессе 1d2, чтобы от газа получить 10 кДж работы? Сколько нуж­но подвести или отвести теплоты в процессе 2а1, если на сжатие расходуется 50 кДж энергии в форме работы? Ответ: = 60 кДж; 100 кДж.

Рисунок 4.1 - Изменение состояния газа в процессах

4.8 Состояние газа под поршнем в цилиндре определяется точкой 1 рисунок 4.2. Газ переводится в состояние 2 один раз по пути 1а2 и второй - по пути 1в2. Определить, будут ли отличаться в этих процессах количества отведенной и подведенной теплоты, и если да, то насколько. Извест­но, что давления в точках 1 и 2 равны 0,1 и 0,5 МПа соответствен­но, а изменение объема V₂-V₁ = 0,5 м³.

Ответ: 200 кДж

P

а 2

1 b

v₁ v_{2 V}

Рисунок 4.2 - Изменение состояния газа в процессах

4.9 Определить к.п.д. двигателя автомобиля мощностью 44,0 кВт при расходе топлива 7,4 кг/ч.

Теплоту сгораемого топлива принять равной 40 МДж/кг.

Ответ: z = 0,538.

4.10 Мощность электростанции на выходных шинах составляет 12 мВт. Какое количество топлива В, кг/ч сжигается в топках котлов электростанции, если все потери энергии на станции составляют 70 %, а теплота сгорания топлива Q_H= 30 МДж/кг.

Ответ: В = 4800 кг/ч.

4.11 Определить суточный расход топлива на электростанции мощностью N = 100 мВт, если ее к.п.д.z_ст= 0,35, а теплота сго­рания топлива 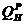= 30 МДж/кг.

Определить также удельный расход топлива на 1 мДж выработан­ной энергии.

Ответ: В сут. = 823 т/сут.;В = 0,0953 кг/МДж.

4.12 На электростанции мощностью N = 100 мВт сжигается топливо с теплотой сгорания 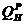= 30 МДж/кг. Коэффициент полез­ного действия станции z_ст = 33,0 %.

Определить часовой расход топлива В. Ответ: В = 36,4 т/ч.

4.13 Паровая турбина расходует 0,00110 кг пара на получе­ние 1 кДж электроэнергии. На производство 1 кг пара необходимых параметров затрачивается 3300 кДж.

Определить к.п.д. паротурбинной установки. Ответ: z = 27,6 %.

4.14. Газ, имеющий массу G = 1 кг, находится под поршнем цилиндра в состоянии 1 рисунок 4.3 с параметрами Р₁= 0,5 МПа и

v₁ = 0,100 м³/кг. Он может перейти в состояние 2 с параметрами Р₂ = 0,1 МПа и v₂ = 0,262 м³/кг посредством процесса 1а2 и 162. Процесс 1а2 протекает без теплообмена, его уравнение Р = . Процесс 1б2 характерен тем, что при его осуществлении теплота сна­чала подводится к газу, а затем отводится от него. В процессе 1б2 давление зависит от объема линейно. Определить работу, которую совершает газ, если происходит процесс 1а2. Какое количество теплоты, подведенное к газу в процессе 1б2 или отведенное, больше по своему абсолютному значению и насколько?

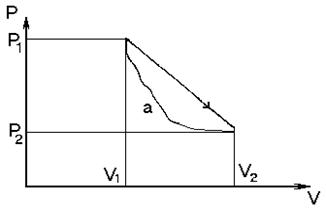
Рисунок 4.3 – Изменение состояния газа в процессах

Ответ: = 35,7 кДж/кг; 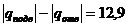кДж/кг.

4.15 Свинцовый шар падает с высоты h = 100 м на твердую поверхность. В результате падения кинетическая энергия шара пол­ностью превращается в тепло. Одна треть образовавшегося тепла пе­редается окружающей среде, а две трети расходуются на нагревание шара. Теплоемкость свинца С_v = 0,1257 кДж/кг К. Определить по­вышение температуры шара.

Ответ: DT = 5,2 К.

4.16 Предполагая, что все потери водяной турбины превраща­ются в тепло и тратятся на нагревание воды, определить к.п.д. турбины по следующим данным: высота падения воды равна 400 м, нагревание воды 0,2 ^oС.

Ответ: z = 78,6 %.

4.17 В машине вследствие плохой смазки происходит нагрева­ние 200 кг стали на 40 ^oС в течение 20 мин.

Определить вызванную этим потерю мощности машины. Теплоем­кость стали принять равной 0,4609 кДж/кг К.

Ответ: 4,18 л.с.

4.18 Найти изменение внутренней энергии 1 кг воздуха при переходе от начального состояния его t₁ = 300 ^oС в конечное при t₂ = 50 ^oС. Зависимость теплоемкости от температуры принять прямолинейной.

Ответ: DU= 185,4 кДж/кг.

4.19 Найти изменение внутренней энергии 2 м³ воздуха, ес­ли температура его понижается от t₁ = 250 ^oС до t₂ = 50 ^oС. Зависимость теплоемкости от температуры принять прямолинейной. Начальное давление воздуха Р₁ = 6 ата.

Ответ: DU= 1042,89 кДж.

4.20 К газу, заключенному в цилиндре с подвижным поршнем, подводится извне 20 ккал тепла. Величина произведенной работы при этом составляет 10000 кгм.

Определить изменение внутренней энергии газа, если количест­во его равно 0,8 кг.

Ответ: DU = -17,43 кДж/кг.

Не нашли, что искали? Воспользуйтесь поиском: