
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПОЛИТРОПНЫЕ ПРОЦЕССЫ
Политропными процессами называются процессы, подчиняющиеся уравнению вида 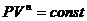 , где n - показатель политропы, принимающий значения от
, где n - показатель политропы, принимающий значения от 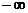 до
до 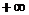 .
.
Изобарный, изотермический, изохорный и адиабатный процессы являются частными случаями политропных процессов.
Показатель политропы этих процессов принимает следующие значения:
а) изобарный процесс n=0, уравнение процесса 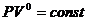 ;
;
б) изотермический процесс 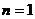 , уравнение процесса
, уравнение процесса  ;
;
в) адиабатный процесс n = К, уравнение процесса 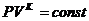 ;
;
г) изохорный процесс  , уравнение процесс
, уравнение процесс 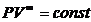 Формулы расчета термодинамических процессов приведены в таблице 5.1.
Формулы расчета термодинамических процессов приведены в таблице 5.1.
ЗАДАЧИ
5.1 Воздух охлаждается от 800 до 100 oС в процессе Р = const Считая зависимость  нелинейной, подсчитать отдаваемое им количество теплоты на 1 м3.
нелинейной, подсчитать отдаваемое им количество теплоты на 1 м3.
Ответ: 976,3 кДж/м3.
5.2 В процессе Р = const к газу теплота подводится так, что температура газа поднимается от t1 100 oС до t2 700 oС. Найти количество подведенной теплоты, изменение внутренней энергии и работу, если Р = 0,2 МПа, а V1 = 3 м3. Задачу решить, определяя количество газа один раз по массе, а другой раз по объему. Теплоемкость принять переменной, считая зависимость С = f(t) линейной.
Ответ: q = 3490 кДж; DU= 2547,5 кДж; l = 945 кДж; V2 = 7,82 м3.
5.3 2 кг воздуха, начальные параметры которого Р1 = 10 ат и t1 = 400 oС, расширяются до тех пор, пока объем не увеличится в 3 раза. Определить начальные и конечные параметры, количество теплоты в процессе, изменение внутренней энергии и работу, если расширение происходит: I) изотермически; 2) по адиабате; 3) по политропе n = 1,2;
4) по политропе n = 1,6 (Сv= 0,722 нДж/кг).
Ответ: 1) l = 427 кДж; P2 = 0,3 МПа;
2) Р2 = 0,21 МПа; Т2= 432 К; l = 344 кДж; DU= 344 кДж;
3)Р2 = 0,262 МПа; Т2=538 К; l = 390 кДж; DU= -194,9 кДж; q=195кДж;
4)P2 = 1,72 ат; Т2= 346 К; l = 314кДж;DU= -473кДк; q = -159кДк.
5.4 В цилиндре воздух сжимается по адиабате так, что объем уменьшается в 5 раз. Начальное давление Р1= 1 ат; начальная температура t1=90 oC. Определить конечную температуру и давление воздуха.
Ответ: 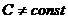 (нелинейная зависимость);
(нелинейная зависимость);
Т2 = 675 К; Р2 = 0,9 МПа.
5.5 В цилиндре дизеля происходит сжатие воздуха по адиабате. Определить конечные давление и температуру, если объем уменьшается в 15 раз. Принять Р1 = 1 ат и t1 = 90 oС.
Ответ: 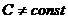 (нелинейная зависимость); Т2= 993 К; Р2 = 41 МПа.
(нелинейная зависимость); Т2= 993 К; Р2 = 41 МПа.
5.6 В цилиндре сжимают воздух так, чтобы его конечная температура была выше температуры воспламенения топлива, равной 750 oС. Сжатие происходит по адиабате. Начальное давление Р1=1 ат. Начальная температура t1=90 oС. Определить минимальное конечное давление и степень сжатия.
Ответ: 3,7 МПа; 13,4 (С =const); 4,5 МПа; 16,3 (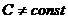 ).
).
Таблица 5.1 – Формулы для расчёта термодинамических процессов
| Процесс | Соотношение между параметрами | Работа, Дж/кг | Теплота, Дж/кг теплоёмкость, Дж/кг | Изменение энтропии Дж/(кг К) |
Изохорический
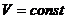
| 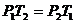
| 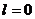
| 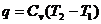 ; ; 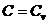
| 
|
Изобарический
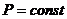
| 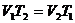
| 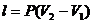
|  ; ;
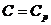
| 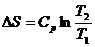
|
Изотермический
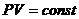
| 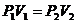
| 
| 
| 
|
Адиабатический
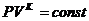
| 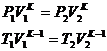
| 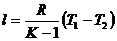
| 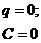
| 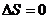
|
Политропический
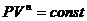
| 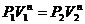
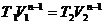
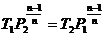
| 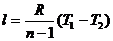
|

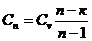
| 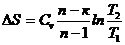
|
5.7 Политропный процесс расширения идет с показателями n = 0,8;
n = 1,2; n = 1,6.
Исследовать процессы и показать относительное расположение политроп в T,s - диаграмме.
5.8 Воздух при нормальных условиях сжимают по адиабате до давления Р2 = 0,3 МПа и затем охлаждают при постоянном давлении до t3= 0 oС. Какую работу нужно совершить для получения 1 м3 воздуха при конечных параметрах (к = const)?
Ответ:370 кДж.
5.9 В цилиндре объемом V = 0,01 м3, закрытом поршнем, находится воздух при Р1 = 1,0 МПа и Т1 = 298 К. Воздух может расширяться до 0,1 МПа;
а) изотермически; б) адиабатически; в) политропно n = 1,3. Определить конечный объем, температуру и совершаемую газом работу. Как велика в случаях "а" и "б" подводимая теплота?
Ответ: а)Т1 = Т2; l = 198 кДж/кг;
б) Т2 = 154 К; l = 107 кДж/кг; в) Т2 = 175 К; l = 118 кДж/кг.
5.10 Компрессорная установка должна ежечасно производить 1000 м3 сжатого воздуха при давлении 1,5 МПа, сжимая его от Р1 = 0,1 МПа и t1 = 20 oС. Какая мощность в кВт потребуется компрессору, если считать, что потери в нём отсутствуют и если сжатие будет производиться: а) изотермически; б) адиабатно; в) политропно с n = 1,3? Сколько теплоты должно отводиться в случаях "а" и "в"? Процессы представить в T,s - диаграмме.
5.11 Во сколько раз изменится абсолютное значение работы адиабатного сжатия 1 кг идеального газа, для которого к = 1,4, начальная температура Т1 и давление Р1 = 0,1 МПа, если конечное давление Р2 в первом процессе равно 1 МПа, а в других увеличивается в 10, 100, 1000 раз?
Как изменится значение работы, если начальная абсолютная температура газа увеличится в 10 раз?
Ответ: 1) соответственно в 2,93; 6,67 и 13,87 раза; 2) при увеличении Т1 в 10 раз во столько же раз возрастет значение работы.
5.12 При адиабатном расширении I кг воздуха (к = 1,40 = const) температура его падает на 120 К.
Какова полученная в процессе расширения работа и сколько теплоты следовало бы подвести к воздуху, чтобы ту же работу получить в изотермическом процессе?
Ответ:  кДж/кг.
кДж/кг.
5.13 Какова начальная температура азота, если конечная температура после совершения процесса адиабатного сжатия t2 = 750 oС. Известна степень сжатия 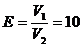 .
.
Теплоемкости считать постоянными.
Ответ: t1 = 135 oС.
5.14 Азот из баллона емкостью 0,05 м3 выпускается в атмосферу настолько быстро, что теплообмен между ней и азотом в баллоне не успевает совершаться. До выпуска давление в баллоне было Р1 = 1,2 МПа и температура t1 = 27,0 oС. После закрытия вентиля температура в баллоне стала t2 = 0,0 oС.
Какова масса выпущенного азота и каким стало давление в баллоне после впуска?
Ответ: DG = 1,413 кг; Р2 = 8,63 МПа.
5.15 В баллоне объемом 40 л находится сжатый кислород при Р1 = 14,0 МПа и при температуре среды. После быстрого открытия выпускного вентиля кислород вытекает в атмосферу; затем вентиль снова закрывается. Теплообмен между содержимым баллона и средой за время выпуска практически не успевает совершаться. Давление в баллоне Р2 после впуска пара оказывается 7,0 МПа. Через некоторое время температура кислорода снова становится равной температуре среды t1 = 20 oС.
Какой стала температура кислорода в баллоне сразу после выпуска? Какое количество кислорода вытекало из баллона? Чему стало равным давление после восстановления первоначальной температуры? Какое количество кислорода может вытечь, если выпуск производить очень медленно при постоянной температуре газа и конечном давлении Р2 = 7,0 МПа?
Ответ: после выпуска t2 = - 33 oС;
выпущено DGад= 2,86 кг кислорода; Р2 = 8,55 МПа; при изотермическом выпуске DGазот = 3,68 кг.
5.16 Некоторый процесс расширения кислорода характеризуется тремя равновесными состояниями, для которых параметры имеют следующие значения:
1) р1 = 2 МПа, t1 = 487 oС;
2) р2 = 1 МПа, V2 = 0,213 м3/кг;
3) V3 = 0,300 м3/кг, t3 = 576 oС. Определить, является ли этот процесс политропным? Если да, то чему равен показатель политропы? Ответ: процесс политропный, n = 0,900.
5.17. При сжатии воздуха подведено 50 кДж/кг теплоты. В конце политропного процесса температура воздуха увеличилась на 100oС. Определить показатель политропы сжатия. Подсчитать процентное соотношение между работой, теплотой и изменением внутренней энергии. Изобразить в P,Vдиаграмме примерный ход процесса.
Ответ: n = 2,316; Q = 69,6 %;
DU= 30,4 %.
6 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Первый закон термодинамики, устанавливая эквивалентность различных форм энергии, соотношение между изменением внутренней энергии системы, количеством подведенной теплоты и совершенной работы, не позволяет в то же время решить вопрос о возможности осуществления того или иного процесса, о направлении его развития и о глубине его протекания.
Превращение работы в теплоту происходит всегда полностью и безусловно: обратный же процесс превращения теплоты в работу при непрерывном ее переходе возможен лишь при некоторых определенных условиях и при том же всегда полностью.
Для более полного анализа явлений и процессов необходимо к первому закону термодинамики добавить еще одну общую закономерность, позволяющую определить их качественные особенности. Этой цели служит второй закон термодинамики, который устанавливает, возможен или невозможен тот или иной процесс, в каком преимущественном направлении он будет протекать, когда система достигает термодинамического равновесия, и при каких условиях от системы можно получить максимальную работу
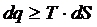
Это соотношение, справедливое и для обратимых (знак равенства) и для необратимых (знак неравенства) процессов в любой системе, и представляет собой аналитическое выражение второго закона термодинамики.
ЗАДАЧИ
6.1 Определить термический к.п.д. четырехпроцессного цикла, если работа и теплота, участвующие в каждом процессе, равны:
Процесс.............. 1 2 3 4
l,кДж/кг........... 3 10 -8 0
q,кДж/кг........... 30 -10 -20 5
Ответ: zt= 0,143.
6.2 Определить термический к.п.д. теплового двигателя, работающего по обратимому циклу Карно. Температура подвода тепла 500 oС, температура отвода тепла 20 oС. Определить также, сколько подводится и сколько отводится теплоты в этом двигателе, если мощность его/N = 5 МВт.
Ответ:zt = 0,621; q1= 8060 кДж/с; q2 = 3060 кДж/с.
6.3 30 л воды при температуре 90 oС смешивается с 20 л воды при температуре 15 oС.
Определить вызванное этим процессом изменение энтропии. Теплоемкость воды принять равной 4,178 кДж/кг К. Считать, что тепловые потери отсутствуют.
Ответ: DS = 1,41 кДж/кг.
6.4 Стальной шар массой 10 кг при 500 oС погружают в сосуд с 18 кг воды, температура которой равна 15 oС.
Определить изменение энтропии системы в этом процессе. Считать, что тепловые потери отсутствуют. Теплоемкость стали принять равной 0,5129 кДж/кг К, теплоемкость воды 4,187 кДж/кг К.
Ответ: DS = 3,13 кДж/К.
6.5 Камень массой G = 1,2 кг падает с высоты h = 14 м на землю.
Определить вызванное этим изменение энтропии системы камень-земля. Температура камня и окружающей среды равна 20 oС.
Решение. Изменение энтропии системы в данном необратимом процессе можно вычислить из формулы потери работоспособности. Потеря работоспособности равна убыли потенциальной энергии, т.е.  , отсюда
, отсюда 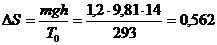 Дж/К.
Дж/К.
6.6 Определить, на сколько увеличится энтропия при смешении 3 кг азота и 2 кг углекислого газа. Газы считать идеальными. Температура, давление газов до смешения одинаковы. Ответ: DS = 0,7725 кДж/К.
6.7 Холодильная установка холодопроизводительностью 25140 кДж/г создает температуру в охлажденном помещении t = -10 oС. Температура помещения, в котором стоит холодильная установка, работает по обратимому циклу Карно, определить холодильный коэффициент x, количество теплоты 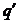 , которое передает установка верхнему тепловому источнику (среде) в процессе при t = 20oС, и теоретическую мощность привода установки.
, которое передает установка верхнему тепловому источнику (среде) в процессе при t = 20oС, и теоретическую мощность привода установки.
Определить, будет нагреваться или охлаждаться помещение после включения холодильной установки, и количество теплоты  которое будет подводиться (или отводиться) к воздуху в комнате.
которое будет подводиться (или отводиться) к воздуху в комнате.
Ответ: x = 8.77; Nтеор= 0,794 кВт; 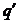 = 27,98 МДж/ч;
= 27,98 МДж/ч;  = 2,86 МДж/ч. Помещение будет нагреваться.
= 2,86 МДж/ч. Помещение будет нагреваться.
6.8 Двигатель расходует на 1 л.с. в час 162 г топлива с теплотой сгорания 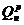 = 10200 ккал/кг = 42738 кДж/кг.
= 10200 ккал/кг = 42738 кДж/кг.
Определить к.п.д. этого двигателя и сравнить его с к.п.д. цикла Карно, если максимальная температура в процессе горения 1500 oС, температура окружающей среды 20 oС.
Ответ: z = 0,383; zк = 0,835.
6.9 Рассчитать цикл Карно, для которого Р1 = 1 МПа; t1 = 250 oС;
Р3 = 0,12 МПа; t3 = 30 oС рисунок 6.1 Рабочее тело -воздух. Рассчитать цикл, это значит найти параметры всех точек (P,V,T), количество подведенного и отведенного тепла, полезное тепло и полезную работу, а также термический к.п.д. цикла.
 P
P

 |
V
Рисунок 6.1 - Цикл Карно
Ответ: V1 = 0,153 м3/кг; V2= 0,189 м3/кг;
V4 = 0,6 м3/кг; q1=32,263 кДж/кг;zt= 0,42; V3 = 0,739 м3/кг;
Р2 = 0,8 МПа; Р4 = 0,1 МПа; q2 = 18,64 кДж/кг.
6.10 2 кг воздуха совершают цикл Карно в следующих пределах: P1 = 4 МПа; Т1 = 700 К; P3 = 0,11 МПа; T3 = 300 К. Рассчитать цикл.
Ответ: V1 = 0,142; V3 = 3,05 м3; P4= 0,624 МПа; zt= 0,415.
6.11 Цикл Карно совершается в пределах t1= 150oС и t2= 5 oС. Определить использованное и отданное низшему источнику количество тепла, если из верхнего получено q1 = 419 кДж/кг. Ответ: 143,3 кДж/кг.
6.12 В цикле Карно используется qn = 420 кДж/кг тепла, причем в низший источник отводится q2 = 167,6 кДж/кг. Определить термический к.п.д. и верхний предел температур, если низший предел составляет Т2 = 300 К.
Ответ: 0,715; 1050 К.
6.13 Определить эксергию теплоты, которая выделяется при сгорании на воздухе 1 кг топлива теплотой сгорания 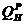 = 20 МДж/кг. Температура сгорания 1300 oС. Параметры среды: Р0 = 0,1 МПа; t0= 20 oС. Теплоемкость продуктов сгорания принять постоянной.
= 20 МДж/кг. Температура сгорания 1300 oС. Параметры среды: Р0 = 0,1 МПа; t0= 20 oС. Теплоемкость продуктов сгорания принять постоянной.
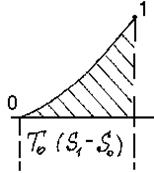
Решение. Получившийся источник теплоты является источником теплоты с переменной температурой, так как в процессе отвода теплоты от источника и превращения теплоты в работу он будет охлаждаться; его работоспособность будет исчерпана, когда его температура станет равной температуре среды. На рисунке 6.2 показан процесс охлаждения источника теплоты линией 1 - 0 до температуры среды Т0.
 T
T
 |
 S
S
Рисунок 6.2 - Процесс охлаждения
Эксергия будет определяться следующим образом. Для бесконечно малого количества теплоты при температуре Т дифференциал эксергии определяется через термический к.п.д. цикла Карно, т.е. 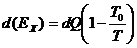 , тогда эксергия оказывается равной:
, тогда эксергия оказывается равной: 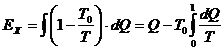 ;
;  .
.
На рис. 6.2 эксергия численно равна заштрихованной площади согласно приведенной выше формуле.
Величина 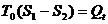 равна тому количеству теплоты, которое надо передать нижнему источнику (среде) в процессе превращения теплоты в
равна тому количеству теплоты, которое надо передать нижнему источнику (среде) в процессе превращения теплоты в
работу. Изменение энтропии может быть вычислено так: 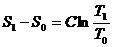
где С - теплоемкость данного источника теплоты:
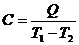 .
.
С учетом написанных соотношений эксергия теплоты может быть вычислена по формуле: 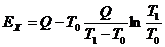 ;
;
окончательно 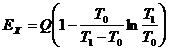 .
.
Вычислим значение эксергии по этой формуле:
 МДж.
МДж.
Таким образом, эксергия теплоты в данных условиях составляет 61,5 % теплоты сгорания топлива.
6.14 Определить эксергию количества теплоты, которая получается в результате сгорания на воздухе 1 кг топлива с теплотой сгорания 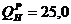 МДж/кг; температура сгорания 1500 oС; температура окружающей среды t0= 20 oС; теплоемкость продуктов сгорания принять постоянной. Ответ:EX = 16,08 МДж/кг, что составляет 64,3 % теплоты сгорания топлива.
МДж/кг; температура сгорания 1500 oС; температура окружающей среды t0= 20 oС; теплоемкость продуктов сгорания принять постоянной. Ответ:EX = 16,08 МДж/кг, что составляет 64,3 % теплоты сгорания топлива.
7 РАСЧЕТ ТЕРМОДИНАМИЧЕСКОГО ГАЗОВОГО ЦИКЛА
Условие задания
По заданным исходным параметрам рабочего тела для прямого
цикла, образованного заданными процессами, определить:
1. Параметры и функции состояния (P,v,T,h,u,s) в крайних точках цикла. Энтальпию и внутреннюю энергию определить относительно состояния Т0= 0 К, энтропию определить относительно состояния при нормальных условиях (Т0 = 273 К, Р0 = 0,101 ГПа).
2. Построить цикл в Р,v- и Т, s- координатах. Для построения кривых найти промежуточные точки.
3. Для каждого процесса определить работу, количество подведенного и отведенного тепла, изменение внутренней энергии, энтальпии и энтропии.
4. Определить работу цикла, количество подведенного и отведенного тепла, термический к.п.д. цикла. Сравнить последний с к.п.д. цикла Карно, имеющего одинаковые с расчетным циклом максимальное и минимальное значение температуры.
Рабочее тело - 1 кг газовой смеси.
Газовая смесь подчиняется уравнению состояния идеального газа.
При расчете теплоемкость считать зависящей от температуры.
Исходные данные для расчета принять в соответствии с номером задания из таблиц 7.1 и 7.2
Таблица 7.1 - Исходные данные для расчета циклов
| Предпослед-ние цифры задания | Исходные данные | Характеристика процессов | |||||||||||
| Р1=0,5 МПа; V2 = 0,09 м3/кг; P2=1,0 МПа; V3 = 0,14 м3/кг | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2>P1 | P=const | dq=0 | P=const | ||||||||||
| Р1=0,1 МПа; V2 = 0,4 м3/кг; Р2=0,2 МПа; V3 = 0,8 м3/кг | |||||||||||||
| Р1=0,3 МПа; V2 = 0,15 м3/кг; Р2=0,6 МПа; V3 = 0,5 м3/кг | |||||||||||||
| t1=200 oС; Р1=0,6 МПа; t2=300 oС V3=0,5 м3/кг; Р5 = 0,3 МПа | 1-2 | 2-3 | 3-4 | 4-5 | 5-1 | ||||||||
| P=const V2>V1 | T=const | V=const | P=const | V=const | |||||||||
| t1 =250 oС; Р1=0,8 МПа; t2=400 oС V3 =0,7 м3/кг; Р5 = 0,2 МПа | |||||||||||||
| t1=300 oС; Р1=1,0 МПа; t2=400 oC V3=0,35 м3/кг; Р5 = 0,2 МПа | |||||||||||||
| t1 =25 oС; Р1=0,3 МПа; Р2=2,0 МПа; t3 =550 oС | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | P=const | T=const | P=const | ||||||||||
| t1 =25 oС; Р1=0,15 МПа; Р2=2,0 МПа; t3 =500 oС | |||||||||||||
| t1 =30 oС; Р1=0,2 МПа; Р2=1,5 МПа; t3 = 600 oС | |||||||||||||
| Р1=0,3 МПа; V1=0,3 м3/кг; Р2=1,0 МПа; t3=200 oC | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | V=const | T=const | P=const | ||||||||||
| Р1=0,2 МПа; V1 = 0,5 м3/кг; Р2=1,0 МПа; t3 = 400 oC | |||||||||||||
| Р1=0,1 МПа; V1 = 0,9 м3/кг; Р2=0,5 МПа; t3 =1200oC | |||||||||||||
| P1=1,2 Мпа; V1=0,08 м3/кг; Р2=1,4 МПа; t3=160 oC | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| V=const P2>P1 | P=const | V=const | P=const | ||||||||||
| Р1=0,2 Мпа; V1 = 0,6 м3/кг; Р2=0,4 Мпа; t3 = 1000 oС | |||||||||||||
| Р1=0,6 Мпа; V1=0,15 м3/кг; Р2=0,9 Мпа; t3=360 oС | |||||||||||||
| V1 =0,12 м3/кг; t1=50 oС; Р2=2,5 МПа; t3=300 oС | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | P=const | T=const | P=const | ||||||||||
| V1 =0,12 м3/кг; t1=100 oC; Р2=2,0 МПа; t3=300 oС | |||||||||||||
| V1 =0,12 м3/кг; t1=150 oC; Р2=2,5 МПа; t3=850 oC | |||||||||||||
| Р1=0,2 МПа; Р2=1,0 Мпа; t2=300 °С; q2-3 =1050 кДж/кг | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | P=const | dq=0 | P=const | ||||||||||
| Р1=0,1 МПа; Р2=0,8 МПа; t2= 400 °С; q2-3=500 кДж/кг | |||||||||||||
| Р1=0,1 МПа; P2= 0,5 МПа; t2=300 °С; q2-3=800 кДж/кг | |||||||||||||
| Р1=0,08 МПа; t1=10 oС; V2= 0,4 м3/кг; t3= 227 °С | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2>P1 | T=const | dq=0 | V=const | ||||||||||
| P1=0,2 МПа; t1= 100 °С; V2=0,2 м3/кг; t3= 400 °С | |||||||||||||
| P1=0,3 МПа; t1= 10 oС; V2=0,1 м3/кг; t3=250 °С | |||||||||||||
P1=0,12 МПа; t1=55 oС; 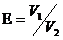 =15; q2-3=920 кДж/кг =15; q2-3=920 кДж/кг
| 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | P=const | dq=0 | V=const | ||||||||||
P1=0,12 МПа; t1=20°С; 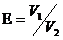 =12; q2-3=500 кДж/кг =12; q2-3=500 кДж/кг
| |||||||||||||
Р1=0,12 МПа; t1=40 °С;
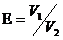 =8; q2-3=300 кДж/кг =8; q2-3=300 кДж/кг
| |||||||||||||
V1=1,1 м3/кг; t1=80 °С; 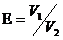 =14; q2-3=840 кДж/кг =14; q2-3=840 кДж/кг
| 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | P=const | T=const | V=const | ||||||||||
V1=1,1 м3/кг; t1=50 °С; 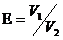 =16; q2-3=900 кДж/кг =16; q2-3=900 кДж/кг
| |||||||||||||
V1=1,1 м3/кг; t1=30 oС; 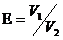 =12; q2-3=700кДж/кг =12; q2-3=700кДж/кг
| |||||||||||||
| P1=0,08 МПа; t1=10 °С; V2= 0,4 м3/кг; t3=225 oC | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2>P1 | V=const | dq=0 | V=const | ||||||||||
| Р1=0,12 МПа; t1=30 oС; V2 = 0,3 м3/кг; t3=250 °С | |||||||||||||
| Р1=0,2 МПа; t1= 50 °С; V2=0,1 м3/кг; t3=350 °С | |||||||||||||
V1=1,2 м3/кг; t1=80 oС; 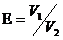 =5; q2-3=840 кДж/кг =5; q2-3=840 кДж/кг
| 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2>P1 | V=const | T=const | V=const | ||||||||||
V1 = 1,2 м3/кг; t1=120°С; 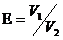 =6; q2-3=750 кДж/кг =6; q2-3=750 кДж/кг
| |||||||||||||
V1=1 м3/кг; t1=150 oС; 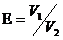 =9;q2-3=500 кДж/кг =9;q2-3=500 кДж/кг
| |||||||||||||
| P1 =3,0 МПа; t1= 400°С; Р2 = 1,4 МПа; P3 =0,6 МПа | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2<P1 | dq=0 | T=const | dq=0 | ||||||||||
| P1 = 3,0 МПа; t1= 450 °С; Р2 = 2,0 МПа; P3 =0,6 МПа | |||||||||||||
| Р1 = 3,0 МПа; t1=550 oС; Р2 = 2,0 МПа; Р3=0,5 МПа | |||||||||||||
| P1 =5,0 МПа; V2=0,12 м3/кг; P3 =0,5 МПа; t4= -35 °С | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2<P1 | dq=0 | T=const | dq=0 | ||||||||||
| P1=6,0 МПа; V2=0,14 м3/кг; P3 =0,5 МПа; t4= 20 oC | |||||||||||||
| P1=4,0 МПа; V2=0,12 м3/кг; P3=0,4 МПа; t4=10 oС | |||||||||||||
| P1=0,35 МПа; V1=0,25 м3/кг; Р2=2,0 МПа; t3=300 °С | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | P=const | dq=0 | V=const | ||||||||||
| P1=0,25 МПа; V1=0,4 м3/кг; P2=1,5 МПа; t3=370 °С | |||||||||||||
| P1=0,4 МПа; V1=0,3 м3/кг; Р2=2,5 МПа; t3=550 °С | |||||||||||||
| P1 = 1,3 МПа; t1 =300 °С; t3=17 °С; P3 =0,1 МПа | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2<P1 | dq=0 | T=const | dq=0 | ||||||||||
| P1 = 1,7 МПа; t1= 350 °С; t3= 30 oС; P3 = 0,12 МПа | |||||||||||||
| P1 = 1,0 МПа; t1= 300 °С; t3= 20 °С; P3 = 0,5 МПа | |||||||||||||
| P1 = 0,2 МПа; V1 = 0,45 м3/к; P3 = 1,2 МПа; V2= 0,14 м3/кг | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | V=const | dq=0 | P=const | ||||||||||
| P1 = 0,2 МПа; V1= 0,45 м3/кг; P3 = 1,5 МПа; V2= 0,14 м3/кг | |||||||||||||
| P1 = 0,1 МПа; V1= 0,6 м3/кг; P3 =1,0 МПа; V2= 0,15 м3 /кг | |||||||||||||
| P1 = 3,5 МПа; t1= 210 °С; t2= 250 °С; P3 = 2,5 МПа | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| P=const P2>P1 | dq=0 | P=const | V=const | ||||||||||
| P1 = 2,0 МПа; t1= 210 °С; t2= 250 °С; P3 = 1,8 МПа | |||||||||||||
| P1 = 1,5 МПа; t1 = 250 °С; t2= 350 °С; P3 = 1,0 МПа | |||||||||||||
P1=0,1 МПа; t1=-50 °С; n=1,2; Р2=0,5 МПа; 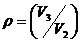 =2 =2
| 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| PVn=const P2>P1 | P=const | PVn=const | P=const | ||||||||||
P1 = 0,1 МПа; t1=10 °С; n=1,2;
P2 = 0,7 МПа; 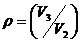 = 2 = 2
| |||||||||||||
P1=0,12 МПа; t1=30 °С; n=1,25;
P2 = 1,0 МПа; 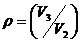 =1,8 =1,8
| |||||||||||||
| P1 = 0,12 МПа; V1 = 0,5 м3/кг; t2=130 °С; P3=4,0 МПа | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | V=const | dq=0 | P=const | ||||||||||
| P1 = 0,1 МПа; V1 = 0,7 м3/кг; t2 = 150 °С; P3 = 4,0 МПа | |||||||||||||
| P1 = 0,08 МПа; V1 =0,75 м3/кг; t1=150 °С; P3 = 4,5 МПа | |||||||||||||
| P1 = 0,18 МПа;, t2= 300 oС; V2 = 0,5 м3/кг; P3 = 0,25 МПа | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| PV1,2=const P2>P1 | T=const | PV1,2=const | V=const | ||||||||||
| P1 = 0,2 МПа; t2= 350 °С; V2=0,2 м3/кг; P3 = 0,7 МПа | |||||||||||||
| P1 = 0,15 МПа; t2= 300 °С; V2 = 0,6 м3/кг; P3 = 0,23 МПа | |||||||||||||
| P1 = 0,1 МПа; t1= 50 oС; Р2 = 1,0 МПа; t3= 200 °С | 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| T=const P2>P1 | P=const | T=const | P=const | ||||||||||
| Р1 = 0,1 МПа; t1= 20 °С; Р2 = 1,2 МПа; t3 = 250 °С | |||||||||||||
| P1 = 0,2 МПа; t1 = 50 °С; P2 = 0,8 МПа; t3 = 300 oС | |||||||||||||
P1 = 0,1 МПа; T1 = 300 К. 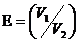 =16; =16; 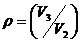 =4 =4
| 1-2 | 2-3 | 3-4 | 4-1 | |||||||||
| dq=0 P2>P1 | T=const | dq=0 | V=const | ||||||||||
P1 = 0,1 МПа; T1 = 320 К. 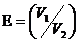 =14; =14; 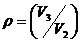 =3 =3
| |||||||||||||
P1= 0,2 МПа; T1 = 300 К; 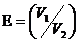 = 15; = 15; 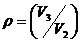 =2 =2
| |||||||||||||
| P1 = 0,1 МПа; t1= 27 °С; Р2= 0,8 МПа; q2-3=620 кДж/кг | 1-2 | 2-3 | 3-4 | 4-1 | |||
| T=const P2>P1 | V=const | T=const | V=const | ||||
| P1 = 0,2 МПа; t1= 50 °С; Р2=1,0 МПа; q2-3= 600 кДж/кг | |||||||
| P1 = 0,3 МПа; t1= 20 °С; Р2=1,5 Мпа; q2-3=700 кДж/кг | |||||||
| P1 = 1,2 Мпа; t1= 100 oС; Р2 = 3,0 Мпа; t3= 200 oС | 1-2 | 2-3 | 3-4 | 4-1 | |||
| T=const P2>P1 | P=const | T=const | P=const | ||||
| P1 = 0,2 Мпа; t1= 100 °С; Р2 = 1,0 Мпа; t3= 200 oС | |||||||
| P1 = 0,6 Мпа; t1= 150 °С; Р2 = 1,5 Мпа; t3= 250 oС | |||||||
| P1 = 5,0 Мпа;t1= 300 oС; Р2 = 1,8 Мпа; V3= 0,1 м3/кг | 1-2 | 2-3 | 3-4 | 4-1 | |||
| dq=0 P2>P1 | T=const | dq=0 | V=const | ||||
| P1 = 2,5 Мпа; t1= 300 oС; P2 = 1,25 Мпа; V3 = 0,2 м3/кг | |||||||
| P1 = 1,0 Мпа; t1= 300 °С; Р2 = 0,5 Мпа; V3= 0,4 м3/кг | |||||||
| P1 = 2,4 Мпа; V1=0,04м3/кг; Р2 = 2,8 Мпа; t3 = 150 °С | 1-2 | 2-3 | 3-4 | 4-1 | |||
| V=const P2>P1 | P=const | V=const | P=const | ||||
| P1 = 1,5 Мпа; V1=0,08 м3/кг; Р2 = 1,9 Мпа; t3= 300 °С | |||||||
| P1 = 1,0 Мпа; V1=0,12 м3/кг; Р2 = 1,5 Мпа; t3= 700 °С | |||||||
| t1=210 °С; Р1=1,0 Мпа; t2=300°С; V3 = 0,2 м3/кг; Р4 = 0,6 Мпа | 1-2 | 2-3 | 3-4 | 4-5 | 5-1 | ||
| P=const V2>V1 | dq=0 | V=const | P=const | V=const | |||
| t1=200 oC; P1=1,5 Мпа; t2=300°C; V3 = 0,2 м3/кг; Р4 = 0,4 Мпа | |||||||
| t1=200 °С; P1=2,0 Мпа; t2=300°С; V3= 0,2 м3кг; Р4 = 0,5 Мпа | |||||||
| V1= 0,12 м3/кг; Р1= 0,8 Мпа; Р2 = 2,0 Мпа; P3 = 1,2 Мпа | 1-2 | 2-3 | 3-4 | 4-1 | |||
| dq=0 P2>P1 | T=const | dq=0 | V=const | ||||
| V1 =0,15 м3/кг; P1 = 0,7 Мпа; Р2 = 2,5 Мпа; P3 = 2,0 Мпа | |||||||
| V1= 0,8 м3/кг; P1 = 1,0 Мпа; Р2 = 3,0 Мпа; P3 = 2,5 Мпа |
Окончание таблицы 7.1
t3= 27 oС; Р3 = 0,1 МПа;
 = 3; q1-2 = 220 кДж/кг = 3; q1-2 = 220 кДж/кг
| 1-2 | 2-3 | 3-4 | 4-1 | |||
| T=const P2>P1 | dq=0 | T=const | dq=0 | ||||
t3 = 50 °C; P3 = 0,13 МПа;  =4; q1-2= 300 кДж/кг =4; q1-2= 300 кДж/кг
| |||||||
t3 = 50 °C; P3 = 0,08 МПа;
 = 5; q1-2 = 300 кДж/кг = 5; q1-2 = 300 кДж/кг
| |||||||
P1 = 0,1 МПа; t1 = 20 °С; 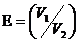 =6; =6; 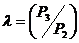 = 2 = 2
| 1-2 | 2-3 | 3-4 | 4-1 | |||
| dq=0 P2>P1 | V=const | dq=0 | V=const | ||||
P1 = 0,12 МПа; t1 = 40 °С; 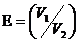 = 8; = 8; 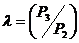 = 1,5 = 1,5
| |||||||
P1 = 0,12 МПа;t1 = 20 oС; 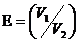 =10; =10; 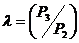 =1,8 =1,8
| |||||||
Р1 = 0,1 МПа; t1=30°С 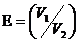 =5;q2-3=500кДк/кг =5;q2-3=500кДк/кг
| 1-2 | 2-3 | 3-4 | 4-1 | |||
| dq=0 P2>P1 | V=const | T=const | V=const | ||||
P1 = 0,13 МПа; t1 = 40oС; 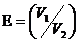 =7;q2-3=300 кДж/кг =7;q2-3=300 кДж/кг
| |||||||
P1 = 0.11 МПа; t1 = 50°С; 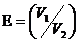 =10;q2-3=600кДж/кг =10;q2-3=600кДж/кг
| |||||||
P1 = 0,1 МПа; t1 = 15 °С; 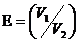 =16;q2-3=600кДж/кг =16;q2-3=600кДж/кг
| 1-2 | 2-3 | 3-4 | 4-1 | |||
| dq=0 P2>P1 | P=const | T=const | V=const | ||||
P1 = 0,11 МПа; t1 =15 °С; 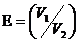 =14;q2-1=800кДж/кг =14;q2-1=800кДж/кг
| |||||||
Р1 = 0,12 МПа;t1 = 25 °С; 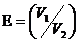 =18;q2-3=750кДж/кг =18;q2-3=750кДж/кг
|
Не нашли, что искали? Воспользуйтесь поиском: