
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задач. Пример 1. Определите потенциал ионизации и первый потенциал возбуждения атома водорода.
Пример 1. Определите потенциал ионизации и первый потенциал возбуждения атома водорода.
Решение.
Потенциалом ионизации Ui называют ту наименьшую разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с данным невозбужденным атомом ионизировать его. Работа по удалению электрона из атома Аi равна работе сил электрического поля, ускоряющего электрон, eUi, поэтому Аi=eUi.
Учитывая квантовый характер поглощения энергии атомом, можно сказать, что работа ионизации Аi равна кванту энергии hv, поглощенному атомом водорода при переходе электрона с первой боровской орбиты на бесконечно удаленную орбиту. Тогда, применив сериальную формулу Бальмера и положив в ней n 1 = 1; n 2 = ∞, получим:
 .
.
Следовательно
 ;
;
 .
.
Первый потенциал возбуждения U1 есть та наименьшая разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с невозбужденным атомом перевести его в первое возбужденное состояние. Для атома водорода это соответствует переходу электрона с первой боровской орбиты на вторую. Приравняв работу сил ускоряющего электрического поля eU1 кванту энергии hν, поглощенному атомом при его переходе в первое возбужденное состояние, получим:
 ,
,
где n 1=1, n 2=2. Откуда:
 .
.
Производим вычисления:
 .
.
Ответ: Ui = 13,6 В; U 1 = 10,2 В.
Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Определите длину волны де Бройля электрона для двух случаев: 1) U 1 = 51 В; 2) U 2 = 510 кВ.
| Дано: | Решение: |
| m 0 = 9,1×10-31 кг e = 1,6×10-19 Кл U 1 = 51 B U 2 = 510 кВ = 51×104 В | Длина волны де Бройля для частицы определяется формулой
 , (1)
где р – импульс частицы. , (1)
где р – импульс частицы.
|
| λ 1-? λ 2-? |
Импульс частицы связан с ее кинетической энергией Т соотношением:
1) в нерелятивистском (классическом) случае (когда кинетическая энергия частицы Т много меньше ее энергии покоя Е 0 = m 0 с2):
 , (2)
, (2)
где m 0 – масса покоя частицы;
2) в релятивистском случае (когда кинетическая энергия Т сравнима с энергией покоя Е 0 частицы):
 , (3)
, (3)
где с – скорость света в вакууме.
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U 1 = 51 В и U 2 =510 кВ, с энергией покоя электрона Е 0 = m 0 с 2 = 0,51 МэВ и в зависимости от этого решим, какую из формул (2) или (3) следует применить для вычисления длины волны де Бройля.
Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U 1 равна T = еU.
В первом случае
T 1= еU 1 = 1,6×10-19 Кл × 51 В = 81,6×10-19 Дж =
= 51 эВ = 0,51×10-4 МэВ,
что много меньше энергии покоя электрона Е 0 = 0,51 МэВ. Следовательно, в этом случае можно применять формулу (2). Тогда:

 .
.
Во втором случае кинетическая энергия
T 2 = еU 2 = 51×104 эВ = 0,51 МэВ,
т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (3). Тогда получим:
 ;
;
Так как Т 2 = Е 0 = m 0 c2, то получим:
 ;
;
Произведем вычисления:
 .
.
Ответ: λ 1 = 172 пм; λ 2 = 1,4 пм.
Пример 3. Используя соотношение неопределенностей Гейзенберга, показать, что ядра атомов не могут содержать электронов. Считать радиус ядра равным Rя = 10-13 см.
| Дано: | Решение: |
| Rя = 10-13 см = 10-15 м ħ = 1,05×10-34 Дж×с | Соотношение неопределенностей для координаты и импульса имеет вид |
Δ х· Δ рх ≥ ћ,
где Δ х – неопределенность координаты частицы (в данном случае электрона);
Δ рх – неопределенность импульса электрона;
ћ – постоянная Планка.
Если неопределенность координаты принять равной радиусу ядра, т.е. Δ х = Rя, то неопределенность импульса электрона выразим следующим образом:
 .
.
Так как Δ рх=mΔVх, то  и
и  .
.
Вычислим неопределенность скорости электрона:
 .
.
Сравнивая полученное значение  со скоростью света в вакууме с = 3×108 м/с, видим, что
со скоростью света в вакууме с = 3×108 м/с, видим, что  , а это невозможно. Следовательно, ядра не могут содержать электронов.
, а это невозможно. Следовательно, ядра не могут содержать электронов.
Пример 4. Электрон находится в бесконечно глубоком, прямоугольном, потенциальном ящике шириной l. В каких точках в интервале (0< х < l) плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить значение плотности вероятности для этих точек. Решение пояснить графиком.
| Дано: | Решение: |
0< х < l
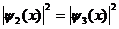
| Вероятность обнаружить частицу в интервале х 1< х < х 2 определяется выражением:
 , ,
|
х -?  -? -?
|
где ψn(х) – нормированная собственная ψ -функция, отвечающая данному состоянию. Нормированная собственная ψ -функция, описывающая состояние электрона в потенциальном ящике, имеет вид:
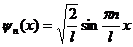 .
.
Возбужденным состоянием (n 1=2) и (n 2=3) отвечают собственные функции:
 и
и  .
.
По условию задачи 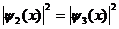 , тогда получим:
, тогда получим:
 , или
, или
 .
.
 .
.
Используя соотношения:
 ,
,
 ,
,
получим:
 ;
;
 . (*)
. (*)
Так как  , то выражение (*) примет вид:
, то выражение (*) примет вид:
 .
.
Решим полученное уравнение:
1)  , или
, или  , откуда
, откуда  , а
, а  , где n =0, 1, 2, 3,…
, где n =0, 1, 2, 3,…
Тогда 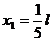 ;
;  ;
;  ;
;  .
.
2)  , или
, или  , откуда
, откуда  , а
, а  – это значение не удовлетворяет условию задачи (0< х < l).
– это значение не удовлетворяет условию задачи (0< х < l).
Следовательно, 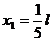 ;
;  ;
;  ;
;  .
.
Вычислим значение плотности вероятности в этих точках:
 .
.
Так как 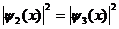 , то вычисление сделаем только для состояния n =2 (электрон находится на втором энергетическом уровне):
, то вычисление сделаем только для состояния n =2 (электрон находится на втором энергетическом уровне):
Для 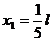 :
:
 ;
;
 :
:  ;
;
 :
:  ;
;
 :
:  .
.
Итак, для точек х 1 и х 4:  ;
;
Для точек х 2 и х 3:  .
.
Построим график (рисунок 54).

Пример 5. Определите начальную активность А 0 радиоактивного препарата магния 27 Mg массой m = 0,2 мкг, а также его активность А через время t = 6 ч. Период полураспада Т1/2 магния считать известным.
| Дано: | Решение: |
| 27 Mg m = 0,2 мкг = 2×10-10 кг М = 27×10-3 кг/моль t = 6 ч = 6×3,6×103 с Т 1/2 = 10 мин = 600 с | Активность А изотопа характеризует скорость радиоактивного распада и определяется отношением числа dN ядер, распавшихся за интервал времени dt, к этому интервалу: |
| А 0-? А -? |
 .
.
Знак «минус» показывает, что число N радиоактивных ядер с течением времени убывает.
Воспользуемся законом радиоактивного распада
N = N 0 е-λt.
Тогда:  .
.
Начальную активность А 0 препарата получим при t = 0: А 0 = λN 0, где постоянная радиоактивного распада  . Число N 0 радиоактивных ядер, содержащихся в изотопе массой m, равно:
. Число N 0 радиоактивных ядер, содержащихся в изотопе массой m, равно:  , где М – молярная масса изотопа. NА = 6,02×1023 моль-1 – постоянная Авогадро.
, где М – молярная масса изотопа. NА = 6,02×1023 моль-1 – постоянная Авогадро.
Следовательно,  ;
;
 , или
, или  .
.
Произведем вычисления:
 .
.
 .
.
Ответ: А 0 = 5,15 ТБк; А = 81,5 Бк.
Пример 6. Вычислите дефект массы и энергию связи ядра  .
.
Решение.
Дефект массы ядра Δ m есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, то есть:
 , (1)
, (1)
где Z – атомный номер изотопа (число протонов в ядре);
А – массовое число (число нуклонов, составляющих ядро);
|
В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в нее входила масса mа нейтрального атома. Масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: mа = mя + Zmе, откуда mя = mа – Zmе. Тогда формула (1) примет вид:
 .
.
Замечая, что mp + me =  (масса атома водорода), окончательно получим:
(масса атома водорода), окончательно получим:
 .
.
Подставив в это выражение числовые значения масс в а.е.м. (см. табл. 15 и 17 Приложения), получим:
 а.е.м
а.е.м
Для вычисления энергии связи ядра воспользуемся формулой
Есв = 931Δ m (МэВ ):
Есв = 931×0,04216 МэВ = 39,2 МэВ.
Ответ:Δ m = 0,04216 а.е.м.; Есв = 39,2 МэВ.
Пример 7. При соударении α -частицы с ядром бора  произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода  . Определите порядковый номер и массовое число второго ядра, запишите символически ядерную реакцию и определите ее энергетический эффект.
. Определите порядковый номер и массовое число второго ядра, запишите символически ядерную реакцию и определите ее энергетический эффект.
Решение.
Обозначим неизвестное ядро символом  . Так как α -частица представляет собой ядро гелия
. Так как α -частица представляет собой ядро гелия  , запись реакции имеет вид:
, запись реакции имеет вид:
 .
.
Применив закон сохранения заряда, получим уравнение: 2+5=1+ Z, откуда Z =6. Применив закон сохранения числа нуклонов, получим уравнение: 4+10=1+ А, откуда А =13. Следовательно, неизвестное ядро является ядром атома изотопа углерода  . Теперь можем записать ядерную реакцию в окончательном виде:
. Теперь можем записать ядерную реакцию в окончательном виде:
 .
.
Энергетический эффект Q ядерной реакции определяется по формуле:
Q = 931[(mHe + mB) – (mH + mC)] МэВ.
Заменяя массы исходных ядер и массы ядер продуктов реакции массами нейтральных атомов (см. табл.15 Приложения) и подставив их в расчетную формулу, получим:
Q = 931[4,00260+10,01294) – (1,00783+13,00335)] МэВ = 4,06 МэВ.
Ответ: Q = 4,06 МэВ.
Пример 8. Определить энергию реакции 10 В (n,α)7 Li, протекающей в результате взаимодействия весьма медленных нейтронов с покоящимися ядрами бора. Найти также кинетические энергии продуктов реакции.
Решение.
Ядерная реакция 10 В (n,α)7 Li состоит в следующем. Ядро бора  , поглотив медленный нейтрон
, поглотив медленный нейтрон  , превращается в промежуточное ядро
, превращается в промежуточное ядро  . Последнее, будучи возбужденным, испускает α -частицу (т.е. ядро гелия
. Последнее, будучи возбужденным, испускает α -частицу (т.е. ядро гелия  ), превращаясь в ядро лития
), превращаясь в ядро лития  . В развернутом виде реакция записывается так:
. В развернутом виде реакция записывается так:
 .
.
Энергия ядерной реакции (или тепловой эффект реакции) Q определяется по формуле:
Q  Дж, (1)
Дж, (1)
или Q  МэВ.
МэВ.
Заменив массы покоя ядер атомов массами покоя самих атомов (см. табл. 15 Приложения), получим:
Q = 931(10,01294+1,00867–7,01601–
– 4,00260) МэВ = 2,8 МэВ.
Чтобы найти кинетические энергии продуктов реакции – ядра лития 7 Li и α -частицы, применим закон сохранения релятивистской энергии и закон сохранения импульса:
 , или
, или
 ;
;
с учетом равенства (1) получим:
Q  .
.
Из условия задачи следует, что величинами TB и Tn можно пренебречь. Тогда получим для суммы кинетических энергий частиц 7 Li и 4 Не:
TLi + THе = Q (2)
По закону сохранения импульса:  .
.
Полагая суммарный импульс частиц до реакции равным нулю, получим:
 .
.
Отсюда для модулей импульсов имеем:  .
.
Импульсы частиц и их кинетические энергии связаны соотношением  . Следовательно:
. Следовательно:
 (3)
(3)
Решаем систему уравнений (2), (3):
Т.к.  Q
Q  , то
, то  (Q
(Q  ),
),
 Q Þ
Q Þ  ;
;
 .
.
Произведем вычисления:
 .
.
 .
.
Ответ: Q = 2,8 МэВ; ТLi = 1,02 МэВ; ТНе = 1,78 МэВ.
Пример 9. Позитрон с кинетической энергией Т = 0,75 МэВ налетает на покоящийся свободный электрон. В результате аннигиляции возникает два γ-фотона с одинаковыми энергиями. Определите угол θ между направлениями из разлета.
| Дано: | Решение: |
| Т = 0,75 МэВ = 0,75×1,6×10-13 Дж m 0 = 9,1×10-31 кг e1 = e2 = e | Процесс аннигиляции электрона е- и позитрона е+ происходит по схеме е-+е+→γ+γ и подчиняется |
| θ -? |
 законам сохранения энергии и импульса. Согласно закону сохранения импульса, импульс позитрона
законам сохранения энергии и импульса. Согласно закону сохранения импульса, импульс позитрона  равен векторной сумме импульсов γ-фотонов
равен векторной сумме импульсов γ-фотонов  и
и  (рисунок 55):
(рисунок 55):  .
.
При этом  , где ε– энергия каждого γ-фотона.
, где ε– энергия каждого γ-фотона.
Из рисунка 55 получим:  , тогда:
, тогда:
 (*)
(*)
Чтобы вычислить угол θ, надо определить импульс позитрона 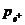 и энергию ε каждого γ-фотона. Импульс позитрона найдем, зная его кинетическую энергию Т. Поскольку величина Т превышает энергию покоя позитрона m 0 c 2 = 0,511 МэВ, то позитрон следует рассматривать как релятивистскую частицу. В этом случае импульс частицы выражается формулой
и энергию ε каждого γ-фотона. Импульс позитрона найдем, зная его кинетическую энергию Т. Поскольку величина Т превышает энергию покоя позитрона m 0 c 2 = 0,511 МэВ, то позитрон следует рассматривать как релятивистскую частицу. В этом случае импульс частицы выражается формулой  .
.
Энергию γ-фотона ε определим с помощью закона сохранения релятивистской энергии:
 ,
,
где  – сумма энергий покоя частиц до реакции, а
– сумма энергий покоя частиц до реакции, а  – сумма их кинетических энергий. Справа стоят величины, относящиеся к частицам после реакции. Учитывая, что масса покоя фотонов равна нулю:
– сумма их кинетических энергий. Справа стоят величины, относящиеся к частицам после реакции. Учитывая, что масса покоя фотонов равна нулю:  , а полная энергия фотонов есть их кинетическая энергия, т.е.
, а полная энергия фотонов есть их кинетическая энергия, т.е.  , и что электрон и позитрон обладают одинаковой массой покоя m 0, получим:
, и что электрон и позитрон обладают одинаковой массой покоя m 0, получим:  .
.
Подставив в уравнение (*) значение 2εи значение импульса позитрона 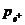 , найдем:
, найдем:
 .
.
Так как энергия покоя электрона (позитрона) m 0 c 2 = 0,511 МэВ, то получим:
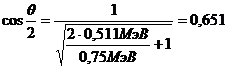 ;
;  .
.
Ответ: θ = 99°.
Не нашли, что искали? Воспользуйтесь поиском: