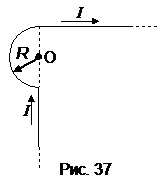ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основные законы и формулы. · Закон Био-Савара-Лапласа для элемента проводника с током
· Закон Био-Савара-Лапласа для элемента проводника с током
 , или
, или  ,
,
где m – магнитная проницаемость изотропной среды;
m 0 – магнитная постоянная (m 0 = 4 p ×10-7 Гн/м);
 – радиус-вектор, направленный от элемента проводника
– радиус-вектор, направленный от элемента проводника  к точке, в которой определяется магнитная индукция
к точке, в которой определяется магнитная индукция  поля;
поля;
α – угол между радиусом-вектором и направлением тока в элементе провода.
· Магнитная индукция поля, созданного:
а) бесконечно длинным прямым проводником с током
 ,
,
где r 0 – расстояние от оси провода до точки, в которой определяется магнитная индукция;
б) в центре кругового витка с током
 ,
,
где R – радиус витка;
в) отрезком проводника с током (рис. 21,а)
 .
.
Обозначения ясны из рисунка.

|

|

|
|
|
|
|
|
 , тогда
, тогда
 .
.
г) бесконечно длинным соленоидом на его оси (внутри соленоида)
 ,
,
где n – отношение числа витков соленоида к его длине.
д) на оси кругового тока
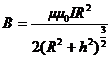 ,
,
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
· Связь магнитной индукции  с напряженностью
с напряженностью 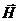 магнитного поля
магнитного поля
 .
.
· Сила действующая на прямой провод с током в однородном магнитном поле (закон Ампера)
 , или
, или 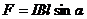 ,
,
где l – длина провода;
a – угол между направлением тока в проводе и вектором магнитной индукции  .
.
Если поле неоднородно и провод не является прямым, то:

где  – элемент провода с током I.
– элемент провода с током I.
· Магнитный момент плоского контура с током I:
 ,
,
где 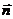 – единичный вектор нормали к плоскости контура, направление которой определяется в соответствии с правилом буравчика;
– единичный вектор нормали к плоскости контура, направление которой определяется в соответствии с правилом буравчика;
S – площадь контура.
· Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле
 ,или
,или  ,
,
где α – угол между векторами  и
и  .
.
· Сила Лоренца
 , или
, или 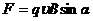 ,
,
где  – скорость заряженной частицы;
– скорость заряженной частицы;
α – угол между векторами  и
и  .
.
Если заряженная частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение:
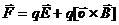 .
.
· Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
 , или
, или  ,
,
где S – площадь контура;
α – угол между нормалью 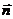 к плоскости контура и вектором магнитной индукции
к плоскости контура и вектором магнитной индукции  ;
;
б) в случае неоднородного поля и произвольной поверхности:
 ,
,
(интегрирование ведется по всей поверхности).
· Потокосцепление (полный поток)
 .
.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
· Работа по перемещению замкнутого контура с током в магнитном поле
 .
.
· Основной закон электромагнитной индукции (закон Фарадея)
 .
.
· ЭДС самоиндукции
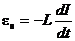 .
.
· Индуктивность контура
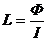 .
.
· Индуктивность соленоида, имеющего N витков
 , или
, или  ,
,
где  – отношение числа витков соленоида к его длине;
– отношение числа витков соленоида к его длине;
 – объем соленоида.
– объем соленоида.
· Разность потенциалов на концах провода длиной l, движущегося со скоростью  в магнитном поле
в магнитном поле
 ,
,
где α - угол между векторами  и
и  .
.
· Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур
 , или
, или 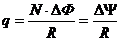 ,
,
где R – сопротивление контура.
· Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) при замыкании цепи
 ,
,
где  – сила тока цепи при t = 0;
– сила тока цепи при t = 0;
t – время, прошедшее после замыкания цепи.
б) при размыкании цепи
 ,
,
где t – время, прошедшее с момента размыкания цепи.
· Энергия магнитного поля
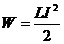 .
.
· Объемная плотность энергии магнитного поля
 ,
,
где B – магнитная индукция;
H – напряженность;
V – объем магнитного поля.
· Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора  )
)
 .
.
· Циркуляция вектора напряженности 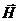 магнитного поля вдоль замкнутого контура, охватывающего ток I (закон полного тока для тока проводимости)
магнитного поля вдоль замкнутого контура, охватывающего ток I (закон полного тока для тока проводимости)

 ,
,
где Hl – проекция вектора напряженности 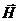 на направление касательной к контуру, содержащей элемент dl;
на направление касательной к контуру, содержащей элемент dl;
I – сила тока, который охватывается контуром.
· Период собственных электромагнитных колебаний в контуре (формула Томпсона)
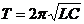 ,
,
где L – индуктивность;
C – электроемкость контура.
При наличии потерь в контуре (при наличии омического сопротивления R) собственные колебания являются затухающими, причем период колебаний
 ,
,
а сила тока в контуре изменяется по закону затухающих колебаний:
 .
.
· Скорость распространения электромагнитных волн в среде
 ,
,
где с – скорость электромагнитных волн в вакууме (с = 3×108 м/с);
e – диэлектрическая проницаемость среды;
m – магнитная проницаемость среды.
|
Примеры решения задач
Пример 1. Два параллельных бесконечно длинных провода А и С, по которым текут в одном направлении токи силой I 1 = I 2 = I = 50 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию  поля, создаваемого проводниками с током в точке D, отстоящей от оси одного провода на расстоянии r 1 = 5 см, от другого – на r 2= 12 см.
поля, создаваемого проводниками с током в точке D, отстоящей от оси одного провода на расстоянии r 1 = 5 см, от другого – на r 2= 12 см.
| Дано: | Решение: |
| I 1 = I 2 = I = 50 А d = 10 см = 0,10 м r 1 = 5 см = 0,05 м r 2 = 12 см = 0,12 м | Воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций  и и  полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
|
 -? -?
|

 .
.
Модуль вектора В может быть найден по теореме косинусов:
 ,
,
где α – угол между векторами  и
и  .
.
|
 ;
;  .
.
Тогда 
 . (*)
. (*)
Угол α =ÐADC – как углы при вершинах треугольников с взаимно перпендикулярными сторонами.
Из DАDС по теореме косинусов запишем:
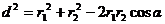 , откуда
, откуда  .
.
Подставим числовые значения и произведем вычисления:
 .
.
Подставив в формулу (*) числовые значения физических величин, получим:
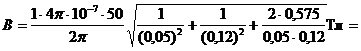

Ответ: В = 357,1 мкТл.
Пример 2. Изолированный прямолинейный проводник изогнут в виде прямого угла со стороной l = 20 см. В плоскости угла помещен кольцевой проводник радиусом R = 10 см так, что стороны угла являются касательными к нему (рисунок 23, а). Найти индукцию магнитного поля в центре кольца. Силы токов в проводниках одинаковы и равны I = 2 А. Влияние проводящих проводов не учитывать.
|
| Дано: | Решение: |
| l = 20 см = 0,20 м R = 10 см = 0,10 м I 1 = I 2 = I = 2 А | Воспользуемся законом Био-Савара-Лапласа и принципом суперпозиции магнитных полей. Вектор магнитной индукции суммарного поя в точке О
 , ,
|
| В -? |
где  – индукция магнитного поля, создаваемого прямолинейным проводником, согнутым в виде прямого угла;
– индукция магнитного поля, создаваемого прямолинейным проводником, согнутым в виде прямого угла;
 – кругового проводника радиусом R.
– кругового проводника радиусом R.
Эти векторы перпендикулярны плоскости, в которой лежат прямой проводник АВ и круговой проводник радиусом R = r 0, и совпадают по направлению (направлены на нас). Магнитная индукция, создаваемая в точке М конечным отрезком АВ прямого проводника на расстоянии r 0 от него (рисунок 23,б) равна  . Заметим, что при симметричном расположении точки М относительно отрезка АВ провода эта формула примет вид:
. Заметим, что при симметричном расположении точки М относительно отрезка АВ провода эта формула примет вид:
 ,
,
так как  , а α 1 = 45°.
, а α 1 = 45°.
Индукция от двух сторон угла составляет:
 , где
, где 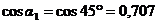
Индукция магнитного поля в центре окружности радиуса R=r 0 равна
 .
.
Результирующая индукция магнитного поля в центре кольца
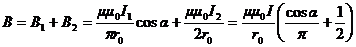 .
.
Произведем вычисления:
 (Тл).
(Тл).
Ответ: В =18,2×10-6 Тл=18,2 мкТл.
Пример 3. По тонкому проводящему кольцу радиусом R = 10 см течет ток I = 80 А. Найти магнитную индукцию  в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см.
в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см.
 |
| Дано: | Решение: |
| R = 10 см = 0,10 м I = 8 А r = 20 см = 0,20 м | Выделим на кольце элемент проводника dl с током I и от него в точку А проведем радиус-вектор  (рисунок 24). Вектор (рисунок 24). Вектор  магнитной индукции поля, создаваемого элементом тока магнитной индукции поля, создаваемого элементом тока  в точке А, направим в соответствии с правилом буравчика. в точке А, направим в соответствии с правилом буравчика.
|
Согласно принципу суперпозиции магнитных полей, магнитная индукция  в точке А определяется интегрированием:
в точке А определяется интегрированием:
 ,
,
где интегрирование ведется по всем элементам dl кольца.
Разложим вектор  на две составляющие:
на две составляющие:  , параллельную плоскости кольца, и
, параллельную плоскости кольца, и  перпендикулярную плоскости кольца, т. е.
перпендикулярную плоскости кольца, т. е.
 .
.
Тогда  .
.
В силу симметрии  . Векторы
. Векторы  от различных элементов dl сонаправлены, поэтому скалярное значение вектора
от различных элементов dl сонаправлены, поэтому скалярное значение вектора  будет равно:
будет равно:
 ,
,
где  и
и 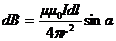 (по закону Био-Савара-Лапласа). Так как вектор
(по закону Био-Савара-Лапласа). Так как вектор  перпендикулярен
перпендикулярен  , то sin α =1. Следовательно,
, то sin α =1. Следовательно,
 ,
,
где  (рис. 24).
(рис. 24).
Тогда получим:  .
.
Проверим размерность искомой величины  :
:

 .
.
Произведем вычисления:

Ответ: Вектор  направлен по оси кольца (пунктирная стрелка на рисунке 24) и численно равен 62,8 мкТл.
направлен по оси кольца (пунктирная стрелка на рисунке 24) и численно равен 62,8 мкТл.
Пример 4. По тонкому стержню длиной l = 50 см равномерно распределен заряд q = 60 нКл. Стержень вращается с частотой ν = 12 с–1 относительно оси, перпендикулярной стержню и проходящей через стержень на расстоянии а = 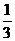 l от одного из его концов. Определить магнитный момент Pm, обусловленный вращением стержня.
l от одного из его концов. Определить магнитный момент Pm, обусловленный вращением стержня.
| Дано: | Решение: |
l =50 см = 0,50 м
q = 60 нКл = 60×10-9 Кл
ν = 12 с–1
а = 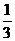 l l
| По определению магнитный момент плоского контура с током I равна
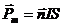 ,
где ,
где 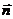 – единичный вектор нормали к плоскости контура S.
Выделим элемент стержня длиной – единичный вектор нормали к плоскости контура S.
Выделим элемент стержня длиной
|
| Pm -? |
dr с зарядом на нем  . При вращении стержня относительно оси О элементарный круговой ток в данном случае определяется выражением
. При вращении стержня относительно оси О элементарный круговой ток в данном случае определяется выражением
 ,
,
где n - частота вращения стержня. Магнитный момент элементарного кругового тока dPm = S×dI, где S – площадь, ограниченная окружностью, описываемой элементом стержня dr с зарядом dq (S = pr 2, где r – радиус этой окружности (рис. 25)).
 Тогда
Тогда  .
.
Магнитный момент Pm, обусловленный вращением стержня длиной l вокруг оси О, определяем интегрированием двух частей стержня:
 ,
,
где 0,  и
и  – пределы интегрирования.
– пределы интегрирования.

 .
.
 .
.
Произведем вычисления:
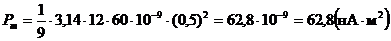 .
.
Ответ: Pm = 62,8 нА×м2.
 Пример 5. Длинный провод с током I = 50 А изогнут под углом α = 120°. Определить магнитную индукцию
Пример 5. Длинный провод с током I = 50 А изогнут под углом α = 120°. Определить магнитную индукцию  в точке А (рисунок 26). Расстояние
в точке А (рисунок 26). Расстояние
d = 5 см.
|
| Дано: | Решение: |
| I = 50 A α = 120° d = 5 см = 5×10-2 м | Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О (рисунок 27). В соответствии с принципом суперпозиции магнитных полей магнитная индукция  в точ- в точ-
|
 -? -?
|
|
 ке А будет равна геометрической сумме магнитных индукций
ке А будет равна геометрической сумме магнитных индукций  и
и  полей, создаваемых отрезком длинных проводов 1 и 2, т.е.
полей, создаваемых отрезком длинных проводов 1 и 2, т.е.  . Магнитная индукция
. Магнитная индукция  равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси провода,
равна нулю. Это следует из закона Био-Савара-Лапласа, согласно которому в точках, лежащих на оси провода,  ; (
; ( ; у нас
; у нас  ).
).
Магнитную индукцию В 1 найдем, воспользовавшись выражением для магнитной индукции поля, создаваемого отрезком провода с током I:
 ,
,
где r 0 – кратчайшее расстояние от провода 1 до точки А. В нашем случае α 1®0 (провод длинный),  , α 2 = α = 120° (cos α 2 = cos 120° = =
, α 2 = α = 120° (cos α 2 = cos 120° = =  ). Расстояние
). Расстояние

Тогда магнитная индукция
 .
.
Так как 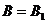 (B 2=0), то
(B 2=0), то  .
.
Вектор  сонаправлен с вектором
сонаправлен с вектором  и определяется правилом правого винта. На рисунке 27 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас)
и определяется правилом правого винта. На рисунке 27 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас)
Проверим, дает ли правая часть равенства единицу магнитной индукции (Тл):

|
 .
.
Ответ: В =173 мкТл.
Пример 6. Бесконечно длинный провод с током I = 80 А изогнут так, как это изображено на рисунке 28. Определить магнитную индукцию  в точке О. Радиус дуги R = 10 см.
в точке О. Радиус дуги R = 10 см.
  Дано: Дано:
| Решение: |
| I = 80 A R = 10 см = 0,1 м | Магнитную индукцию  в точке О найдем, используя принцип суперпозиции магнитных полей: в точке О найдем, используя принцип суперпозиции магнитных полей:
 . .
|
 -? -?
|
Разобьем провод на пять частей (рисунок 29): три прямолинейных (1,3 и 5) и две дуги полуокружностей (2 и 4) радиусами R и 2 R. Тогда
 ,
,
где  ,
,  ,
,  ,
,  и
и  – магнитные индукции поля в точке О, создаваемые током I, текущим на выделенных пяти участках длинного провода. Так как точка О лежит на оси проводов 1 и 3, то
– магнитные индукции поля в точке О, создаваемые током I, текущим на выделенных пяти участках длинного провода. Так как точка О лежит на оси проводов 1 и 3, то  и
и  . Тогда
. Тогда  .
.
Учитывая, что в соответствии с правилом буравчика векторы  и
и  направлены перпендикулярно плоскости чертежа на нас, вектор
направлены перпендикулярно плоскости чертежа на нас, вектор  – перпендикулярно плоскости чертежа от нас, векторную сумму можно заменить алгебраической: В = В 4+ В 5 – В 2.
– перпендикулярно плоскости чертежа от нас, векторную сумму можно заменить алгебраической: В = В 4+ В 5 – В 2.
Магнитные индукции В 2 и В 4 в точке О создаются лишь половинами кругового тока, поэтому (в соответствии с законом Био-Савара-Лапласа):
 ;
;
 .
.
Магнитную индукцию В 5 найдем, воспользовавшись выражением для магнитной индукции поля, создаваемого отрезком провода с током I:
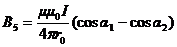 .
.
В нашем случае  ,
,  (
( ),
),  (
(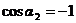 ). Тогда
). Тогда
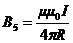 .
.
Используя найденные выражения для В 2, В 4 и В 5, получим
 .
.
 .
.
Произведем вычисления:
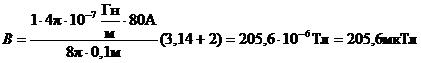
Ответ: В = 205,6 мкТл.
Пример 7. На упругой нити, постоянная кручения которой С = 9,8×10-6 Н×м/рад, подвешена квадратная рамка со стороной а = 3 см, содержащая N = 200 витков тонкого провода. Плоскость рамки совпадает с направлением линии индукции внешнего магнитного поля. Определить индукцию внешнего магнитного поля, если при пропускании по рамке тока I = 1 А она повернулась на угол j = 60°.
| Дано: | Решение: |
| С = 9,8×10-6 Н×м/рад a = 3 см = 0,03 м I = 1 А j = 60° N = 200 | На рамку действуют два вращающих момента сил:  – момент сил, с которым внешнее магнитное поле действует на рамку с током I, и – момент сил, с которым внешнее магнитное поле действует на рамку с током I, и  – момент упругих сил, возникающих при закручивании – момент упругих сил, возникающих при закручивании
|
| В -? |
нити, на которой подвешена рамка. Рамка бу 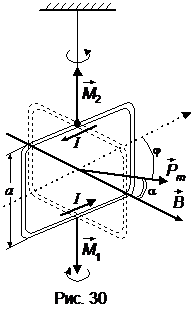 дет находиться в равновесии при выполнении условия:
дет находиться в равновесии при выполнении условия:
 .
.
Направления этих моментов противоположны друг другу, поэтому получим:
 , (1)
, (1)
|
 (Pm – магнитный момент рамки с током, В – индукция магнитного поля, α – угол между нормалью к плоскости рамки и направлением линий индукции магнитного поля, рис. 30);
(Pm – магнитный момент рамки с током, В – индукция магнитного поля, α – угол между нормалью к плоскости рамки и направлением линий индукции магнитного поля, рис. 30);
 (С – постоянная кручения, показывающая величину момента упругой силы, возникающей при повороте рамки на угол, равный единице, j – угол поворота рамки).
(С – постоянная кручения, показывающая величину момента упругой силы, возникающей при повороте рамки на угол, равный единице, j – угол поворота рамки).
Если учесть, что  , где I – сила тока в рамке, S – площадь рамки, а – сторона квадратной рамки, N – число витков рамки; равенство (1) можно переписать в виде:
, где I – сила тока в рамке, S – площадь рамки, а – сторона квадратной рамки, N – число витков рамки; равенство (1) можно переписать в виде:
 ,
,
откуда  (2)
(2)
Из рис. 30 видно, что  , значит,
, значит,  . С учетом этого равенство (2) примет вид:
. С учетом этого равенство (2) примет вид:
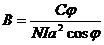 .
.
Подставим числовые значения и произведем вычисления:
 .
.
Ответ: В =11,4×10-5 Тл.
Пример 8. Магнитное поле создано кольцевым проводником радиусом R = 20 см, по которому течет ток I = 100 А. На оси кольца расположено другое кольцо малых размеров с магнитным моментом Pm = 10-2 А×м2. Плоскости колец параллельны, а расстояние между ними х = 1 см. Определить силу, действующую на малое кольцо.
| Дано: | Решение: |
| R = 20 см = 0,2 м I = 100 А Pm = 10-2 А×м2 x = 1 см = 0,01 м | В неоднородном магнитном поле на контур действует сила
 , ,
|
| F -? |
 где
где  – изменение вектора индукции магнитного поля, рассчитанного на единицу длины вдоль направления, совпадающего с вектором
– изменение вектора индукции магнитного поля, рассчитанного на единицу длины вдоль направления, совпадающего с вектором  .
.
Индукция магнитного поля на оси кругового тока
 ,
,
где х – расстояние от центра кольца до точки, в которой определяется магнитная индукция. Тогда


и  .
.
Убедимся в том, что правая часть равенства дает единицу силы (Н):

 .
.
Произведем вычисления:
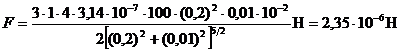 .
.
Ответ: F = 1,35 мкН.
Пример 9. Электрон, влетев в однородное магнитное поле (В = 0,5 Тл), стал двигаться по окружности радиуса R = 8 см. Определить магнитный момент Pm эквивалентного кругового тока.
| Дано: | Решение: |
| В = 0,5 Тл R = 8 см | Движение электрона в однородном магнитном поле будет происходить по окружности только в том случае, когда электрон влетит в магнитное поле перпендикулярно линиям |
| Pm -? |
индукции  . Так как сила Лоренца перпендикулярна вектору скорости
. Так как сила Лоренца перпендикулярна вектору скорости  , то она сообщит электрону центростремительное ускорение
, то она сообщит электрону центростремительное ускорение  .
.
 Пусть линии магнитной индукции
Пусть линии магнитной индукции  перпендикулярны плоскости чертежа и направлены «от нас», тогда направление вектора
перпендикулярны плоскости чертежа и направлены «от нас», тогда направление вектора  и траектория электрона указаны на рисунок 32.
и траектория электрона указаны на рисунок 32.
Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением
 ,
,
где е – заряд электрона;
Т – период его обращения.
Период обращения  ,
,
где 2 pR – длина окружности (путь, проходимый электроном за период Т со скоростью  ).
).
Тогда  .
.
Магнитный момент Pm эквивалентного кругового тока 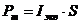 ,
,
Где S – площадь, ограниченная окружностью, описываемой электроном ( ). Следовательно
). Следовательно
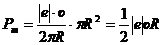 . (*)
. (*)
Так как  , или
, или  , то
, то  . Подставив это выражение в равенство (*), получим
. Подставив это выражение в равенство (*), получим
 ,
,
где е = 1,6×10-19 Кл, m = 9,1×10-31 кг.
Произведем вычисления:


Ответ: Pm = 7,03 пА×м2.
Пример 10. Электрон движется в однородном магнитном поле (В =10 мТл) по винтовой линии, радиус которой R = 1 см и шаг и шаг h = 6 см. Определить период Т обращения электрона и его скорость  .
.
| Дано: | Решение: |
| В = 10 мТл = 10×10-3 Тл R = 1 см = 10-2 м h = 6 см = 6×10-2 м | Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом ( ) к линиям ) к линиям
|
Т -?  -? -?
|
магнитной индукции. Разложим, как показано на рисунке 33, скорость  электрона на две составляющие:
электрона на две составляющие:
 .
.
По модулю  , где
, где  ;
;  .
.
На электрон действует сила Лоренца 
|
Сила Лоренца сообщает электрону нормальное ускорение  . Согласно второму закону Ньютона можно написать
. Согласно второму закону Ньютона можно написать  , или
, или  , откуда
, откуда  . Период обращения электрона связан с составляющей скорости
. Период обращения электрона связан с составляющей скорости  соотношением
соотношением
 .
.
Тогда получим: 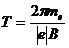 .
.
Произведем вычисления:
 .
.
За время, равное периоду обращения Т, электрон пройдет вдоль силовой линии расстояние, равное шагу винтовой линии, т.е.  , откуда
, откуда
 .
.
Модуль скорости электрона
 .
.
|
|
|


Ответ: Т = 3,57 нс,  = 24,6 Мм/с.
= 24,6 Мм/с.
|
|
| Дано: | Решение: |
| N = 1000 n = 10 с-1 В = 0,04 Тл α = 60° S = 100 см2 = 10-2 м2 | По закону Фарадея-Максвелла:
 .
Потокосцепление .
Потокосцепление  , где N – число витков катушки, пронизываемых магнитным потоком Ф. , где N – число витков катушки, пронизываемых магнитным потоком Ф.
|
| e i -? |
Тогда получим:  .
.
Магнитный поток, пронизывающий катушку в момент времени t, изменяется по закону  , где ω – угловая скорость катушки (
, где ω – угловая скорость катушки ( ).
).
 Мгновенное значение ЭДС индукции:
Мгновенное значение ЭДС индукции:
 .
.
Если учесть, что угол  (рисунок 34), а
(рисунок 34), а  , то получим
, то получим
 .
.
Произведем вычисления:

Ответ: ε i =12,56 В.
Пример 12. Квадратная проволочная рамка со стороной а = 5 см и сопротивлением R = 10 мОм находится в однородном магнитном поле (В = 40 мТл). Нормаль к плоскости рамки составляет угол j = 30° с линиями магнитной индукции. Определить заряд q, который пройдет по рамке, если магнитное поле выключить.
| Дано: | Решение: |
| а = 5 см = 5×10-2 м R = 10 мОм = 10-2 Ом В = 40 мТл = 4×10-2 Тл j = 60° | При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникает ЭДС индукции
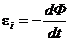
|
Эта ЭДС индукции вызовет в рамке индукционный ток, мгновенное значение которого, согласно закону Ома для полной цепи, равно  , R – сопротивление рамки. Тогда
, R – сопротивление рамки. Тогда  .
.
Так как мгновенное значение силы индукционного тока  , то это выражение можно переписать в виде
, то это выражение можно переписать в виде  , откуда
, откуда
 .
.
Проинтегрировав это выражение, найдем:
 , или
, или  .
.
Заметив, что при выключенном поле (конечное состояние) Ф 2=0, последнее равенство перепишется в виде  .
.
По определению магнитного потока имеем  , где S – площадь рамки. Рамка квадратная, т.е. S = а 2. Тогда
, где S – площадь рамки. Рамка квадратная, т.е. S = а 2. Тогда  и
и
 .
.
Произведем вычисления:
 .
.
Ответ: q = 8,67 мКл.
Пример 13. Плоский квадратный контур со стороной а = 10 см, по которому течет ток I = 100 А, свободно установился в однородном магнитном поле (В = 1 Тл). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) j 1 = 90°; 2) j 2 = 3°. При повороте контура сила тока в нем поддерживается неизменной.
| Дано: | Решение: | ||||
I = 100 А В = 1 Тл j 1= 90° j 2= 3° | На контур с током в магнитном поле действует момент силы (рисунок 35)
 , (1)
где , (1)
где  – магнитный момент контура;
В – магнитная индукция; – магнитный момент контура;
В – магнитная индукция;
| ||||
| А 1-? А 2-? |
|
 j – угол между векторами
j – угол между векторами  и
и  .
.
|
|
 и
и  сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будут стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу работы в дифференциальной форме
сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будут стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу работы в дифференциальной форме  .
.
Учитывая формулу (1), получаем
 .
.
Работа А при повороте на конечный угол j равна
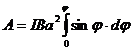 . (2)
. (2)
1. Работа при повороте на угол j 1= 90°
 .
.
Произведем вычисления:
 .
.
2. Работа при повороте на угол j 2= 3°.
В этом случае, учитывая, что угол j 2 мал, заменим в выражении (2)  :
:
 .
.
Выразим угол j 2 в радианах: j 2 = 3° = 0,0523 рад. Тогда

 .
.
Ответ: А 1 = 1 Дж; А 2 = 1,37 мДж.
Пример 14. По соленоиду течет ток I = 5 А. Длина соленоида l = 1 м, число витков N = 500. В соленоид вставлен железный сердечник. Найти намагниченность j и объемную плотность энергии магнитного поля w соленоида.
| Дано: | Решение: |
| I = 5 А L = 1 м N = 500 | Намагниченность определяется отношением магнитного момента к объему магнетика и связана с напряжённостью магнитного поля соотношением  , где χ – магнитная восприимчивость среды. , где χ – магнитная восприимчивость среды.
|
| j -? w-? |
Поле соленоида можно считать однородным. В этом случае напряжённость поля вычисляется по формуле  ,
,
где  – число витков, приходящихся на единицу длины соленоида.
– число витков, приходящихся на единицу длины соленоида.
Связь между магнитной восприимчивостью χ и магнитной проницаемостью μ среды выражается формулой  .
.
Используя соотношение  , находим
, находим 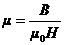 .
.
Тогда получим:  ;
;
 . (*)
. (*)
Определим напряженность магнитного поля соленоида
 .
.
По графику на рис. 36 находим, что напряжённости Н = 2500 А/м соответствует индукция магнитного поля В = 1,45 Тл.
Подставим в формулу (*) значения физических величин и произведём вычисления:
 .
.
Объемная плотность энергии магнитного поля соленоида вычисляется по формуле
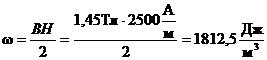 .
.
Ответ: j = 11,52 А/м; ω = 1812,5 Дж/м3.

К о н т р о л ь н а я р а б о т а № 3
| Вар. | Номера задач | |||||||
301. Бесконечно длинный провод изогнут так, как это показано на рис. 37. Радиус дуги окружности R =10 см. Определите магнитную индукцию  поля, создаваемого в точке О током I =50 А, текущим по этому проводу.
поля, создаваемого в точке О током I =50 А, текущим по этому проводу.
302. Магнитный момент  тонкого проводящего кольца
тонкого проводящего кольца 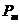 =5 А×м2. Определите магнитную индукцию
=5 А×м2. Определите магнитную индукцию  в точке А, находящейся на оси кольца и удаленной от точек кольца на расстояние r =20 см (рисунок 38).
в точке А, находящейся на оси кольца и удаленной от точек кольца на расстояние r =20 см (рисунок 38).
303. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I 1=100 А и I 2=200 А. Определите магнитную индукцию  в точке А (рисунок 39). Расстояние d =10 см.
в точке А (рисунок 39). Расстояние d =10 см.
304. По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи I 1=100 А и I 2=200 А. Определите магнитную индукцию  в точке А, равноудаленной от проводов на расстояние d =20 см (рисунок 40).
в точке А, равноудаленной от проводов на расстояние d =20 см (рисунок 40).
305. По бесконечно длинному проводу, изогнутому так, как показано на рисунке 41, течет ток I =200 А. Определите магнитную индукцию В в точке О. Радиус дуги R =15 см.
|

306. По бесконечно длинному проводу, изогнутому так, как показано на рисунке 42, течёт ток I =150 А. Определите магнитную индукцию  в точке О. Радиус дуги R =20 см.
в точке О. Радиус дуги R =20 см.
Не нашли, что искали? Воспользуйтесь поиском: