Основные законы и формулы. · Первый постулат Бора. Электрон в атоме водорода движется, не излучая, по круговой орбите, для которой момент импульса электрона

· Первый постулат Бора. Электрон в атоме водорода движется, не излучая, по круговой орбите, для которой момент импульса электрона

, или ,

где m_e – масса электрона;

– скорость электрона на n -ой орбите;

r_n – радиус n -ой стационарной орбиты;

ħ = 1,05×10^-34 Дж×с, или h = 6,63×10^-34 Дж×с – постоянная Планка;

n = 1, 2, 3,… – квантовое число (номер орбиты электрона).

· Второй постулат Бора. При переходе электрона с одной орбиты на другую атом водорода излучает или поглощает квант энергии:

,

где 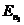и 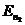– полные энергии электрона в атоме на соответствующей орбите.

· Полная энергия электрона в атоме водорода

(n = 1, 2, 3,…),

где n – номер орбиты;

m_e – масса электрона;

е – заряд электрона;

ε₀ = 8,85×10^-12 Ф/м – электрическая постоянная;

h – постоянная Планка.

· Формула, позволяющая найти частоты v или длины волн λ, соответствующие линиям водородного спектра (сериальная формула Бальмера)

,

где R – постоянная Ридберга (R = 1,10×10⁷ м^-1);

с – скорость света в вакууме;

n₁ и n₂ – квантовые числа, определяющие номера орбит электрона.

Для водородоподобных ионов формула имеет вид:

,

где Z – порядковый номер в таблице Менделеева.

· Длина волны де Бройля

,

где p=m – модуль импульса движущейся частицы.

· Импульс частицы и его связь с кинетической энергией T:

а) ; ;

б) ; ,

где m ₀ – масса покоя частицы;

m – релятивистская масса частицы;

– скорость частицы;

с – скорость света в вакууме;

Е ₀ – энергия покоя частицы (Е ₀ = m ₀ с²).

· Соотношение неопределенностей:

а) для координаты и импульса

,

где D Р_х – неопределенность проекции импульса на ось Х;

D х – неопределенность координаты;

б) для энергии и времени

,

где D Е – неопределенность энергии;

D t – неопределенность времени жизни квантовой системы в данном энергетическом состоянии.

· Одномерное уравнение Шредингера для стационарных состояний

,

где ψ(х) – волновая функция, описывающая состояние частицы;

m – масса частицы;

Е – полная энергия частицы;

U = U(х) – потенциальная энергия частицы.

· Плотность вероятности

,

где d ω(x) – вероятность того, что частица может быть обнаружена вблизи точки с координатой x на участке dx.

· Вероятность обнаружения частицы в интервале от х ₁ до х ₂

· Решение уравнение Шредингера для одномерного бесконечно глубокого, прямоугольного потенциального ящика:

а) 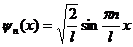– собственная нормированная волновая функция;

б) 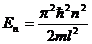– собственное значение энергии, где n – квантовое число (n = 1, 2, 3,…); l – ширина ящика.

В области 0 £ x £ l U = ∞ и ψ (х) = 0.

· Коэффициент прозрачности прямоугольного потенциального барьера, т.е. вероятность прохождения (туннелирования) микрочастицы сквозь барьер:

,

где D ₀ – коэффициент, по порядку величины близкий к единице;

U – высота потенциального барьера;

l – его ширина;

Е – энергия частицы;

m – масса частицы.

· Закон радиоактивного распада

dN = – λ × N × dt, или ,

где dN – число ядер, распадающихся за интервал времени dt;

N – число ядер, не распавшихся к моменту времени t;

N ₀ – число ядер в начальный момент (t = 0);

λ – постоянная радиоактивного распада.

· Число ядер, распавшихся за время t:

.

· Период полураспада

.

· Среднее время жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшилось в е раз:

.

· Число атомов, содержащихся в радиоактивном изотопе

,

где m – масса изотопа;

М – молярная масса;

N_A – постоянная Авогадро (N_A =6,02×10²³ моль^-1).

· Активность радиоактивного изотопа

, или ,

где dN – число ядер, распадающихся за интервал времени dt;

А ₀ – активность изотопа в начальный момент времени (t = 0), А ₀ =λN ₀.

· Удельная активность изотопа

.

· Дефект массы ядра

,

где Z – зарядовое число (число протонов в ядре);

А – массовое число (число нуклонов в ядре);

(А-Ζ) – число нейтронов в ядре;

m_р – масса протона;

m_n – масса нейтрона;

m_я – масса ядра.

· Энергия связи ядра

Е_св = D mс²,

где Δ m – дефект массы ядра;

с – скорость света в вакууме.

Во внесистемных единицах энергия связи ядра равна Е_св = 931×Δ m Мэв, где дефект массы Δ m – в а.е.м.; 931 – коэффициент пропорциональности (1 а.е.м. ~ 931 МэВ).

· Правило смещения:

1) для α -распада: ;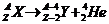

2) для β^- -распада: ;

3) для β⁺ -распада: .

· Ядерные реакции. Символическая запись ядерной реакции может быть дана или в развернутом виде, например:

или сокращенно

.

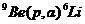При сокращенной записи порядковый номер атома не пишут, так как он определяется химическим символом атома. В скобках на первом месте ставят обозначение бомбардирующей частицы, на втором – обозначение частицы, вылетающей из составного ядра, и за скобками – химический символ ядра-продукта.

Обозначения частиц: р – протон, n – нейрон, d – дейтрон, t – тритий (тритон), α -альфа-частица, γ-гамма-фотон.

· Энергетический эффект ядерной реакции

Q = c ²[(m ₁ +m ₂) –(m ₃ +m ₄)],

где m ₁ – масса покоя ядра-мишени;

m ₂ – масса покоя бомбардирующей частицы,

(m ₃ + m ₄) – сумма масс покоя ядер продуктов реакции.

Если m ₁ + m ₂ > m ₃ + m ₄, то энергия освобождается, реакция экзотермическая. Если m ₁ + m ₂ < m ₃ + m ₄, то энергия поглощается, реакция эндотермическая.

· При решении задач на ядерные реакции применяются законы сохранения:

1) электрического заряда: z ₁ + z ₂ = z ₃ + z ₄;

2) суммарного числа нуклонов: А ₁ + А ₂ = А ₃ + А ₄;

3) релятивистской полной энергии: Е ₁ + Е ₂ = Е ₃ + Е ₄; или

,

где – сумма энергий покоя частиц и их кинетических энергий до реакции; справа то же для частиц после реакции;

4) импульса: р ₁ + р ₂ = р ₃ + р ₄.

Не нашли, что искали? Воспользуйтесь поиском: