Примеры решения задач. Пример 1. Определить для серной кислоты:

Пример 1. Определить для серной кислоты:

1) относительную молекулярную массу M_r;

2) молярную массу М.

Решение.

1. Относительная молекулярная масса вещества определяется по формуле ,

где n_i – число атомов i -го элемента, входящих в молекулу;

А_r,i – относительная атомная масса i -го элемента.

Химическая формула серной кислоты имеет вид H₂SO₄. Следовательно, M_r=n₁A_r,1+n₂A_r,2+n₃A_r,3.

Из формулы серной кислоты следует, что n₁ =2 (два атома водорода), n₂ =1 (один атом серы) и n₃ =4 (четыре атома кислорода). Значения относительных атомных масс водорода, серы и кислорода находим в таблице Д. И. Менделеева: A_r,1 =1; A_r,2 =32; A_r,3 =16.

Тогда получим: M_r =2×1+1×32+4×16=98.

2. Молярную массу серной кислоты находим по формуле:

M=M_r ×10^-3 кг/моль.

Следовательно, M =98×10^-3 кг/моль.

Пример 2. В баллоне объемом 10 л находится гелий под давлением p₁ =1 MПа и при температуре Т₁ =300 К. После того, как из баллона было взято m =10 г гелия, температура в баллоне понизилась до T₂ =290 К. Определить давление p₂ гелия, оставшегося в баллоне.

Дано:	Решение:
V =10 л = 10-2 м3 p1 =1МПа=106Па T1 =300К m =10г=10-2кг Т2 =290К	Запишем уравнение Менделеева-Клапейрона для конечного состояния газа: 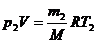, (1) где m2 – масса гелия в баллоне в конечном состоянии;

М – молярная масса гелия (M =4×10^-3 кг/моль);

R – молярная газовая постоянная (R =8,31 Дж/моль×К).

Искомое давление:

. (2)

Массу m₂ гелия выразим через массу m₁, соответствующую начальному состоянию, и массу m гелия, взятого из баллона: m₂=m₁-m.

Из уравнения Менделеева-Клапейрона для начального состояния получаем: 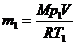. Тогда .

Подставив это выражение в уравнение (2), найдем:

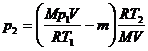, или .

Произведем вычисления:

Ответ: p₂ =0,364 МПа.

Пример 3. Найти среднюю кинетическую энергию <e _вр > вращательного движения одной молекулы кислорода при температуре Т =350 К, а также кинетическую энергию Е_к вращательного движения всех молекул кислорода массой m =4 г.

Дано:	Решение:
Т =350 К m =4 г=4×10-3 кг	На каждую степень свободы молекулы газа приходится одинаковая средняя энергия ,
<e вр >-? Ек -?

где k – постоянная Больцмана;

Т – термодинамическая температура газа.

Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода

. (1)

Кинетическая энергия вращательного движения всех молекул газа

E_к =<e _вр >× N. (2)

Число всех молекул газа

N=N_A×n =N_A × , (3)

где N_A – постоянная Авогадро;

n – количество вещества;

m – масса газа;

М – молярная масса газа.

Подставив выражение (3) в формулу (2), получаем:

. (4)

Произведем вычисления, учитывая, что для кислорода М =32×10^-3 кг/моль; k =1,38×10^-23 Дж/К; N_A =6,02×10²³ моль^-1:

<e>=1,38×10^-23×350 Дж = 4,83×10^-21 Дж,

Ответ: <e _вр >=4.83×10^-21 Дж; Е_к =364 Дж.

Пример 4. Кислород массой m =2 кг занимает объем V₁ =1 м³ и находится под давлением p₁ =0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂ =3 м³, а затем при постоянном объеме до давления p₃ =0,5 МПа. Найти изменение D U внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

Дано:	Решение:
m =2 кг V1 =1 м3 p1 =0,2 МПа=2×105 Па p1 =const V2 =3 м3 V2 =const p3 =0,5 МПа=5×105 Па	Изменение внутренней энергии газа , где i – число степеней молекулы газа (для двухатомных молекул кислорода i =5); D T=T 3– T 1 – разность температур газа в конечном (третьем) и начальном состояниях.
D U -? A -? Q -? p(V) -?

Начальную и конечную температуру газа найдем из уравнения Менделеева-Клапейрона :

и .

Тогда

.

Произведем вычисления:

.

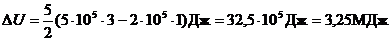Работа расширения газа при постоянном давлении (p ₁=const) выражается формулой A ₁ =p ₁×D V=p ₁(V ₂– V ₁). Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. А₂ =0. Следовательно, полная работа, совершенная газом:

А=А ₁ +А ₂ =А ₁ =p ₁(V ₂– V ₁).

Произведем вычисления:

A =2×10⁵×(3-1) Дж = 4×10⁵ Дж.

Согласно первому закону термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии DU и работы A: Q =D U + A. Следовательно,

Q =32,5×10⁵ Дж + 4×10⁵ Дж =

=36,5×10⁵ Дж =3,65 МДж.

График процесса приведен на рисунке 11.

Пример 5. В цилиндре под поршнем находится водород массой m =0,02 кг при температуре T₁ =300 К. Водород сначала расширился адиабатно, увеличив свой объем в n₁ =5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n₂ =5 раз. Найти температуру в конце адиабатного расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.

Дано:	Решение:
M =0,02 кг Т1 =300 К n1 =5 n2 =5	Температуры и объемы газа, совершающего адиабатический процесс, связаны между собой соотношением , (1)
T 2-? A 1-? A 2-?

где g – показатель адиабаты, ;

i – число степеней свободы молекулы.

Для водорода как двухатомного газа i =5. Следовательно, . Так как , то , откуда

. (2)

Работа А₁ газа при адиабатическом расширении может быть определена по формуле:

, (3)

где С_V – молярная теплоемкость газа при постоянном объеме;

М – молярная масса газа.

Работа А ₂ при изотермическом процессе может быть выражена в виде:

, или , (4)

где .

Подставляя числовые значения величин в выражения (2), (3) и (4), произведем вычисления, учитывая, что для водорода М =2×10^-3 кг/моль.

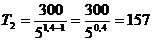К.

(5^0,4= x; или lg x =0,4lg5=0,2796, тогда x =1,91; 5^0,4=1,91)

.

Пример 6. Температура нагревателя тепловой машины 500 К. Температура холодильника 400 К. Определить КПД тепловой машины, работающей по циклу Карно, и полную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты.

Дано:	Решение:
Tн =500 К Тх =400 К Qн =1675 Дж t =1 c	КПД машины, работающей по циклу Карно, определяется по формуле , (1)
h-? N -?

или . (2)

Полная мощность машины

, (3)

или . (4)

Подставляя числовые значения в выражения (1) и (4), получим:

; h=20%.

.

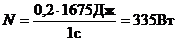Ответ: h=20%; N =335 Вт.

Пример 7. Найти изменение энтропии при переходе 8 г кислорода от объема 10 л при температуре 80°С к объему 40 л при температуре 300^оС.

Дано:	Решение:
m =8 г=8×10-3 кг V1 =10 л=10-2 м3 T1 =353 К V2 =40 л=4×10-2 м3 T2 =573 К	Изменение энтропии: 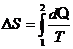. Согласно первому закону термодинамики d Q = dU + dA

где 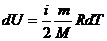– изменение внутренней энергии газа;

dA = p × dV – работа газа при изменении объема.

Из уравнения Менделеева-Клапейрона находим давление газа . Тогда , а .

Следовательно

,

или .

Произведем вычисления, учитывая, что для кислорода i =5; М =32×10^-3 кг/моль.

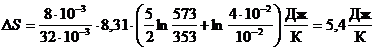
Ответ: D S = 5,4 Дж/К.

К о н т р о л ь н а я р а б о т а № 1

101. Тело брошено вертикально вверх с начальной скоростью _o=4м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью _о вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

102. Двое играют в мяч, бросая его друг другу. Какой наибольшей высоты h_m достигнет мяч во время игры, если он от одного игрока к другому летит t =2 с?

103. Тело брошено под углом a=30° к горизонту со скоростью _о=30 м/с. Каковы будут нормальное а_n и тангенциальное a _t ускорения тела через время t =1 с после начала движения? Сопротивление воздуха не учитывать.

104. Материальная точка движения по окружности с постоянной угловой скоростью w= рад/с. Во сколько раз путь D S, пройденный точкой за время t =4 с, будет больше модуля ее перемещения D r? Принять, что в момент начала отсчета времени радиус-вектор , задающий положение точки на окружности, относительно исходного положения, был повернут на угол j_o = рад.

105. Тело массой 2 кг движется прямолинейно со скоростью, зависимость которой от времени выражается уравнением =6 t²+ 10 t. Определить путь, пройденный телом за 5 секунд, и силу, действующую на тело в конце пятой секунды.

106. Под действием постоянной силы F =10 H тело движется прямолинейно и зависимость пройденного пути от времени имеет вид S =10-5 t + t². Найти массу тела и импульс тела в конце шестой секунды.

107. Колесо вращается с постоянным угловым ускорением e=2 рад/с. Через t =0,5 с после начала движения полное ускорение колеса стало равно a =13,6 см/с². Найти радиус колеса.

108. Тело брошено со скоростью _о=10 м/с под углом a=45° к горизонту. Найти радиус R кривизны траектории тела через t =1 с после начала движения. Сопротивление воздуха не учитывать.

109. Определить начальную скорость _о, с которой тело брошено вертикально вверх, если точку, находящуюся на высоте h =60 м, оно проходило два раза с промежутком времени D t =4 с. Сопротивление воздуха не учитывать.

110. Диск радиусом R =0,2 м вращается согласно уравнению j=A+Bt+Ct³, где A =3 рад, B= –1 рад/с, C=0,1 рад/с³. Определить тангенциальное а _t , нормальное а_n и полное a ускорения точек на окружности диска для момента времени t =10 с.

111. Определить импульс , полученный стенкой при ударе о нее шарика массой m =300 г, если шарик двигался со скоростью =90 м/с под углом a=60° к плоскости стенки. Удар о стенку считать упругим.

112. С тележки, свободно движущейся по горизонтальному пути со скоростью ₁ =3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной u₁ =4 м/с. Определить горизонтальную составляющую скорости человека при прыжке относительно тележки. Масса тележки m₁ =210 кг, масса человека m₂ =70 кг.

113. Конькобежец, стоя на коньках на льду, бросает камень массой m₁ =2,5 кг под углом a=30° к горизонту со скоростью =10 м/с. Какова будет начальная скорость _о движения конькобежца, если масса его m₂ =60 кг? Перемещением конькобежца во время броска пренебречь.

114. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m₁ =60 кг, масса доски m₂ =20 кг. С какой скоростью u (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) =1 м/с? Массой колес и трением пренебречь.

115. На сколько переместится относительно берега лодка длиной l =3,5 м и массой m₁ =200 кг, если стоящий на корме человек массой m₂ =80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.

116. Лодка длиной l =3 м и массой m =120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m₁ =60 кг и m₂ =90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

117. Плот массой m₁ =150 кг и длиной l =2 м плавает на воде. На плоту находится человек, масса которого m₂ =80 кг. С какой наименьшей скоростью 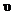и под каким углом a к плоскости горизонта должен прыгнуть человек вдоль плота, чтобы попасть на его противоположный край?

118. Молекула массой m =4,65×10^-26 кг, летящая со скоростью =600 м/с, ударяется о стенку сосуда под углом 60° к нормали и под таким же углом упруго отскакивает от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара.

119. На железнодорожной платформе, движущейся по инерции со скоростью _o=3 км/ч, укреплено орудие. Масса платформы с орудием M =10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m =10 кг вылетает из ствола под углом a=60° к горизонту. Определить скорость снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в n =2 раза.

120. На железнодорожной платформе установлено орудие. Масса платформы с орудием M =15 т. Орудие стреляет вверх под углом j =60° к горизонту в направлении пути. С какой скоростью ₁ покатится платформа вследствие отдачи, если масса снаряда m =20 кг и он вылетает со скоростью ₂=600 м/с?

121. На краю платформы в виде диска диаметром D =2 м, вращающейся по инерции вокруг вертикальной оси с частотой n₁ =8 мин^-1, стоит человек массой m₁ =70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n₂ =10 мин^-1. Определить массу m₂ платформы. Момент инерции человека рассчитывать как для материальной точки.

122. На краю неподвижной скамьи Жуковского диаметром D =0,8 м и массой m₁ =6 кг стоит человек массой m₂ =60 кг. С какой угловой скоростью w начнет вращаться скамья, если человек поймает летящий на него мяч массой m =0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r = 0,4 м от оси скамьи. Скорость мяча =5 м/с.

123. Человек стоит на скамье Жуковского и держит в руках стержень вертикально вдоль оси вращения скамьи. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамейка неподвижна, колесо вращается с частотой n =15 c^-1. С какой угловой скоростью w₂ будет вращаться скамья, если человек повернет стержень на угол j =180° и колесо окажется на нижнем конце стержня? Суммарный момент инерции человека и скамьи I =8 кг×м², радиус колеса R =25 см. Массу колеса m =2,5 кг можно считать равномерно распределенной по ободу. Считать, что центр тяжести человека с колесом находится на оси платформы.

124. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси вращения скамьи. Скамья с человеком вращается с угловой скоростью w₁=4 рад/с. С какой угловой скоростью w₂ будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи I =5 кг×м². Длина стержня l =1,8 м, его масса m =6 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.

125. Платформа в виде диска диаметром D =3 м и массой m₁ =180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью w будет вращаться эта платформа, если по ее краю пойдет человек массой m₂ =70 кг со скоростью =1,8 м/с относительно платформы?

126. Платформа, имеющая форму диска, вращается около вертикальной оси с частотой n₁ = 10 мин-1. На краю платформы стоит человек. С какой частотой n₂ будет вращаться платформа, если человек перейдет к ее центру? Масса платформы m₁ =280 кг, масса человека m₂=80 кг. Платформу считать круглым однородным диском, а человека – точечной массой.

127. Горизонтальная платформа массой m₁ =150 кг вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n = 8 мин ^-1. Человек массой m₂ =70 кг стоит при этом на краю платформы. С какой угловой скоростью w начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека – материальной точкой.

128. Однородный стержень длиной l =1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m =7 г, летящая перпендикулярно стержню и его оси. Определить массу M стержня, если в результате попадания пули он отклонится на угол α=60°. Принять скорость пули =360 м/с.

129. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции с частотой n₁ =0,5 с^-1. Момент инерции тела человека относительно оси вращения I =1,6 кгּм². В вытянутых в стороны руках человек держит две гири массой m =2 кг каждая. Расстояние между гирями l₁ =1,6 м. Сколько оборотов в секунду будет делать скамья с человеком, если он опустит руки и расстояние l₂ между гирями станет равным 0,4 м? Моментом инерции скамейки пренебречь.

130. Горизонтальная платформа массой m =25 кг и радиусом R =0.8 м вращается с частотой n₁ =18 мин ^-1 В центре платформы стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от I₁ =3,5 кгּм² до I₂ = 1 кгּм².

131. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на l_o =3 мм. На сколько сожмется пружина, если этот же груз упадет на верхний конец пружины с высоты h =9 см?

132. Молот массой m₁ =5 кг ударяет небольшой кусок железа, лежащий на наковальне. Масса наковальни m₂ =100 кг. Массой куска железа можно пренебречь. Удар абсолютно неупругий. Определить КПД удара.

133. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия шара T =14 Дж. Определить кинетическую энергию поступательного и вращательного движения.

134. Пуля массой m =10 г летит со скоростью =800 м/с, вращаясь около продольной оси с угловой скоростью ω=3000 об/с. Принимая пулю за цилиндрик диаметром d =8 мм, определить полную кинетическую энергию Т пули.

135. На скамье Жуковского сидит человек и держит в вытянутых руках гири по 10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l₁ =50 см. Скамья вращается с частотой n₁ =1 с^-1. Как изменится частота вращения скамьи и какую работу произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l ₂= 20 см? Суммарный момент инерции человека и скамьи относительно оси вращения I _o=2,5 кг×м². Ось вращения проходит через центр масс человека и скамьи.

136. Маятник в виде однородного шара, жестко скрепленного с тонким стержнем, длина которого равна радиусу шара, может качаться вокруг горизонтальной оси, проходящей через конец стержня. В шар нормально к его поверхности ударилась пуля массой m =10 г, летевшая горизонтально со скоростью =800 м/с, и застряла в шаре. Масса шара M =10 кг, его радиус R =15 см. На какой угол a отклонится маятник в результате удара пули? Массой стержня пренебречь.

137. Сплошной однородный диск катится по горизонтальной плоскости со скоростью =10 м/с. Какое расстояние S пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска μ=0,02.

138. Маховик массой m =4 кг свободно вращается с частотой n =720 мин ^-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика считать равномерно распределенной по его ободу радиусом R =40 см. Через t =30 с под действием тормозящего момента маятник остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

139. Маховик в виде диска массой m =50 кг и радиусом R= 20 см был раскручен до угловой скорости ω₁=480 об/мин и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент М сил трения, считая его постоянным, если до полной остановки маховик сделал N =200 оборотов.

140. Тело массой m =0,5 кг бросают вертикально вверх со скоростью _o=20 м/c. В момент падения на землю скорость тела равна 16 м/с. Определить силу сопротивления воздуха и время движения тела. В течение всего времени движения силу сопротивления воздуха считать постоянной.

141. Ракета, летевшая над поверхностью Земли на высоте h =230 км, в результате кратковременного действия мощной тормозной установки останавливается. С какой скоростью упадет ракета на Землю? Сопротивлением воздуха пренебречь. Считать известными ускорение свободного падения у поверхности Земли и ее радиус.

142. Из бесконечности на поверхность Земли падает метеорит массой m =30 кг. Определить работу А сил гравитационного поля Земли при этом. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

143. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от центра Земли до центра Луны равно 3,84·10⁸ м?

144. На каком расстоянии от центра Земли должно находиться тело, чтобы силы его притяжения к Земле и Луне взаимно уравновешивались? Считать, что масса М Земли больше массы m Луны в 81 раз, а расстояние между их центрами равно 60 радиусам Земли.

145. Определить значение потенциала φ и напряженность σ гравитационного поля на поверхности Земли и Солнца.

146. Вычислить значение первой (круговой) и второй (параболической) космических скоростей вблизи поверхности Луны.

147. С поверхности Земли вертикально вверх пущена ракета со скоростью =5 км/c. На какую высоту она поднимется?

148. Определить радиус R планеты, у которой на экваторе вес тела на h=20% меньше чем на полюсе. Масса планеты М =6·10²⁴ кг, сутки на ней составляют Т =24 часа.

149. Радиус малой планеты r =100 км, средняя плотность вещества планеты ρ =3000 кг/м³. Определить параболическую (вторую космическую) скорость у поверхности этой планеты.

150. Искусственный спутник, используемый в системе телесвязи, запущен в плоскости земного экватора так, что все время находится в зените одной и той же точки Земли. Во сколько раз радиус орбиты спутника больше радиуса Земли R₃ =6370 км?

151. Тело массой m =0,02 кг совершает гармонические колебания с амплитудой А =0,05 м и частотой n = 10 c^-1, начальная фаза колебания равна нулю. Определить полную энергию колеблющегося тела и максимальную силу, действующую на тело. Написать уравнение гармонического колебания.

152. Шарик массой m =60 г колеблется с периодом Т =2 с. В начальный момент времени смещение шарика x_o =8 см и он обладает энергией Е =0,02 Дж. Записать уравнение простого гармонического колебания шарика.

153. По условию задачи 152 определить возвращающую силу, действующую на шарик в момент времени t =5 с после начала колебания.

154. Материальная точка массой m =5 г совершает гармонические колебания с частотой n=0,5 c^-1. Амплитуда колебаний А =0,03 м. Определить скорость точки в момент, когда смещение ее равно х =1,5 см.

155. Определить частоту простых гармонических колебаний обруча радиусом R =50 см около горизонтальной оси, проходящей через образующую обруча.

156. Материальная точка совершает простые гармонические колебаний так, что в начальный момент времени смещение x_o =4 см, а скорость _o=10 см/c. Определить амплитуду А и начальную фазу φ _o колебаний, если их период Т =2 с.

157. На стержне длиной l =50 см укреплены два одинаковых шарика: один на конце стержня, другой – в середине стержня. Стержень с шариками совершает колебания около горизонтальной оси, проходящей через свободный конец стержня. Определить период колебаний стержня. Массой стержня пренебречь.

158. На гладком горизонтальном столе лежит шар массой M =200 г, прикрепленный к горизонтально расположенной пружине с жесткостью k =500 H/м. В шар попадает пуля массой m =10 г, летящая со скоростью =300 м/c, и застревает в нем. Пренебрегая массой пружины и сопротивлением воздуха, определить амплитуду А и период колебаний Т шара.

159. Математический маятник длиной l₁ =20 см и физический маятник в виде тонкого прямого стержня длиной l₂ =30 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние a центра тяжести стержня от оси колебаний.

160. Тонкий однородный стержень длиной l =40 см свободно вращается вокруг горизонтальной оси, отстоящей на расстоянии a =12 см от его середины. Определить частоту n колебаний стержня относительно этой оси.

161. В баллоне емкостью V =15 л находится смесь, содержащая m₁ =10 г водорода, m₂ =54 г водяного пара и m₃ =60 г окиси углерода. Определить давление смеси газов в баллоне при температуре t =27°С.

162. При давлении p =705 кПа и температуре t =26°С плотность некоторого газа ρ =12,5 кг/м³. Определить относительную молекулярную массу Mr газа.

163. В баллоне находится газ при температуре T₁ =350 К. До какой температуры T₂ надо нагреть газ, чтобы его давление увеличилось в 1,5 раза?

164. В сосуде объемом V =2 м³ находится смесь m₁ =4 кг гелия и m₂ =2кг водорода при температуре t =27°С. Определить давление и молярную массу смеси газов.

165. В пустой сосуд, объем которого V =5 л, впустили V₁ =3 дм³ азота под давлением p₁ =250 кПа и V₂ =4 дм³ водорода под давлением p₂ =50кПа. Найти давление образовавшейся смеси.

166. Сколько молекул водорода находится в сосуде емкостью V =2 л, если средняя квадратичная скорость движения молекул < 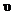_кв >=500 м/c, а давление на стенки сосуда p =10³ Па?

167. В сосуде емкостью V= 200 см³ находится газ при температуре t =47°С. Из-за утечки газа из сосуда просочилось N =10²¹

молекул. На сколько снизилось давление газа в сосуде?

168. В сосуде емкостью V =10 л находится m =2 г кислорода. Определить среднюю длину свободного пробега молекул. Диаметр молекулы кислорода d =0,27 нм.

169. Средняя длина свободного пробега молекулы азота при некоторых условиях <l> =2 см. Найти плотность ρ азота при этих условиях. Эффективный диаметр молекул азота принять равным 0,38 нм.

170. Вычислить удельные теплоемкости с_V и с_P газа, зная, что его молярная масса М =4×10^-3 кг/моль и показатель адиабаты γ=1,67.

171. Найти кинетическую энергию Е_к вращательного движения всех молекул кислорода массой m =5 г при температуре t =65°C.

172. Смесь двух газов состоит из гелия массой m₁ =5 г и водорода массой m₂ =2 г. Найти отношение молярных теплоемкостей этой смеси.

173. В сосуде объемом V =10 л находится одноатомный газ при нормальных условиях. Определить теплоемкость C_V этого газа при постоянном объеме.

174. Углекислый газ при температуре t =40°С и под давлением p =350 кПа занимает объем V =10 л. Определить теплоемкость C_P этого газа при постоянном давлении.

175. Идеальный газ при давлении p =0,4 МПа и температуре Т =350 К занимает объем V =300 л. Определить показатель адиабаты g идеального газа, если теплоемкость этого газа при постоянном объеме С_V =857 Дж/К.

176. Определить суммарную кинетическую энергию Е_к поступательного движения всех молекул гелия при температуре Т =120 К, содержащихся в количестве вещества ν =1,5 моля.

177. Молярная внутренняя энергия кислорода U _μ=6,02 кДж/моль. Определить среднюю кинетическую энергию <ε _вр > вращательного движения одной молекулы кислорода.

178. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию <ε> одной молекулы этого газа при температуре Т =300 К, если количество вещества водорода ν =0,5 моль.

179. Определить удельные теплоемкости с_V и с_P газа, если известно, что при нормальных условиях его удельный объем V =0,7 м³/кг. Какой это газ?

180. Водород массой m =20 г находится при температуре t =37°С. Найти: 1) среднюю кинетическую энергию <e> одной молекулы водорода; 2) среднюю кинетическую энергию < E_вр > вращательного движения всех молекул водорода. Газ считать идеальным.

181. Найти работу и изменение внутренней энергии при адиабатном расширении m =1 кг воздуха, если его объем увеличился в n =10 раз. Начальная температура воздуха t =15°С.

182. В закрытом сосуде находится смесь азота массой m₁ =56 г и кислорода массой m₂= 64 г. Определить изменение внутренней энергии смеси, если ее охладили на D t =20°С.

183. Во сколько раз увеличится объем v =1 моля водорода при изотермическом расширении при температуре t= 27°С, если при этом была затрачена теплота Q =4 кДж?

184. Водород, занимающий объем V₁ =5 ли находящийсяпод давлением P₁= 10⁵ Па, адиабатно сжат до объема V₂ =1 л. Найти работу сжатия и изменение внутренней энергииводорода.

185. Определить количество теплоты Q, которое надо сообщить кислороду объемом V =50 л при его изохорном нагревании, чтобы давление газа повысилось на D p =0,5 МПа.

186. При изотермическом расширении азота при температуре T =280К объем его увеличился в n =2 раза. Определить: 1) совершенную при расширении газа работу A; 2) изменение внутренней энергии D U; 3) количество теплоты Q, полученное газом. Масса азота m =0,2 кг.

187. Определить работу A, которую совершит азот, если ему при постоянном давлении сообщить количество теплоты Q = 21 кДж. Найти также изменение D U внутренней энергии газа.

188. Определить работу, совершенную кислородом в результате изобарического расширения, если при этом затрачена теплота Q = 35 кДж.

189. В результате изобарического процесса при давлении p =2 МПа водород массой m =280 г совершил работу A =1,43 кДж. Определить конечный объем газа, если начальная температура водорода T₁ = 290 К.

190. Азот объемом V₁ =5 л находится под давлением 1 МПа. Определить, какое количество теплоты Q необходимо сообщить газу, чтобы увеличить его давление вдвое в результате изохорного процесса.

191. Под давлением p₁ =3 МПа находится кислород объемом V₁ =2 л. Найти, какое количество теплоты необходимо сообщить газу, чтобы увеличить его объем в два раза в результате изобарического процесса.

192. Азот массой m =200 г и температурой T₁ =250 К был адиабатически сжат. При этом была совершена работа A =30 кДж. Определить конечную температуру T₂ газа.

193. Совершая прямой цикл Карно, газ отдал холодильнику 0,25 теплоты, полученной от нагревателя. Определить температуру Т_х холодильника, если температура нагревателя T_н =500 К.

194. Определить работу А₁ изотермического расширения газа, совершающего цикл Карно, КПД которого h= 0,4, если работа изотермического сжатия А₂ =4,8 Дж.

195. Водород массой m =10 г изобарно расширяется, при этом его объем увеличивается в 2 раза. Определить изменение энтропии водорода при этом процессе.

196. Определить изменение энтропии при изобарном нагревании азота массой m =0,1 кг от температуры t ₁=17°С до t ₂=100°С.

197. Определить изменение энтропии при изохорическом нагревании двухатомного газа в количестве n =2 моля, если при этом его термодинамическая температура увеличилась в n =2 раза.

198. Определить изменение энтропии свинца массой m =4 кг при охлаждении его от t ₁=327°С до t ₂=0°С. (C_уд.св. =126 Дж/кгК)

199. При изобарическом нагревании кислорода массой 1 кг его температура увеличилась в n =3 раза. Определить изменение энтропии при этом процессе.

200. Объем гелия, масса которого m =2 кг, увеличился в n =5 раз при изотермическом нагревании. Найти изменение энтропии в этом случае.

ЭЛЕКТРОСТАТИКА

Не нашли, что искали? Воспользуйтесь поиском: