Сведения о приближенных вычислениях

При решении физических задач числовые значения, с которыми приходится иметь дело, большей частью являются приближенными. Задачи с приближенными данными нужно решать с соблюдением правил подсчета значащих цифр. Значащими называются все цифры, кроме нуля, а также и нуль в двух случаях: 1) когда он стоит между значащими цифрами; 2) когда он стоит в конце числа и когда известно, что единицы соответствующего разряда в данном числе нет.

Приближенные вычисления следует вести с соблюдением следующих правил:

1. Так как с помощью вычислений получить результат более точный, чем исходные данные, невозможно, то достаточно производить вычисления с числами, содержащими не больше знаков, чем в исходных данных.

2. При сложении или вычитании приближенных чисел, имеющих различную точность, более точное число должно быть округлено до точности менее точного. Например:

9,6 + 0,176 = 9,6 + 0,2 = 9,8;

100,8 - 0,425 = 100,8 - 0,4 = 100,4.

3. При умножении и делении следует в полученном результате сохранять столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр. Например:

0,637 × 0,23 × 5,2 = 0,76, но не 0,761852;

6,32:3 = 2, но не 2,107.

4. При возведении в квадрат или в куб нужно сохранять столько значащих цифр, сколько их имеется в основании степени. Например:

1,23² = 1,51, но не 1,5129;

3,01³ = 27,3, но не 27,270901.

5. При извлечении квадратного или кубического корня в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число. Например:

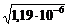= 1,09 × 10^-3, но не 1,09087 × 10^-3;

= 2,1, но не 2,154.

6. При вычислении сложных выражений соблюдаются указанные правила в зависимости от вида производимых действий. В промежуточных результатах следует сохранять на одну значащую цифру больше. Например: .

Сомножитель 3,1 имеет наименьшее число значащих цифр – две. Поэтому результаты всех промежуточных вычислений должны округляться до трех значащих цифр:

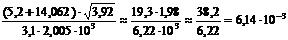
После округления результата до двух значащих цифр получаем 6,1×10^-3.

7. Если число незначительно отличается от единицы, можно пользоваться приближенными формулами.

Если а, b, с много меньше единицы (меньше 0,05), то можно принимать:

1)

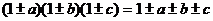
2)

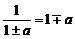
3)

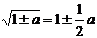
4)

5)

6)

7)

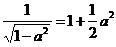
8)

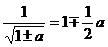
9)

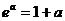
10)

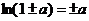
11)

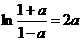
8. Если угол a<<5° и выражен в радианах, то в первом приближении можно принять: ; .

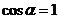Соблюдая эти правила, студент сэкономит время на вычислении искомых величин при решении физических задач.

УЧЕБНЫЕ МАТЕРИАЛЫ

Не нашли, что искали? Воспользуйтесь поиском: