Примеры для решения задач. Пример 8. На каком расстояннии друг от друга необходимо подвесить в теплицах, чтобы освещенность Е на поверхности земли в точке

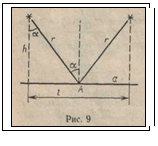Пример 8. На каком расстояннии друг от друга необходимо подвесить в теплицах, чтобы освещенность Е на поверхности земли в точке, лежащей посередине между двумя лампами, была не менее 200 лк? Высота теплицы h =2 м. Сила света каждой лампы I= 800 кд (рис.9).

Решение. Расстояние l между лампами можно определить из формулы прямоугольного треугольник (1)

Лампу можно принять за точечный источник света, так как ее размеры малы по сравнению с расстоянием до точки, в которой определяется освещенность. Поэтому найти расстояние r от лампы до точки А можно из формулы освещенности:

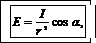(2)

где – угол, под которым падают лучи.

Подставив в (2) cos = h/ r, выразим r:

(3)

Подставим выражение (3) в (1):

(4)

Подставим числовые значения величин в (4)и вычислим

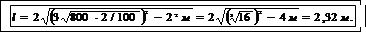
Пример 9. Фокусное расстояние объектива микроскопа f ₁=5 мм, окуляра f₂ =25 мм. Предмет находится на расстоянии

s =5,1 мм от объектива (рис.10).Вычислить длину тубуса микроскопа и даваемое микроскопом увеличение β.

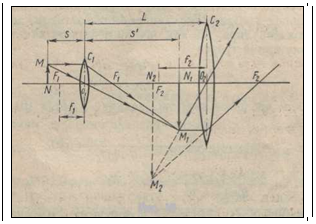Решение. Увеличение микроскопа

=β₁β₂, (1)

где β₁ – увеличение объектива; β₂ – увеличение окуляра, определяемые по формулам

β₁= /f₁; (2)

β₂=0,25/ f₂, (3)

где – Расстояние от объектива до даваемого им действительного изображения; 0,25 м – расстояние наилучшего видения для нормального глаза.

С учетом (2) и (3) формула (1) примет вид

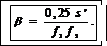(4)

Расстояние от объектива до изображения можно найти из формулы линзы:

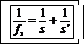
(s –расстояние от предмета до линзы), откуда

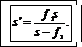
Подставив выражение для s ^׳ в (4), получим

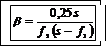. (5)

Выпишем величины, входящие в формулу (5), в СИ: s =5,1·10^-3 м, f ₁=5·10^-3 м, f₂ =25·10^-3 м.

Длину тубуса определим, исходя из следующих соображений. Действительное изображение, даваемое объективом, должно лежать в фокусе окуляра, так как окуляр действует как лупа (рис.10). Поэтому длина тубуса

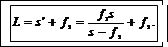(6)

Подставим числовые значения величин в (5)и (6) и вычислим

Пример 10. Определить число штрихов на 1 мм дифракционной решетки, если при нормальном падении света длиной волны λ =600 нм решетка дает первый максимум на расстоянии l =3,3 см от центрального. Расстояние от решетки до экрана L =110 см.

Решение. Число штрихов N на 1 мм решетки определим по формуле

N=1/d (1)

где d – период решетки (рис.11).

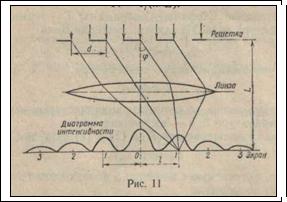
Период решетки найдем из условия максимума:

d sin φ= kλ, (2)

где φ – угол, под которым наблюдается r-й максимум; k – порядок (номер) максимума.

Ввиду того, что для максимума 1-го порядка угол мал, можно принять

sin φ=tgφ= l / L, (3)

Подставив в формулу (2) выражение синуса угла из (3), определим постоянную решетки:

D=kλL /l. (4)

C учетом (4) формула (1) примет вид

N=l / (kλL). (5)

Выпишем числовые значения величин, входящих в (5), в СИ: l= 3,3·10^-2 м, L =1,10 м, R= 1, λ=6·10^-7 м.

Подставим числовые значения величин в (5) и вычислим

Пример 11. Определиконцентрацию С сахарного раствора, если при прохождении света через трубку длиной l =20 см с этим раствором плоскость поляризации света поворачивается на угол φ=10⁰. Удельное вращение раствора сахара =0,6 град/(дм·%).

Решение. Из формулы для угла поворота плоскости поляризации определим концентрацию раствора:

Φ= Cl, (1)

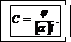(2)

Выпишем числовые значения величин, входящих в (2), в СИ: φ=10⁰, =6 град/(м·%), l =0,2 м.

Подставим числовые значения величин в (2) и вычислим

Пример 12. Максимум энергии излучения черного тела при некоторой температуре приходится на длину волны λ_m=1 мкм. Вычислить излучательность тела при этой температуре и энергию W, излучаемую с площади S =300 см² поверхности тела за время t =1 мин. Определить также массу, соответствующую этой энергии.

Решение. Излучательность черного тела определим из закона Стефана – Больцмана:

R₀= T ⁴, (1)

где – постоянная Стефана – Больцмана; Т – термодинамическая температура тела. Из закона смещения Вина

λ_m= b/Т

определим термодинамическую температуру:

Т=b/λ _m, (2)

где λ_m – длина волны, на которую прходится максимум излучения при температуре Т; b – постоянная Вина..

Подставив выражение для Т из (2) в (1), получим

R ₀= (b / λ _m)⁴, (3)

Энергию, излучаемую с площади S поверхности тела за время t, определим по формуле

W=R₀St. (4)

По закону Эйнштейна взаимосвязи энергии и массы

W=mc²

(с – скорость света в ваккуме; W – энергия) найдем массу соответствующую энергии излучения:

m=W/c², (5)

Проверим формулу (3):

Вт/м²=Вт/(м²·К⁴) (м·К/м)⁴=Вт/м².

Выпишем значения величин, входящих в формулы (3), (4), (5), в СИ: =5,67·10^-8 Вт/(м²·К⁴); = 2,89·10^-3 м·К, λ_m=10^-6 м, S= 3·10^-2 м²,t=60 c, c =3·10⁸ м/с.

Подставим числовые значения величин в формулы (3), (4), (5) и вычисли·м:

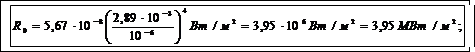
W= 3,95·10⁶·3·10^-2·60 Дж=7,10·10⁶ Дж=7,10 Мдж;

Пример 13. Для предпосевного облучения семян применен лазер, излучающий электромагнитные волны длиной λ=632 нм. Интенсивность излучения ĵ= 2·10³ Вт/м². Определить число фотонов, поглощенных семенем площадью S= 5 мм². Время облучения 10 мин.

Решение. Количество фотонов, поглощенных семенем, равно

п = W/ε, (1)

где ε – энергия фотона; W – энергия света, падающего на семя:

W=JSt. (2)

Здесь J – интенсивность излучения, т. е. энергия света, падающего на 1 м² за 1 с; S - площадь; t – время.

Энергию фотона определим по формуле Планка:

ε= hc/λ, (3)

где h – постоянная Планка; с – скорость света; λ – длина волны.

Подставив (2) и (3) в (1), получим

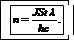(4)

Выпишем числовые значения величин, входящих в, (4), в СИ: S= 5·10^-4 м², t =600c, λ=632·10^-9 м, с= 3·10⁸ м/с, h= 6,63Х10^-34Дж·с.

Подставим числовые значения величин в (4) и вычислим

Пример 14. На поверхность площадью S =3 см² за время t =10 мин падает свет, энергия которого W =20 Дж. Определить: 1) облученность (энергетическую освещенность) поверхности, 2) световое давление на поверхности, если она или полностью поглощает лучи, или полностью отражает.

Решение. 1. Облученность определим по формуле

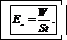
Выпишем значения величин, входящих в эту формулу, в СИ: S =3·10^-4 м², t =600 с.

Подставим числовые значения величин в расчетную формулу и вычислим

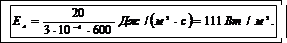
2.Световое давление определим по формуле

р = Е_е ( 1+ р) / с, или р = w (1+р),

где w = E_e / c – объемная плотность энергии излучения; с – скорость света в ваккуме; р – коэффициент отражения.

Если поверхность полностью поглощает лучи, то р =0 и тогда

Если поверхность полностью отражает лучи, то р =1 и тогда

р= 2·0,370 мкПа=0,740 мкПа.

Пример 15. Определить: 1) кинетическую энергию Т и 2) скорость фотоэлектронов при облучении натрия светом длиной волны λ=400 нм.

Решение. 1. Кинетическую энергию фотоэлектрона определим из формулы Эйнштейна для фотоэффекта:

hν = A + mύ² / 2, (1)

где h – постоянная Планка; – частота света; А – работа выхода электрона; Т = mύ² / 2 – кинетическая энергия фотоэлектронов; m – масса электрона; ύ – скорость электрона; Из формулы (1) следует

T = mύ² / 2 = hν - A.. (2)

Частоту света определим по формуле

(3)

где с – скорость света; λ – длина волны падающего света.

Для поверхности металла, освещенной светом частотой , соответствующей красной границе фотоэффекта, кинетическая энергия фотоэлектронов равна нулю и формула (1) примет вид

h = А..

Отсюда найдем работу выхода А=h , или

A=hc/λ _гр. (4)

Подставим в (2)формулы (3) и (4):

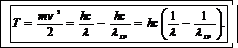(5)

Проверим формулу (5):

Выпишем числовые значения величин, входящих в формулу (5), в СИ: h =6,63·10^-34 Дж·с; с= 3·10⁸м/с, λ=4·10^-7 м, λ_гр=6·10^-7 м.

Подставим числовые значения величин (5) и вычислим

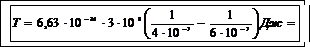
(1 эВ = 1,30^.10^-19 Дж).

2.Из формулы T=mύ² /2 определим скорость ύ фотоэлектронов:

Учитывая, что m =9,11·10^-31 кг, вычислим искомую скорость фотоэлектронов:

Пример 16. Определить энергию фотона, излучаемого атомомводородапри переходе электрона с третьего энергетического уровня на первый, а также длину электромагнитной волны, соответствующуюю этому фотону.

Решение. Переход электрона в атоме водорода с отдаленной орбиты на внутреннюю связан с излучением фотона (кванта энергии):

ε= h =hc/λ, (1)

где ε – энергия фотона; h – постянная Планка; с – скорость света в ваккуме; ,λ – частота и длина волны, соответствующие фотуну с энергией ε.

Длина волны излучаемого света связана с номером орбит соотношением

(2)

где R – постоянная Ридберга; п – номер энергетического уровня, на который переходит электрон; k – номер энергетического уровня, с которого уходит электрон.

Подставим в (2) R= 1,1·10⁷ м^-1, п =1, R= 3 и вычислим длину волны λ:

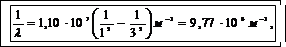
В выражение (1) подставим числовые значения величин с, λ и вычислим

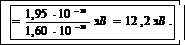
Пример 17. Навеска почвы, в которую внесено удобрение с радиоактивным фосфором ³²₁₅ Р,имеет активность а =10 мкКи. Определить массу m радиактивного фосфора в навеске. Период полураспада изотопа Т _1/2=14,28 дня.

Решение. Массу радиоактивного вещества можно определить из формулы

N=(m/M)N _A, (1)

где N – число атомов (ядер); m/M – число молей; m – масса вещества; М – масса млоя; N _A – постоянная Авогадро. Из формулы (1) определим

m=NM/N _A, (2)

Число атомов (ядер) N связано с активностью вещества соотношением

a=λN, (3)

где λ – постоянная распада, связанная с периодом полураспада зависимостью

λ=0,693/ (4)

Подставив (4) в (3), в затем в (2), получим

(5)

Выпишем значения величин, входящих в (5), в СИ: а =10·10⁴ Бк, М =32·10^-3 кг/моль, N _A=6,02·10²³ 1/моль, Т_1/2 =14,28·24·3600с.

Вычислим искомую массу радиоактивног препарата:

Пример 18. Определить дефект массы ∆ m и энергию связи ядра атома бора .

Решение. Дефект массы ядра представляет собой разность массы нуклонов (протонов и нейтронов), составляющих ядро, и массы ядра и определяется по формуле

∆ m= Zm _p + (A-Z)m_п - m _я, (1)

где Z – зарядное число (число протонов в ядре ); m _р - масса протона; А – массовое число (общее число нуклонов в ядре); (А-Z) – число нейтронов в ядре; m _я – масса ядра.

Числа Z и А указываются при,написании симола элемента: Z – слева вверху; в данном случае для бора Z =5, А= 10. Массу ядра найдем по формуле

(2)

где m_a – масса нейтрального атома; m_e – масса электрона.

Чтобы не вычяслять каждый раз массу ядра, преобразуем формулу (1) с учетом (2):

∆ m=Z +(A-Z)m_п-m_a. (3)

Из табл. 9 и 10 выпишем: m_1н1 =1,00783 а. е. м.^*, m _n=1,00867 а.е.м., m _a=10,01294 а. е.м.

Подставим числовые значения величин, входящих в (3), и вычислим дефект массыядра бора:

∆m=5·1,00783 а. е. м.+(10-5) ·1,00867 а.е.м.-10,011294 а.е.м.=0,06956 а.е.м.

Энергия связи ядра – энергия, выделяющеяся при образовании ядра в виде электромагнтитного излучения, - определяется по формуле

Е_св =∆ mc², (4)

где с – скорость света в ваккуме.

Если энергию связи Е _св выразить в мегаэлектрон – вольтах, деффект массы ∆ m ядра – в атомных единицах, то формула (4) примет вид

Е _св=931∆ m, (5)

где 931 – коэффициент, показывающий, какая энергия в мега-электрон-вольтах соответствует массе 1 а. е. м.. Подставим значение ∆ m в (5), вычислим энергию связи:

Е _св=931·0,06956 МэВ=64,8 МэВ.

Пример19. Вычислить энергию ядерной реакции

Выделяется или поглощается эта энергия?

Решение. Энергию ядерной реакции определим по формуле

∆ Е= 931 ∆ m, (1)

где ∆ m – изменение массы при реакции, т.е. разность между

*1 а.е.м.-это обозначение атомной единицы массы, в которой выражаются массы молекул атомов и элементарных частиц, 1 а.е.м.=^1/₁₂ массы атома изотопа углерода ¹²₆ С (1а.е.м.=1,66·10^-27 кг).

Массой частиц, вступающих в реакцию, и массой частиц, образовавшихся в результате реакции:

(2)

здесь – масса атома кислорода; – масса атома дейтерия (изотопа водорода); - масса атома изотопа; - маса изотопа гелия. По табл. 10 находим массы этих атомов и по формуле (2) вычисляем ∆ m:

∆ m =(15,99491+2,01410) а. е. м.-2 (14,00307+4,00260) а. е. м.=0,00334 а. е. м.

Подставим числовые значение ∆ Е =931·0,00334 МэВ=3,11 МэВ.

В результате ядерной реакции выделяется энергия, так как масса исходных ядер больше массы ядер, образовавшихся в результате реакции.

Не нашли, что искали? Воспользуйтесь поиском: