Примеры для решения задач

Пример 18. На непроводящей нити в воздухе подвешен шарик массой m=100 мг, несущий положительный заряд Q. Если снизу на расстоянии r=4 см поместить такой же шарик, натяжение нити исчезнет. Определить заряд шарика.

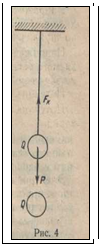Решение. При поднесении снизу шарика такой же массы и с таким же зарядом, как у подвешенного (рис 4), сила кулоновского отталкивания шариков уравновешивает силу тяжести шарика. При этом шарик находится в равновесии; следовательно,

F_K=Р (1)

Выразим в соответствии с законом Кулона силу F _к

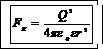, (2)

где – электрическая постоянная; – диэлектрическая проницаемость воздуха.

Подставив (2) и (1)и выразив силу тяжести Р через массу шарика m и ускорение свободного падения g, получим , откуда

(3)

Проверим формулу (3):

Выпишем числовые значения величин в СИ: m =10^-4 кг, r=4∙10^-2 м, g =9,81 м/с², =8,85∙10^-12 Ф/м, =1. Вычислим искомый заряд:

Пример 19. Два положительных заряда Q ₁=7 нКл и Q ₂=4 нКл находятся на расстоянии r=15 см друг от друга. Определить положение точки, в которую нужно поместить заряд Q₃, чтобы он находился в равновесии. Каков должен быть знак заряда Q ₃, чтобы равновесие было устойчивым?

Решение. Рассмотрим вопрос об устойчивости равновесия заряда Q ₃. Если заряд Q ₃ будет находиться на линии, соединяющей заряды Q₁ и Q₂, то каков бы ни был знак заряда Q ₃, силы его взаимодействия с зарядами Q ₁ и Q ₂ Следовательно, отыщется точка на которой силы, действующие противоположно на заряд Q ₃, будут уравновешены прямой АВ ( рис.5), в которой силы, действующие противоположно на заряд Q _3, будут уравновешенны.

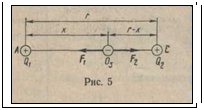Такая точка находится на расстоянии х от заряда Q ₃ до заряда Q ₁. При отклонении заряда Q ₃ от этой точки вправо или влево возникающее неравенство сил со стороны зарядов Q ₁ и Q ₂ будет неизменно возвращать заряд Q ₃ в положение равновесия. Рассмотрим теперь случай отклонения заряда Q ₃ перпендикулярно линии АБ. В том случае, если заряд положительный, при отклонении его вверх или вниз от положения равновесия силы отталкивания его зарядами Q ₁ и Q ₂ создадут равнодействующую, отбрасывающую заряд от линии АБ, на которой находится точка равновесия. Следовательно, при Q ₃>0положение равновесия не будет устойчивым. Если заряд Q ₃ отрицательный, то при его отклонении вверх и вниз от положения равновесия силы притяжения его зарядами Q ₁ и Q ₃ создают равнодействующие, возвращающие заряд Q ₃ на линию АВ. В этом случае равновесие заряда устойчиво.

Так как заряд Q ₃ находится в равновесии, то F ₁и F ₂ – cилы притяжения его соответственно зарядами Q ₁ и Q ₂ – равны между собой:

F₁=F₂.

Выразив F₁ и F₂ по закону Кулона, получим 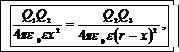или Извлекая из обеих частей равенства квадратный корень, находим 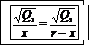, откуда

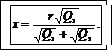
Выпишем числовые значения величин в СИ: r=0,15 м, Q₁ =7·10^-9 Кл, Q₂ =4·10^-9 Кл.

Вычислим искомое расстояние:

Пример 20. Два заряда Q ₁=9 нКЛ и Q ₂=-7 иКл расположены в вершинах равностороннего треугольника со стороной а =20 см. Определить напряженность и потенциал электрического поля в третьей вершине треугольника.

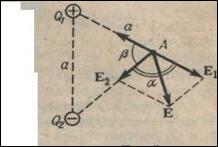Решение. 1. Напряженность электрического поля в точке А (рис.6) является геометрической (т.е. векторной) суммой напряженностей Е₁ и Е₂ полей, создаваемых зарядами Q ₁ и Q ₂ соответственно:

Е=Е₁+Е₂

Модуль результирующей напряженности может быть найден по теореме косинусов как диагональ параллелограмма, построенного на векторах Е₁ и Е₂:

(1)

Напряженность электрического поля точечного заряда выражается формулой

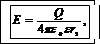(2)

где Q – заряд, создающий поле; – электрическая постоянная; – диэлектрическая проницаемость среды; r – расстояние от расчетной точки поля до заряда, его создающего.

Так как r=r₁=r₂= a, то имеем

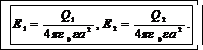(3)

Поскольку а =120⁰, преобразуем:

А=180 -β, cos(180)-β)=-cosβ. (4)

Подставим (3) и (4) в (1), получим

(5)

Выразим числовые значения величин в СИ: Q ₁=9·10^-9 КЛ, Q =-7·10^-9 Кл, =8,85·10^-12 Ф/м, =1, а =0,2 м, β=60⁰.

Проверим формулу (5):

Подставим в формулу(5) числовые данные и вычислим

Примечание. В расчетную формулу (5) подставлены модули зарядов, поскольку их знаки учтены при выводе этой формулы.

2.Потенциал электрического поля в точке А равен алгебраической сумме потенциалов φ₁ и φ₂ полей, создаваемых зарядами sQ₁ и Q₂ соответственно:

φ = φ₁+φ₂. (6)

Потенциал поля точечного заряда выражается формулой

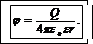(7)

В формуле (7) обозначения те же, что и в формуле (2). Подставив (7)в (6) и учитывая, что r=r₁=r₂= a

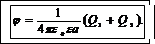(8)

Подставим числовые значения величин в (8) и вычислим:

Пример 21. Электрон, начальная скорость которого ύ₀=5 Мм/с, влетел в однородное электрическое поле перпендикулярно его линиям напряженности и пролетел его за время t =1 нс. Определить работу сил поля, скорость покидающего поле электрона и отношение работы сил поля к приращению кинетической энергии электрона. Напряженность поля Е =10 кВ/м.

Решение. На электрон, находящийся в электрическом поле, действует сила

F=eE, (1)

где е –заряд электрона.

Направление этой силы противоположно направлению вектора напряженности поля, т. е. перпендикулярно вектору скорости электрона. Работа этой силы выражается формулой

A=eU, (2)

где U = φ₀-φ – потенциалов между начальной и конечной точками траектории электрона в поле.

В однородном электрическом поле, где эквипотенциальные поверхности являются плоскостями, перпендикулярными линиями напряженности поля, разность потенциала выражается формулой

U=Tl, (3)

где l – расстояние между эквипотенциальными поверхностями φ₀ и φ (рис.7).

РИС.7

Движение электрона в электрическом поле по условию задачи является сложным движением, состоящим из двух взаимно перпендикулярных простых движений: равномерного со скоростью ύ₀ и равноускоренного в направлении действия силы F. Последнее началось в момент влета электрона в электрическое поле. Скорость равноускоренного движения из состояния покоя (движение, параллельное линиям напряженности электрического поля) выражается формулой

ύ_‼ = at, (4)

где а – ускорение, определяемое, в свою очередь, по второму закону Ньютона:

a=F/m_e, (5)

где m_e – масса электрона.

Величина l – расстояние, пройденное электроном при равноускоренном движении из состояния покоя за время t нахождения электрона в поле, может быть выражено так:

l=at²/2

Подставив последовательно (1) в (5) и в выражение для l, а затем в (3) и, наконец, в (2), получим

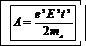. (6)

Проверим формулу (6):

Выпишем числовые значения величин в СИ: е= 1,6·10^-18 Кл, Е= 10⁴ В/м, t =10^-9 с, m_e =9,11·10^-31 кг (см. табл.1).

Подставим числовые значения величин в (6) и вычислим

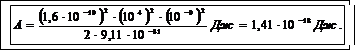
В соответствии с правилами векторного сложения скоростей в конечной точке пути электрона в поле имеем

v=v ₀ +v _‼,

или, учитывая, что v₀ v_‼ ,

(7)

Подставив (1) в (5), затем в (4) и, наконец, в (7), получим

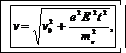(8)

где ύ₀=2·10⁶ м/с

Подставим числовые значения величин в (8) и вычислим

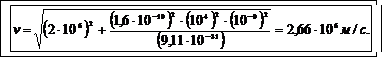
Отношение работы поля к приращению кинетической энергии электрона выразим формулой

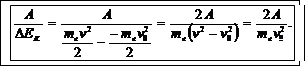(9)

Из формулы имеем (8) имеем

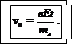(10)

Подставим (6) и (10) в (9), получим

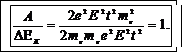
Пример 22. Плоский конденсатор, расстояние между пластинами которого d₁=10 см, заряжен до разности потенциалов U ₁=250 В и отключен от источника. Площадь пластин конденсатора S=100 см². Определить заряд конденсатора. Как изменятся емкость, разность потенциалов, энергия его поля, если в пространство между ними поместить фарфоровую плитку толщиной d₂=2 см и прижать к ней пластины?

Решение. Емкость конденсатора называют величину, равную отношению заряда конденсатора к разности потенциалов между пластинами:

C=Q/U_1. (1)

Зависимость емкости конденсатора от его размеров выражается формулой

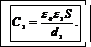(2)

Выразив из (1) искомый заряд и подставив (2) в полученную формулу, находим

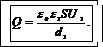(3)

Проверим правильность формулы (3):

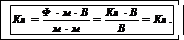
Выпишем числовые значения величин в СИ: =8,85X10^-12 Ф/м, =1, S=10^-2 м², d ₁=0,1 м, U =250 В.

Подставим числовые значения величин в (3) и вычислим

Из формулы (2) видно, что изменение вида диэлектрика и расстояния между пластинами конденсатора приводит к изменению его емкости:

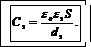(4)

Разделив почленно (2) на (4), получим

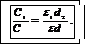(5)

Вычислим это отношение, учитывая, что =5 (см. табл. 8), d ₂=2·10^-2 м:

Следовательно, емкость конденсатора увеличилась в 25 раз.

Из формулы (1) получим разности потенциалов для начального и конечного состояний конденсатора:

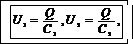откуда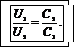

Используя (5), получаем

(6)

Подставив числовые значения в (6), получим

Следовательно, напряжение на конденсаторе уменьшается в 25 раз.

Энергия поля конденсатора в его начальном и конечном состоянии выражается формулами

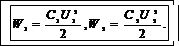
Отсюда выражаем отношение энергией:

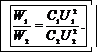(7)

Подставив (5) и (6) в (7), получим

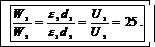
Следовательно, энергия конденсатора уменьшается в 25 раз.

Объемная плотность энергии поля – это энергия, заключенная в единице объема:

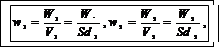
где V₁=Sd₁ и V₂=Sd₂ – объемы пространства между пластинами конденсатора в его начальном и конечном состояниях соответственно. Отсюда отношение.

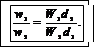(8)

Подставив числовые значения величин в (8), получим

Следовательно, объемная плотность энергии уменьшилась в 5 раз.

Пример 23. Электродвигатель работает в сети с напряжением U =120 В. Мощность двигателя N =1,2 кВт, коэффициент полезного действия =75%. Определить силу тока, потребляемую двигателем, и сопротивление его обмоток.

Решение. Мощность двигателя

N=IU,

где I – сила тока, потребляемая двигателем. Отсюда

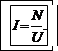
Выпишем числовые значения величин в СИ: N =1,2·10³ Вт, U =120 В.

Подставим значения величин в расчетную формулу и вычислим

Коэффициент полезного действия двигателя

(1)

где N ₁ – полезная мощность:

N₁=N-N₂, (2)

N₂ – мощность, расходуемая на нагревание обмоток двигателя;

N₂ =I² r, (3)

здесь r – сопротивление обмоток.

Подставив (3) в (2) и затем в (1), получим 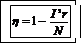, откуда

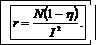(4)

Подставим числовые значения величин в (4)и вычислим

Пример 24. Три одинаковых источника тока с ЭДС Е=1,5 В каждый соединены параллельно и создают в цепи ток I =1 А. Определить коэффициент полезного действия батареи, если внутреннее сопротивление каждого источника тока r=0,3 Ом.

Решение. При параллельном подключении одинаковых источников тока их общая электродвижущая сила равна ЭДС одного источника. В то же время батарея источников создает разветвленный участок цепи, общее сопротивление которого может быть найдено из формулы проводимости группы параллельно соединенных элементов:

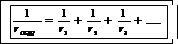(1)

Поскольку в нашем случае группа параллельно соединенных элементов образована батарей из трех источников тока с общим сопротивлением r_б а r₁=r₂=r₃=r, формулу (1) можем записать в виде

R_б=r/3. (2)

Батарея источников тока замыкается потребителем электроэнергии, сопротивление которого R _п. Тогда на основании закона Ома для замкнутой цепи

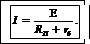
Отсюда

Е=IR_п+I r _б=U+I r_б, (3)

где U – разность потенциалов на зажимах батареи источников электроэнергии. Коэффициент полезного действия батареи

= U/Е (4)

Из (3) следует, что

U=Е-Ir_б, (5)

Подставив (2)в (5) и затем в (4), получим

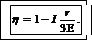(6)

Подставим числовые значения величин в (6) и вычислим

Пример 25. Термопара с сопротивлением r=6 Ом включена в цепь с гальванометром, сопротивление которого r₂=4 Ом. Чувствительность гальванометра I₀ =5·10^-2мкА. Какое минимальное изменение температуры позволяет определить это измерительное устройство, если постоянная термопары k =5·10^-2 мВ/⁰С?

Решение. Минимальное изменение температуры, фиксируемое данным измерительным устройством, соответствует смещению стрелки гальванометра на одно деление. Цена одного деления гальванометра называется его чувствительностью. Следовательно, искомая величина равна разности температур спаев термопары, при которой гальванометр покажет одно деление, т.е. ток I₀

Электродвижущая сила термопары, согласно принципу ее действия, пропорциональна разности температур спаев ∆ t:

(1)

Согласно закону Ома для замкнутой цепи,

Е= i (r₁ +r₂ ), (2)

Приравняв правые части формул (1) и (2), получим k∆t = I(r₁ +r₂ ) откуда, учитывая сказанное выше,

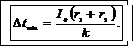(3)

Выпишем числовые значения величин в СИ: I₀ =5^.10^-8 A, r₁ =6Ом, r₂ =4Ом, k=5^.10^-5 В/ºС.

Подставим числовые значения величин в (3) и вычислим

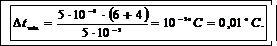
Не нашли, что искали? Воспользуйтесь поиском: