Примеры для решения задач. Пример.По двум длинным прямолинейными параллельным проводам, расстояние между которыми d=8 см, в противоположных направлениях текут токи I1=3 А

Пример. По двум длинным прямолинейными параллельным проводам, расстояние между которыми d= 8 см, в противоположных направлениях текут токи I ₁=3 А, I ₂=5 А. Найти магнитную индукцию поля в точке А, которая находится на расстоянии r₁=2 см от провода на линии, соединяющей провода (рис. 8)

Решение. На рис. 8 провода расположены перпендикулярно плоскости чертежа. Маленькими кружочками изображены сечения проводов. Условимся, что ток I ₁ течет к нам, а ток I ₂ -от нас. Общая индукция В в точке А равна векторной (геометрической) сумме индукций В ₁ и В ₂ полей, создаваемых каждым током в отдельности:

В=В ₁+ В ₂ (1)

Для того чтобы найти направление векторов В ₁ и В ₂, проведем через точку А силовые линии магнитных полей, созданных токами I ₁ и I ₂. Силовые линии магнитного поля прямого провода с током представляют собой концентрические окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого по направлению тока (правило буравчика). Поэтому силовая линия магнитного поля тока I ₁, проходящая через точку А, представляет собой окружность радиусом I ₁ А, силовая линия магнитного поля тока I ₂ проходящая через эту же точку - окружность радиусом I ₂ A (на рис. 8 показана только часть этой окружности).

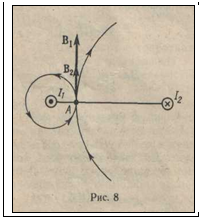По правилу буравчика находим, что силовая линия магнитного поля тока I ₁ направлена против часовой стрелки, а тока I ₂-по часовой стрелке.

Теперь легко найти направления векторов В ₁ и В ₂ в точке А: каждый из них направлен по касательной к соответствующей силовой линии в этой точке. Так как векторы В ₁и В ₂ направлены вдоль одной прямой в одну сторону, то векторное равенством (1) можно заменить скалярным равенством

В=В₁+В_2. (2)

Индукция магнитного поля тока I, текущего по прямому бесконечно длинному проводу, вычисляется по формуле

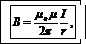(3)

где μ₀-магнитная постоянная; μ -магнитная проницаемость среды, в которой провод расположен; r-расстояние от провода до точки, в которой определяется индукция.

Подставив выражение (3) для В ₁ и В ₂ в равенство (2), получим

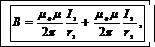
или

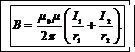(4)

Выпишем в СИ числовые значения величин: r₁=0,02 м, r₂=d - r=0,06 м, μ₀=4π·10^-7 Гн/м, μ=1.

Вычислим искомую индукцию:

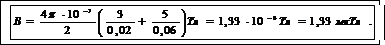
Пример 2. На виток проволоки, имеющей сопротивление R =0,5 Ом, подается напряжение U= 10 В. Определить: 1)индукцию магнитного поля в центре витка; 2) магнитный момент витка, если его диаметр 20 см; 3) максимальный вращающий момент, если виток поместить в магнитное поле с индукцией В =5 Тл.

Индукция магнитного поля в центре витка с током определяется по формуле

, (1)

где I – сила тока; μ₀ – магнитная постоянная; r – радиус витка; μ – относительная магнитная проницаемость среды.

Из закона Ома находим силу тока:

I=U/R.. (2)

Подставляя формулу (2) в (1), получим

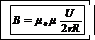. (3)

Выпишем числовые значения величин, входящие в формулу (3), в СИ: U =10 В, μ₀=4π·10^-7 Гн/м, μ=1, r=10 см=0,1 м, R =0,5 Ом.

Вычислим искомую индукцию:

2.Магнитный момент р_m замкнутого плоского контура с током I определим по формуле

=IS, (4)

где S – площадь контура.

Выражение площади S=π r² подставим в формулу (4):

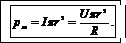
Вычислим магнитный момент:

Вращающий механический момент, действующий на виток с током, определим по формуле

М= В sin a, (6)

где – магнитный момент; В – магнитная индукция; – угол между направлениями тока и индукции поля.

При =90⁰ механический момент максимален.

Подставим числовые значения величин в (5) и вычислим

М= 0,63·5Нм=3,15Нм.

Пример 3. Катушка длиной l =10 см и площадью сечения S =30 см² имеет 12 витков на 1 см длины. Индукция поля в катушке равна В =8·10^-3Тл. Определить: 1) силу тока в катушке; 2)энергию магнитного поля.

Решение.1. Индукцию магнитног поля на оси соленоида определим по формуле

В=μ₀ μ пI, (1)

где п – число витков на единицу длины катушки; I – сила тока, протекающего по виткам.

Из формулы (1) определим силу тока:

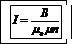. (2)

Выпишем величины, входящие в формулу (2), в СИ: μ₀=4π·10^-7 Гн/м, μ=1, п =12 см^-1=1200 м^-1, В= 8·10^-3 Тл.

Подставим числовые значения величин в (2) и вычислим

2.Определим энергию магнитного поля по формуле

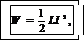(3)

где L – индуктивность катушки; I – сила тока.

Индуктивность катушки находим по формуле

L= μ₀μ п²V, (4)

где μ – магнитная проницаемость среды; μ₀ – магнитная постоянная; п – число витков на единицу длины; V –объем катушки.

Объем катушки равен

V=Sl, (5)

где S и l – соответственно площадь сечения и длина катушки.

Подставим в формулу (3) выражения (4) и (5):

(6)

Выпишем значения величин, входящих в формулу (6), в СИ: μ=1, μ₀=4π·10^-7 Гн/м, п =1200, S =30 см²=30·10^-4 м², l =10 см=0,1 м, I =5,3 A.

Подставим значения величин в (6)и вычислим

Пример 4. Заряженная частица движется в магнитном поле по окружности со скоростью ύ=10⁶ м/с. Индукция магнитного поля В=0,3 Тл. Радиус окружности r=4 см. Определить: 1)заряд частицы, если известно, что ее энергия равна Т =1,2·10⁴ эВ, 2)ускоряющую разность потенциалов, придавшую скорость частице.

Решение. 1. На заряженную частицу, движущаяся в магнитном поле, действует сила Лоренца, определяемая по формуле

F_л =Q Вύ sin , (1)

где Q – заряд частицы; В – магнитная индукция поля; ύ – скорость частицы; – угол между векторами скорости и магнитной индукцией.

Сила Лоренца обусловливает центростремительное направление этой силы:

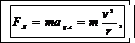(2)

где m – масса частицы; ύ – ее скорость; r – радиус окружности.

Приравнивая правые части уравнений (1) и (2), получим

QВύ sin a = mύ² /r. (3)

Уравнение (3) решим относительно Q:

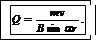(4)

Движущаяся частица обладает кинетической энергией, которую определим по формуле

Т=mύ²/2 (5)

Из уравнения (5) определим массу частицы и ее выражение подставим в формулу (4):

(6)

Выпишем величины, входящие в (6), в СИ: Т= 1,2·10⁴ эВ=12·1,6·10^-16 Дж, ύ=10⁶ м/с, В=0,3 Тл, r=4 см=0,04 м, =90⁰ (так как вектор скорости перпендикулярен вектору индукции поля, частица движется по окружности).

Подставим значения величин в (6) и вычислим

2.По закону сохранения энергии, работа, совершенная электрическим полем при перемещении заряженной частицы, равна кинетической энергии, приобретенной частицей, т. е.

A=mύ²/2=Т (7)

Работа поля по перемещению заряда определяется по формуле

А=QU, (8)

где Q – заряд частицы; U – ускоряющая разность потенциалов.

Подставив (8) в (7), выразим искомую разность потенциалов:

U=Т/Q. (9)

Подставив в (9) числовые значения величин в СИ, получим

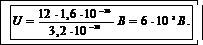
Пример 5. Проволока длиной l= 20 см и площадью сечения S =10 см², намотанная на картонный цилиндр и содержащая N =500 витков, присоединена параллельно к конденсатору емкостью С =889 пФ. На какую длину волны будет резонировать контур?

Решение. Длину волны можно определить по формуле

λ= сТ, (1)

где с – скорость распространения электромагнитных волн; Т – период колебания контура.

Период колебания контура связан с индуктивностью и емкостью контура соотношением

(2)

где L – индуктивность катушки; С – емкость конденсатора.

Индуктивность катушки определим по формуле

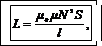(3)

где μ – магнитная проницаемость; μ₀ – магнитная постоянная.

Подставляя выражение индуктивности (3) в формулу (2), получим

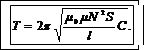(4)

В формулу (1) подставим выражение (4):

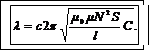(5)

Выпишем значения величин, входящих в формулу (5), в СИ: с =3·10⁸ м/с, μ=1, μ₀=4π·10^-7 Гн/м, N= 500, S= 10 см²=10^-3 м², l =20 см=0,2 м, С= 889·10^-12 Ф.

Подставим числовые значения величин в (5) и вычислим

Пример 6. Плоская рамка площадью S =100 см², содержащая N =20 витков тонкого провода, вращается в однородном магнитном поле с индукцией В= 100 мТл. Амплитуда ЭДС индукции & _maх=10 В. Определить частоту вращения рамки.

Решение. Используя понятие угловой скорости вращения (ω=2π/ Т =2π п, где Т – период вращения; п – частота вращения), определим частоту вращения рамки:

п=ω /(2π). (1)

Угловую скорость вращения найдем из соотношения

Е = NВSω sin ω t, (2)

где & – мгновенное значение ЭДС индукции.

Амплитудой Е является значение Е _maх, соответствующее значению sin ω t =1. Из соотношения (2) имеем

(3)

Подставив выражение (3) в (1), получим

(4)

Выпишем значения величин, входящих в формулу (4), в СИ: В =0,1Тл, S =10^-2 м^2.

Подставим числовые значения величин в (4)и вычислим

Пример 7. На немагнитный каркас длиной l =50 см и площадью сечения S =3 см² намотан в один слой провод диаметром d =0,4 мм так, что витки плотно прилегают друг к другу. Определить: 1) индуктивность получившегося соленоида; 2) магнитный поток, пронизывающий сечение соленоида при токе I =1 A.

Решение. 1. Индуктивность соленоида вычислим по формуле

L =μ₀μ п²V, (1)

где п – число витков, приходящихся на еденицу длины на диаметр провода:

п =1/ d, (2)

Объем соленоида равен

V=Sl, (3)

где S – площадь поперечного сечения соленоида; l – длина соленоида.

Подставим выражения (2) и (3) в равенство (1):

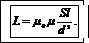(4)

Выпишем числовые значения величин, входящих в (4), в СИ: l =0,5 м, S =3·10^-4 м², d =4·10^-4 м, μ₀=4·10^-7 Гн/м, μ=1.

Подставим числовые значения величин в (4) и вычислим

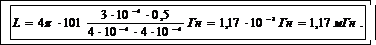
2.При наличии тока в соленоиде любое его поперечное сечение площадью S пронизывает магнитный поток

Ф_m= ВS, (5)

где В – магнитная индукция в соленоиде.

Магнитную индукцию соленоида определим по формуле

В=μ ₀μ Iп.. (6)

Подставим выражения (2) и (6) и (5), получим расчетную формулу

(7)

Подставим в формулу (7) числовые значения величин в СИ и вычислим

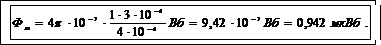
Не нашли, что искали? Воспользуйтесь поиском: