Примеры решения задач. Пример 8. Определить плотность смеси газов: v1=5 моль азота и v2=10 моль кислорода, - содержащихся в баллоне при температуре t=170С и давления р=2,5 Мпа.

Пример 8. Определить плотность смеси газов: v₁=5 моль азота и v₂=10 моль кислорода, - содержащихся в баллоне при температуре t=17⁰С и давления р =2,5 Мпа.

Решение. Согласно определению плотности имеем

P=(m₁+m₂)/V, (1)

где m₁ и m₂ – массы азота и кислорода соответственно; V – молярную массу:

m₁=v₁M₁, m₂₌v₂M₂. (2)

Для определения объема газа в баллоне воспользуемся уравнением Менделеева – Клапейрона для смеси газов:

=(m₁ /M₁+m₂ /M₂)RT=(v₁+v₂)RT,

где R – молярная газовая постоянная; Т – термодинамическая температура.

Тогда

V=(v₁+v₂)RT/p _см. (3)

Подставив выражения (2) и (3) в (1), получи

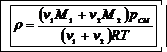. (4)

Проверим формулу (4):

Запишем величины, входящие в (4), в единицах СИ: М ₁=28·10^-3 кг/моль, М₂ =32·10^-3кг/моль, R =8,31 Дж/(моль·К), р _см=2,5·10⁶ Па, Т =290 К.

Вычислим искомую плотность:

Пример 9. Определить: 1)число атомов, содержащихся в 1 кг гелия; 2)массу атома гелия.

Решение.1. Число молекул в данной массе газа

N=vN_A=mN_A /M, (1)

где m – масса газа; М – молярная масса; =m/M - количество вещества, N _A – постоянная Авогадро.

Поскольку молекулы гелия одноатомны, число атомов в данной массе газа равно числу молекул.

Запишем величины, входящие в формулу (1), в СИ: М =4·10^-3 кг/моль, N _A=6,02·10²³ моль^-1.

Найдем искомое число атомов:

2.Для определения массы m₁ одного атома массу газа разделим на число атомов в нем:

m_i=m/N. (2)

Подставив числовые значения величин в (2), получим

Пример 10. Считая водяной пар массой m =180 г при температуре t =127⁰С идеальным газом, определить; 1) внутреннюю энергию пара; 2)среднюю энергию вращательного движения одной молекулы этого пара.

Решение.1. Внутренняя энергия идеального газа есть полная кинетическая энергия всех молекул газа; она выражается формулой

U=imRT/(2M), (1)

где i – число степеней свободы молекулы газа; М – молярная масса; R – молярная газовая постоянная; Т – термодинамическая температура.

Проверим формулу (1):

Запишем числовые данные в СИ: m =0,18 кг, Т = 400 К, М =18·10^-3 кг/моль, R =8,31 Дж/(моль·К), i =6, так как молекула водяного пара трехатомная.

Вычислим искомую внутреннюю энергию:

2.Известно, что на каждую степень свободы молекулы газа приходится в среднем энергия

< w ₀>= RT/2,

где R – постоянная Больцмана. Вращательному движению каждой молекулы приписывается некоторое число степеней свободы . Это относится ко всем молекулам, кроме одноатомных, для которых энергия вращательного движения равна нулю, как для материальных точек, размещенных на оси вращения. Таким образом, энергия вращательного движения молекулы

Выпишем числовые значения величин в единицах СИ: R =1.38·10^-23 Дж/К; =3, так как вращательному движению трехатомной молекулы соответствуют три степени свободы.

=3·1/2·1,38·10^-23·400Дж=8,28·10^-21 Дж.

Пример 11. Кислород массой m =320г изобарно расширяется под давлением р =2·10⁵ Па от начальной температуры t ₁=20⁰С, поглощая в процессе расширения теплоту Q =10 кДж. Определить: 1)работу расширения газа; 2)конечный объем газа.

Решение.1.Работа, совершаемая газом при неизменном давлении, выражается формулой

A=p(V₂-V ₁). (1)

Из уравнения Менделеева – Клапейрона, записанного для начального и конечного состояний газа (pV₁=mRT₁ /M, pV₂=mRT₂ /M), выразим неизвестные начальной V₁ и конечный V₂ объемы:

V₁=mRT₁ /(pM); (2)

V₂=mRT₂ /(pM). (3)

Подставив (2) и (3) в (1), получим

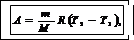(4)

где М – молярная масса кислорода; R – молярная газовая постоянная; T₁ и T₂ – начальная и конечная температуры газа.

Из формулы для теплоты при изобарном процессе

где с _р – удельная теплоемкость газа при постоянном давлении, выразим неизвестную разность температур:

Т₂-Т₁=Q/(mc _p). (5)

Известно, что

c _p=(i+2)R/(2M), (6)

где i – число степеней свободы молекулы газа. Подставив (6) в (5), а затем результат в (4), получим

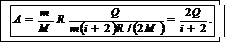(7)

Запишем в единицах СИ числовые значения величин: Q =10⁴ Дж, i=5, так как молекула кислорода двухатомная.

По формуле (7) вычислим А:

2.Для определения конечного объема V₂ воспользуемся формулой (1), преобразовав которую получим

V₂=(1/p) (A+pV₁). (8)

Второе слагаемое в скобках, содержащее неизвестную величину V₁, можем определить из уравнения Менделеева – Клапейрона для начального состояния газа.

Подставив в (8) правую часть уравнения (2), получим

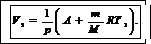
Выразим в единицах СИ числовые значения величин, входящих в эту формулу: М =32·10^-3 кг/моль, Т =293 К, m =0,32 кг, R =8,31 Дж/(моль·К).

Вычислим искомый конечный объем:

Пример 12. Определить: 1)среднюю длину свободного пробега < l > и 2)среднюю частоту столкновений < z > молекул воздуха при температуре t =0⁰С и давлении 1,01 Па. Принять эффективный диаметр молекулы воздуха равным d =2,9·10^-8 см.

Решение.1. средняя длина свободного пробега молекулы выражается формулой

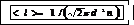(1)

где п – концентрация молекул (отношение числа молекул к объему газа, в котором они заключены). Для определения неизвестной концентрации молекул воспользуемся основным уравнением молекулярно – кинетической теории:

р =2/3n <w _пост>. (2)

Здесь р – давление газа, < w _пост> - средняя энергия поступательного движения молекулы газа, равная

< w _пост>=3/2 kT, (3)

где k – постоянная Больцмана, Т – термодинамическая температура газа.

Подставив (3) в (2), выразим из полученной формулы концентрацию молекул:

п=p/(kT). (4)

Подставив (4) в (1), получим

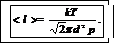
Проверим полученную формулу:

м=Дж·К·м²/(К·м²·Н)=Н·м/Н=м.

Выпишем величины, входящие в формулу, в единицах СИ: Ŗ=1,38·10^-23 Дж/К, Т =273 К, d =2,9·10^-10м.

Вычислим искомую длину свободного пробега молекулы:

2.Средняя частота столкновений молекул газа связана с длиной свободного пробега соотношением

(5)

где <ύ> - средняя арифметическая скорость молекул. Ее можно определить по формуле

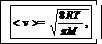(6)

где R- молярная газовая постоянная; М- молярная масса воздуха..

Подставив (6)в (5), после преобразования получим

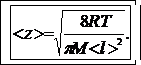(7)

Проверим формулу (7)

Выпишем в СИ недостающие для формулы (7) числовые данные: R =8,31 Дж/ (моль∙К), М=29∙10^-3 кг/моль.

Вычислим искомую частоту столкновений:

Пример 13. Определить среднюю квадратичную скорость молекул идеального газа при давлении р =1,01∙10⁴ Па, если плотность газа р =0,2кг/м³

Решение. Средняя квадратичная скорость молекул идеального газа выражается формулой

(1)

где R –молярная газовая постоянная; Т – термодинамическая температура газа; М – молярная масса.

Для определения неизвестных величин Т и М воспользуемся уравнением Менделеева – Клапейрона:

PV=(m/M)RT,

Откуда

(2)

Подставим RT/M (2)в (1), получим

(3)

Проверим формулу (3):

Вычислим искомую скорость молекул:

Пример 14. Определить, при каком градиенте плотности углекислого газа через каждый квадратный метр поверхности почвы продиффундирует в атмосферу в течение 1 ч масса газа m =720 мг, если коэффициент диффузии D =0,04 см³/с.

Решение. Масса газа, переносимая в результате диффузии, определяется законом Фика:

(1)

где D –коэффициент дифузии; ∆ р ∆ х – грдиент плотности, т. е. изменение плотности, приходящиеся на 1 м толщины слоя почвы; S – площадь поверхности слоя; t – длительность диффузии.

Из (1) выразим искомый градиент плотности:

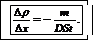(2)

Проверим формулу (2):

кг/м³∙м = кг/(м²/с) м²∙с= кг/м⁴.

Выпишем числовые значения всех величин, входящих в формулу (2), в единицах СИ: m =7,2∙10^-4кг, D =4∙10^-6 м²/с, S =1 м², t =3,60∙10³ с.

Вычислим градиент плотности:

Отрицательное значение градиента плотности соответствует сущности процесса диффузии: зависимость плотности от расстояния в направлении движения диффундирующий массы выражается убывающей функцией, градиент которой – отрицательная величина.

Пример 15. Определить количество теплоты, теряемое через бетонные стены родильного отделения фермы КРС площадью S =50 м² за время t =1 мин, если в помещении температура стены t₁ =15⁰C, а снаружи t ₂=-10⁰С. Толщина стен ∆ х =25 см.

Решение. Количество теплоты, передаваемое за счет теплопроводности стен, выражается законом Фурье:

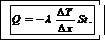(1)

где λ – теплопроводность материала стены; ∆ Т /∆х – градиент температуры, т. е. изменение температуры, приходящееся на 1 м толщины стены; S – площадь поверхности стены; t – время передачи теплоты.

Проверим формулу (1):

Дж= Дж/(м∙с∙К) ∙(К/м)∙м^2∙Дж.

Выразим числовые значения всех величин в СИ: ∆ Т=t₂-t₁=T₂-T₁=-10⁰ C-15⁰C=-25⁰C=-25 К, ∆ х =0,25 м, S =50 м², t= 60c, =0,817 Дж/(м·с·К) (см. табл 6).

Подставим числовые значения величин в формулу (1) и вычислим

Пример 16. Воздух, взятый при температуре t₁ =0⁰С, был адиабатно сжат так, что его объем уменьшился в тир раза. Определить температуру воздуха после сжатия.

Решение. Зависимость между температурой и объемом при адиабатном сжатии выражается уравнением Пуассона:

(1)

где T ₁,V₁ – соответственно термодинамическая температура и объем до сжатия воздуха; T₂, V₂ – те же величины после сжатия воздуха; – отношение теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.

Из теории теплоемкостей газов известно, что

= (i+2)/ i,

где i – число степеней свободы молекулы газа. Так как воздух-газ двухатомный, то i =5и, следовательно,

= (5+2)/5=1,4.

Из формулы (1) получим

T₂=T₁(V₁/V₂) (2)

Подставим числовые значения (Т₁= 273 К, =1,4, V₁/V₂ =3) в (2):

Т₂= 273·3^1,4-1К=273·3^0,4К.

Прологарифмируем обе части полученного равенства:

lg T₂ = lg273+0,41g3=2,463+0,4·0,477=2,6268.

По значению lg T₂, пользуясь таблицей антилогарифмов, найдем

Т₂ = 424К, или t ₂ = (Т ₂-273)⁰С = (424-273)⁰С = 151⁰С.

Пример 17. Нагреватель тепловой машины, работающей по циклу Карно, имеет температуру t ₁=197⁰C. Определить температуру охладителя, если ¾ теплоты, полученной от нагревателя, газ отдает охладителю.

Решение. Термический КПД тепловой машины, работающей по циклу Карно, выражается формулой

=(Т₁-Т₂)/Т₁, (1)

или, как и для любого цикла,

=(Q₁-Q₂)/Q₁, (2)

где Т₁ и Т ₂ – соответственно термодинамические те пературы нагревателя и охладителя; Q₁ – теплота, полученная газом от нагревателя; Q₂ – теплота, отданная газом охладителю.

Приравняв правые части формулы (1) и (2), получим

(Т₁-Т₂)/Т₁=(Q₁-Q₂)/Q₁. (3)

После простых преобразований уравнение (3) примет вид Т₂ /Т ₁= Q₂/Q₁, откуда

Т₂=Т ₁ Q₂ /Q ₁. (4)

Подставим числовые значения [ Т ₁ =(197+273) К=470 К, Q ₂= ³/₄Q₁] в (4) и вычислим:

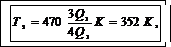или t₂ =79^º C

Не нашли, что искали? Воспользуйтесь поиском: