Примеры решения задач по теме. «Электромагнитные колебания и волны»

«Электромагнитные колебания и волны»

Задача 1. Разность потенциалов между обкладками конденсатора емкостью 0,5 мкФ в колебательном контуре изменяется со временем по закону U = 100 sin1000pt [ B ]. Определить период собственных колебаний, индуктивность, полную энергию контура и максимальную силу тока, текущего по катушке индуктивности. Активным сопротивлением контура пренебречь.

Дано:

;

U_m = 100 B;

ω = 10³ рад/с

T =? ω =? I_m =? L =?

Решение.

Напряжение на конденсаторе изменяется по гармоническому закону

, (1)

где U_m - амплитудное (максимальное) значение напряжения на обкладках конденсатора;

w _- собственная круговая частота колебаний, которая связана с периодом соотношением

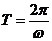. (2)

Отсюда находим:

.

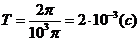Период собственных колебаний в контуре определяется по формуле Томсона:

. (3)

Следовательно,

. (4)

Проверка размерности расчетной формулы:

Вычисление:

.

Полная энергия контура складывается из энергии электрического поля W_э конденсатора и энергии магнитного поля W_м катушки:

. (5)

Полная энергия контура равна максимальной энергии электрического поля конденсатора:

(6)

или максимальной энергии магнитного поля катушки:

. (7)

Проверка размерности расчетных формул:

.

Вычисление:

.

Ответ: период собственных колебаний контура равен 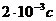; индуктивность катушки равна 0,2 Гн; полная энергия колебательного контура равна ; максимальная сила тока, текущего по катушке равна 0,16 А.

Задача 2. Длина электромагнитной волны в вакууме, на которую настроен колебательный контур, равна 12 м. Пренебрегая активным сопротивлением контура, определить максимальный заряд 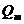на пластинах конденсатора, если максимальная сила тока в контуре

Дано:

Решение.

Согласно закону сохранения энергии

, (1)

где - максимальная энергия электрического поля конденсатора;

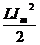- максимальная энергия магнитного поля катушки.

Длина электромагнитной волны в вакууме

, (2)

где 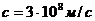- скорость распространения электромагнитной волны в вакууме; T – период колебания.

Колебательный контур настроен на электромагнитную волну, следовательно, собственная частота колебаний контура должна совпадать с частотой электромагнитной волны, поэтому период электромагнитных колебаний в контуре должен быть равен периоду колебаний электромагнитной волны.

По формуле Томсона период колебаний в контуре

. (3)

Из (1) имеем:

. (4)

Подставим выражение (4) в формулу (3), получим:

.

Подставим выражение (5) в формулу (2), получим:

. (6)

Из формулы (6) выразим величину максимального заряда на пластинах конденсатора:

.

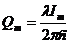Проверка размерности расчетной формулы:

.

Вычисление:

.

Ответ: максимальный заряд на пластинах конденсатора равен .

Не нашли, что искали? Воспользуйтесь поиском: