Примеры решения задач. Задача 1.Длина волны, на которую приходится максимум энергии в спектре излучения черного тела 0,58 мкм

Задача 1. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела 0,58 мкм. Определить энергетическую светимость (излучательность) поверхности тела.

Дано:

______________________

Решение.

Энергетическая светимость R_e абсолютно черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой степени термодинамической температуры и выражается формулой

, (1)

где - постоянная Стефана-Больцмана, Т - термодинамическая температура.

Температуру Т можно вычислить с помощью закона Вина:

, (2)

где b - постоянная первого закона смещения Вина.

Используя формулы (2) и (1), получаем выражение:

(3)

.

Произведем вычисления:

.

Ответ: энергетическая светимость поверхности тела равна .

Задача 2. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра:

1) ультрафиолетовым излучением с длиной волны 0,155 мкм;

2) гамма-излучением с длиной волны 1 пм.

Дано: ,

_.

___________________________

Решение.

Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта

, (1)

где  - энергия фотонов, падающих на поверхность металла,

А - работа выхода электрона,

- максимальная кинетическая энергия фотоэлектронов.

Энергия фотона вычисляется также по формуле:

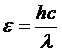, (2)

где h - постоянная Планка, с - скорость света в вакууме, 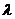- длина световой волны.

Кинетическая энергия электрона может быть выражена или по классической формуле:

(3)

или по релятивистской формуле:

, (4)

где E_o - энергия покоя электрона, .

Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект. Если энергия фотона намного меньше энергии покоя E_o электрона, то может быть применена формула (3). Если же ’энергия фотона сравнима по величине с энергией покоя электрона E_o, то вычисление по формуле (3) приводит к большой ошибке, поэтому нужно пользоваться формулой (4).

1) Вычислим энергию фотона ультрафиолетового излучения по формуле (2):

или

.

Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (0,51 МэВ). Следовательно, в этом случае кинетическая энергия фотоэлектронов в формуле (1) может быть выражена по классической формуле (3):

,

Откуда

. (5)

Проверим размерность выражения (5).

.

Подставим значение величин в формулу (5):

2) Вычислим энергию фотона гамма-излучения:

или во внесистемных единицах:

Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона ( ₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует использовать релятивистскую формулу кинетической энергии (4).

Из этой формулы

Заметив, что и , получим:

.

Энергии Е_о и ₂ входят расчетную формулу в виде отношения, поэтому их можно выражать во внесистемных единицах.

Вычисление:

Ответ: максимальная скорость фотоэлектронов, вырываемых с поверхности серебра ультрафиолетовым излучением, равна ;

максимальная скорость фотоэлектронов, вырываемых с поверхности серебра гамма-излучением, равна

Задача 3. Фотон с энергией ε = 0,75МэВ рассеялся на свободном электроне под углом θ = 60°. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определить: 1) энергию рассеянного фотона; 2) кинетическую энергию Т электрона отдачи; 3) направление его движения.

Дано:

θ = 60°.

___________________________________

T -?

Решение.

1. Энергию рассеянного фотона найдем, воспользовавшись формулой Комптона:

, (1)

где 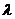- длина волны падающего фотона;

- длина волны рассеянного фотона;

- масса покоя электрона;

- скорость света в вакууме;

- угол рассеяния фотона.

Выразив длины волн λ' и λ через энергии ε ', рассеянного фотона, и ε, падающего фотона, получим:

. (2)

Приведем выражение (2) к виду

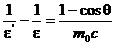. (3)

Известно, что энергия покоя электрона

(формула Эйнштейна) (4)

С учетом (4) формулу (3) запишем в виде:

. (5)

Подставив числовые значения величин, получим значение энергии рассеянного фотона:

ε ' = 0,43 МэВ.

2. Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией падающего фотона

и энергией рассеянного фотона:

. (6)

3. Направление движения электрона отдачи найдем, применив закон сохранения импульса, согласно которому импульс падающего фотона P равен векторной сумме импульсов рассеянного фотона и электрона отдачи.

, (7)

где - импульс падающего фотона;
- импульс рассеянного фотона;

- импульс электрона отдачи.

Векторная диаграмма импульсов изображена на рисунке. Все векторы проведены из точки О, где находился электрон в момент соударения с фотоном. Угол φ определяет направление движения электрона отдачи.

Из треугольника OCD находим

, (8)

или

. (9)

Так как и , то

. (10)

Преобразуем формулу (10) так, чтобы угол φ выражался непосредственно через величины ε и θ, заданные в условии задачи. Из формулы (3) следует:

. (11)

C учетом (5) формула (10) примет вид:

. (12)

Учитывая, что и после соответствующих преобразований получим:

. (13)

После вычисления по формуле (13) найдем , откуда φ = 35°.

Ответ: энергия рассеянного фотона равна 0,43 МэВ; кинетическая энергия электрона отдачи равна 0,32 МэВ; направление движения электрона отдачи определяется углом φ, равным 35°.

Задача 4. Пучок монохроматического света с длиной волны 663 нм падает нормально на зеркальную плоскую поверхность. Поток энергии равен0,6 Вт. Определить силу F давления, испытываемую этой поверхностью, а также число N фотонов, падающих на нее за время, равное 5 с.

Дано:

___________________

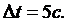
F -? N -?

Решение.

Сила светового давления на поверхность равна произведению светового давления P на площадь S поверхности:

. (1)

Световое давление может быть найдено по формуле

, (2)

где - облученность поверхности (энергия всех фотонов, падающих на поверхности за 1 с;

- коэффициент отражения (для зеркальной поверхности ).

- скорость света в вакууме.

Подставляя выражение (2) давления света в формулу (1), получим:

. (3)

Так как произведение облученности на площадь поверхности равно потоку энергии излучения, падающего на поверхность, то соотношение (3) можно записать в виде:

, (4)

где - поток энергии излучения.

Производим вычисления:

.

Число фотонов, падающих за время на поверхность, определяется по формуле:

, (5)

где - энергия излучения, получаемая поверхностью за время ;

- энергия фотона.

Выразив в формуле (5) энергию фотона через длину волны , получим:

. (6)

Подставив в формулу (6) числовые значения величин и произведя вычисления, получим:

(фотонов)

Ответ: сила давления, испытываемая поверхностью, равна ;

за пять секунд на поверхность падает фотонов.

Не нашли, что искали? Воспользуйтесь поиском: