ПРАКТИЧНЕ ЗАНЯТТЯ №2

Тема: Рівняння прямої в просторі.

Мета: Засвоїти різні способи задання прямих в просторі та навчитися використовувати їх для розв’язку задач.

План

1. Способи задання прямих та зміст параметрів, що входять в рівняння.

2. Відстань від точки до прямої.

3. Кут між прямими та умови їх паралельності, перпендикулярності.

4. Самостійна робота.

Завдання 1. Побудувати пряму, що задається рівнянням:

.

Розв’язок. Для побудови прямої знайдемо її точки перетину з координатними площинами.

Пл. : , , , , .

Пл. : , , , , .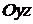

Пл. : , , , , .

Візьмемо будь-які дві точки, наприклад , .

Завдання 2. Скласти рівняння прямої, що проходить через дві точки: , .

Розв’язок. Використаємо рівняння прямої, що проходить через дві точки:

.

Підставляючи координати точок , , отримаємо

,

.

Відповідь: .

Завдання 3. Представити рівняння прямої в канонічному виді.

Розв’язок. Канонічним являється рівняння прямої:

,

де – точка, що лежить на прямій, – напрямний вектор прямої.

Кожне з рівнянь в заданому загальному рівнянні прямої характеризує площину.

,

,

Векторний добуток двох векторів , дає напрямний вектор:

,

, , .

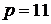Для визначення координат точки, що лежить на прямій, зафіксуємо одну координату. Нехай , тоді

(помножуючи друге рівняння на 3 та додаючи до першого)

,

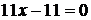З рівняння при знаходимо . Тобто, маємо точку і канонічне рівняння має вид:

.

Відповідь: .

Завдання 4. Скласти рівняння прямої що проходить через точку паралельно прямій

Розв’язок. Знайдемо рівняння прямої в канонічному виді

.

Оскільки шукана пряма проходить паралельно заданій, то їх напрямні вектори співпадають

.

Отже шукане рівняння прямої:

.

Відповідь: .

Завдання 5. Знайти відстань від точки до прямої .

Розв’язок. Із даного рівняння прямої маємо координати точки , що належить прямій та координати напрямного вектора прямої .

Шукана відстань являється висотою паралелограма. Враховуючи, що площу паралелограма можна обчислити двояко, тобто:

або ,

,

де .

,

,

.

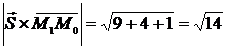Відповідь: од.

Завдання 6. Знайти кут між прямими:

,

.

Розв’язок. Кут між прямими визначається як кут між їх напрямними векторами , . В нашому випадку , .

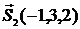Отримаємо:

,

.

Відповідь: .

Самостійна робота:

1. Побудувати пряму .

2. Представити рівняння прямої в канонічному виді

3. Скласти рівняння сторін трикутника з вершинами , , .

4. З’ясувати взаємне положення прямих

а) паралельні,

б) перпендикулярні,

в) не паралельні и не перпендикулярні,

1) , ,

2) , .

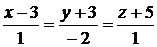Типові завдання (з коментарем)

Завдання 1. Знайти координати точок перетину прямих

а) , б) ,

з площинами , .

Не нашли, что искали? Воспользуйтесь поиском: