ПРАКТИЧНЕ ЗАНЯТТЯ №3

Тема: Пряма та площина в просторі.

Мета: Формування вмінь та навиків при розв’язуванні сумісних задач з використанням понять: прямої та площини.

План

1. Взаємне розташування прямої та площини.

2. Визначення координат точки перетину прямої і площини та кута між ними.

3. Умови паралельності та перпендикулярності прямої і площини.

4. Самостійна робота.

Завдання 1. Скласти рівняння прямої, що проходить через точку перпендикулярно до площини .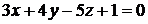

Розв’язок.

Оскільки пряма проходить перпендикулярно до площини, то напрямний вектор прямої буде співпадати з нормальним вектором площини. В нашому випадку , тому канонічне рівняння прямої матиме вид:

.

Відповідь: .

Завдання 2. Визначити координати точок перетину прямої і площини та кут між ними:

,

.

Розв’язок. Представимо рівняння прямої в параметричному виді

,

, , .

Підставимо отримані рівняння в рівняння площини

,

,

, .

Отже

, , ,

, , .

Враховуючи, що кут між прямою та площиною визначається як кут між напрямним вектором прямої та нормальним вектором площини , отримаємо

,

.

Відповідь: точка перетину , кут .

Завдання 3. Довести, що пряма лежить на площині .

Розв’язок. Якщо пряма лежить на площині, то повинні виконуватися дві умови:

1. пряма паралельна площині, тобто ;

2. точка, що лежить на прямій повинна лежати і на площині.

Оскільки , та точка лежить на прямій, отримаємо

1. ;

2. .

Отже пряма належить площині.

Самостійна робота:

1. З’ясувати взаємне розміщення прямої та площини:

а) паралельні,

б) перпендикулярні,

в) не паралельні и не перпендикулярні,

, ,

, .

2. Скласти рівняння площини, що проходить через точку перпендикулярно до прямої .

Типові завдання (з коментарем)

Завдання 1. Показати, що пряма паралельна площині .

Розв’язок. Якщо площина і пряма паралельні, то напрямній вектор прямої повинен бути перпендикулярним до нормального вектора площини . Тобто їх скалярний добуток дорівнює нулю:

, пряма паралельна площині.

Завдання 2. Показати, що пряма лежить на площині .

Розв’язок. Якщо дана пряма лежить на вказаній площині, то система повинна мати нескінченну кількість розв’язків. Виразимо кожну змінну прямої через параметр:

Підставляючи в рівняння площини попередні рівності, отримаємо

, ,

для будь-якого параметра виконується рівність. Тобто можна вказати нескінченну кількість точок які одночасно знаходяться на прямій та площині, отже пряма лежить на площині.

Завдання 3. Скласти рівняння площини, що проходить через пряму і точку .

Розв’язок. Нехай точка належить шуканій площині. Розглянемо також точку , яка прямій. Тоді напрямний вектор прямої та вектори , компланарні, тобто їх змішаний добуток дорівнює повинен дорівнювати нулю:

,

.

Відповідь: .

Не нашли, что искали? Воспользуйтесь поиском: