Условия параллельности и перпендикулярности двух прямых

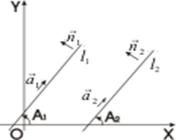
Пусть заданы прямые l ₁ и l ₂. своими общими уравненими; 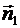= (А₁,B₁), 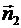= (А₂,В₂) – нормальные векторы этих прямых; k ₁ = tgα₁, k ₂ = tgα₂ – угловые коэффициенты; = (m ₁, n ₁), 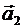(m ₂, n ₂) – направляющие векторы. Тогда, прямые l ₁ и l ₂ параллельны, в том и только том случае, если выполняется одно из следующих условий:

либо 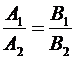, либо k ₁= k ₂, либо .

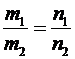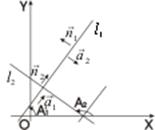Пусть теперь прямые l ₁ и l ₂ перпендикулярны. Тогда, очевидно, , то есть А₁А₂ + В₁В₂ = 0.

Если прямые l ₁ и l ₂ заданы соответственно уравнениями

l ₁: у = k ₁ x + b ₁,

l ₂: у = k ₂ x + b ₂,

то tgα₂ = tg(90º+α) = .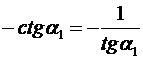

Отсюда следует, что

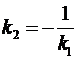
Наконец, если и 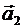направляющие векторы прямых, то ^ 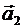, то есть

m ₁ m ₂ + n ₁ n ₂ = 0

Последнее соотношение выражает необходимое и достаточное условие перпендикулярности двух прямых.

Не нашли, что искали? Воспользуйтесь поиском: