Общее уравнение прямой. Уравнение прямой в отрезках.

Пусть задана некоторая афинная система координат OXY.

Теорема. Любая прямая l системе координат ОX задается линейным уравнением вида

А x + B y + С = О, (1)

где А, В, С R и А² + В² 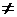0. Обратно, любое уравнение вида (1) задает прямую.

Уравнение вида (1) - общее уравнение прямой.

Пусть в уравнении (1) все коэффициенты А, В и С отличны от нуля. Тогда

-Ах-By=-С, и .

Обозначим -С/А=а, -С/B=b. Получим

- уравнение в отрезках.

Действительно, числа |а| и |b| указывают на величины отрезков, отсекаемых прямой l на осях ОХ и OY соответственно.

Пусть прямая l задана общим уравнением (1) в прямоугольной системе координат и пусть точки M₁(x₁,у₁) и М₂(х₂,у₂) принадлежит l. Тогда

А x ₁ + В у ₁ + С = А х ₂ + В у ₂ + С, то есть A(x ₁- x ₂) + В(у ₁- у ₂) = 0.

Последнее равенство означает, что вектор =(А,В) ортогонален вектору =(x₁-x₂,у₁-у₂). т.е. Вектор (А,В) называется нормальным вектором прямой l.

Рассмотрим вектор =(-В,А). Тогда

=А(-В)+ВА=0. т.е. ^ .

Следовательно, вектор =(-В,А) является направляющим вектором пряной l.

Не нашли, что искали? Воспользуйтесь поиском: